Idempotente matrix

Op deze pagina leggen we uit wat idempotente matrices zijn. We laten u ook verschillende voorbeelden van dit soort matrices zien, zodat u het volledig begrijpt. Ook vindt u de formule om een idempotente matrix te vinden en, ten slotte, alle eigenschappen van idempotente matrices.

Wat is een idempotente matrix?

De definitie van een idempotente matrix is als volgt:

Een idempotente matrix is die matrix die, vermenigvuldigd met zichzelf, dezelfde matrix als resultaat oplevert.

$A\cdot A = A$

Daarom is elke macht van een idempotente matrix gelijk aan de matrix zelf, ongeacht de exponent:

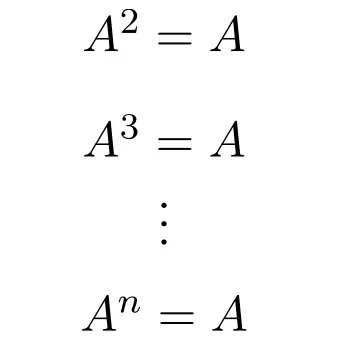
Dit is eigenlijk de reden waarom dit type bord zijn naam heeft gekregen. Omdat in de wiskunde idempotentie een operatie is, wat betekent dat we altijd hetzelfde resultaat verkrijgen, ongeacht hoe vaak het wordt uitgevoerd.

Voorbeelden van idempotente matrices

Zodra we het concept van de idempotente matrix kennen, zullen we enkele voorbeelden van verschillende dimensies zien om het begrip ervan te voltooien.

Voorbeeld van 2 × 2 idempotente matrix

De volgende vierkante matrix met afmeting 2×2 is idempotent:

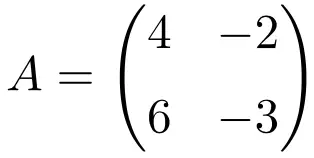
voorbeeld van een idempotente matrix met dimensie 2x2

Om te verifiëren dat het een idempotente matrix is, berekenen we het kwadraat ervan:

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Het resultaat is identiek, we laten daarom zien dat het een idempotente matrix is.

Voorbeeld van een 3×3 idempotente matrix

De volgende vierkante matrix van maat 3×3 is idempotent:

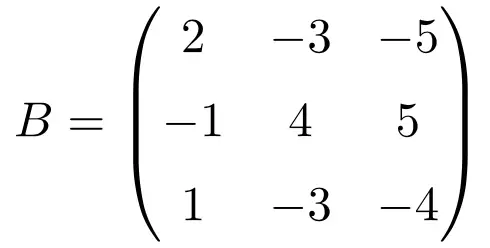
voorbeeld van een idempotente matrix met dimensie 3x3

Om te controleren of een idempotente matrix overeenkomt, verhogen we de matrix naar 2:

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Het resultaat is hetzelfde als de originele matrix, dus de idempotentie van de matrix is bewezen.

Structuur van een 2×2 idempotente matrix

Hier laten we u de formule zien om een idempotente matrix te verkrijgen. Als je meer geïnteresseerd bent, kun je de demonstratie van de formule hieronder in de reacties zien, maar het is een beetje vervelend, dus laten we je hier direct achter met de formule voor idempotente matrices :

Op zo’n manier dat de elementen van de secundaire diagonaal van een idempotente matrix willekeurig kunnen zijn zolang aan de voorwaarde wordt voldaan

$a^2+bc=a$

en de cijfers op de hoofddiagonaal moeten zijn

$a$

$1-a.$

Naast alle matrices die door deze formule worden beschreven, moeten we de Identiteitsmatrix toevoegen, die ook een idempotente matrix is, hoewel deze de formule niet respecteert. Als u niet weet wat de array is, kunt u vragen wat de Identity-array is .

Eigenschappen van idempotente matrices

Idempotente matrices hebben de volgende kenmerken:

De determinant van een idempotente matrix is altijd 0 of 1.

Met uitzondering van de identiteitsmatrix zijn alle andere idempotente matrices zowel enkelvoudige als gedegenereerde matrices, dat wil zeggen dat ze niet inverteerbaar zijn.

Elke idempotente matrix is diagonaliseerbaar en de eigenwaarden (of eigenwaarden) ervan zijn altijd 0 of 1.

Het spoor van een idempotente matrix is gelijk aan de rangorde van de matrix.

Tenslotte bestaat er een relatie tussen idempotente matrices en involutionele matrices: de matrix
$A$

is idempotent als en slechts als de matrix

$\displaystyle P= 2A-I$

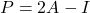
het is involutioneel.