Regelmatige of inverteerbare matrix

Op deze pagina vindt u de uitleg van een reguliere of inverteerbare matrix en hoe u weet wanneer de inversie van een matrix kan worden uitgevoerd en wanneer niet. Daarnaast zul je ook verschillende voorbeelden van reguliere matrices zien om het concept volledig te begrijpen en tot slot zullen we je alle eigenschappen van dit type matrix laten zien.

Wat is een reguliere matrix?

De definitie van een reguliere matrix is als volgt:

Een reguliere matrix is een vierkante matrix die kan worden geïnverteerd, dat wil zeggen dat de inverse van genoemde matrix kan worden berekend. Daarom is de determinant ervan niet nul (0).

Reguliere matrices worden ook wel inverteerbare, niet-singuliere of niet-gedegenereerde matrices genoemd.

De tegenovergestelde matrix van de reguliere matrix is de enkelvoudige of gedegenereerde matrix.

Om dus te weten wanneer een matrix regelmatig of enkelvoudig is, dat wil zeggen wanneer een matrix inverteerbaar is of niet, volstaat het om de determinant van de matrix op te lossen:

Als de determinant van de matrix niet nul is, is de matrix regelmatig of inverteerbaar.

Als de determinant van de matrix gelijk is aan nul, is de matrix singulier of niet inverteerbaar.

Concluderend is het berekenen van de determinant van een matrix de eenvoudigste manier om te weten of de matrix een inverse heeft of niet, dus dit is wat we aanbevelen voor het bepalen van de invertibiliteit van elke matrix.

Als je wilt weten hoe je een matrix moet omkeren, kun je de inverse matrixformule bekijken, waarin stap voor stap wordt uitgelegd hoe je een matrix moet omkeren. Je vindt er ook verschillende voorbeelden en opgeloste oefeningen om te oefenen.

Voorbeelden van reguliere of inverteerbare matrices

Nadat we de betekenis van een reguliere of inverteerbare matrix hebben gezien, gaan we enkele voorbeelden bekijken van reguliere matrices met verschillende dimensies:

Voorbeeld van een reguliere of inverteerbare 2×2 matrix

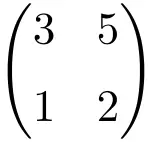
We kunnen verifiëren dat het een reguliere matrix is door de determinant ervan te berekenen:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

De determinant van de orde 2-matrix is anders dan 0, dus het is een reguliere matrix.

Voorbeeld van een reguliere of inverteerbare 3×3-matrix

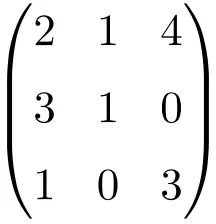
voorbeeld van een regelmatige of inverteerbare matrix met dimensie 3x3

We moeten de determinant van de matrix maken om te verifiëren dat het een inverteerbare matrix is:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

De determinant van de matrix van orde 3 geeft een ander resultaat dan 0, dus het is een reguliere matrix.

Voorbeeld van een reguliere of inverteerbare 4×4-matrix

voorbeeld van een regelmatige of inverteerbare matrix met dimensie 4x4

Als we de determinant van de matrix nemen, blijkt dat het een reguliere matrix is:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

De determinant van de matrix van orde 4 is niet nul, het is daarom een inverteerbare matrix.

Waarschuwing: Als u twijfels heeft over de berekeningen van determinanten, kunt u de pagina Hoe berekent u een determinant raadplegen?

Eigenschappen van reguliere of inverteerbare matrices

Reguliere of inverteerbare matrices zijn erg belangrijk voor lineaire algebra, en dit komt door de volgende kenmerken:

Als A een inverteerbare matrix is, is de getransponeerde of getransponeerde matrix dat ook. Bovendien is de inverse matrix van de getransponeerde gelijk aan de getransponeerde van de inverse.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

Het bereik van een reguliere matrix is altijd het maximaal mogelijke, of met andere woorden, het bereik is gelijk aan de dimensie van de matrix.

Het matrixproduct tussen twee inverteerbare matrices geeft aanleiding tot een andere reguliere matrix. Deze voorwaarde kan eenvoudig worden aangetoond met de eigenschappen van de determinanten:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Elke orthogonale matrix is tegelijkertijd een reguliere matrix.

Laat A de matrix zijn die een systeem van lineaire vergelijkingen vertegenwoordigt
$(Ax=b)$

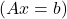
Als A een reguliere matrix is, heeft het systeem een unieke oplossing en is het daarom een compatibel determinantensysteem (SCD).

Bovendien, als het systeem een homogeen systeem is
$(Ax=0)$

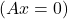
en A kan worden omgekeerd, de oplossing van het systeem is triviaal:

$x=0.$

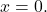
De kolommen en rijen van een reguliere matrix zijn lineair onafhankelijk van elkaar.

Alle eigenwaarden (of eigenwaarden) van een reguliere of inverteerbare matrix zijn niet nul.

Regelmatige gouden inverteerbare matrix