Antisymmetrische matrix

Op deze pagina leggen we uit wat antisymmetrische matrices zijn. Bovendien zult u verschillende voorbeelden en de typische structuur ervan kunnen zien om het perfect te begrijpen. We leggen ook de bijzonderheid uit van het berekenen van de determinant van een antisymmetrische matrix en alle eigenschappen van dit type matrix. En ten slotte zul je ontdekken hoe je elke vierkante matrix kunt ontbinden in de som van een symmetrische matrix plus een andere antisymmetrische matrix.

Wat is een antisymmetrische matrix?

De definitie van antisymmetrische matrix is als volgt:

Een antisymmetrische matrix is een vierkante matrix waarvan de transpositie gelijk is aan het negatief van de matrix.

$A^t = -A$

Goud

$A^t$

vertegenwoordigt de getransponeerde matrix van

$A$

$-A$

is de matrix

$A$

met al zijn elementen van teken veranderd.

Voorbeelden van antisymmetrische matrices

Zodra we het concept van antisymmetrische matrix kennen, zullen we verschillende voorbeelden van antisymmetrische matrices zien om het beter te begrijpen:

Voorbeeld van een antisymmetrische matrix van orde 2 × 2

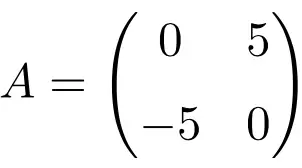
voorbeeld van een antisymmetrische matrix met dimensie 2x2

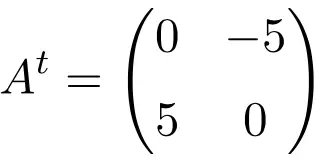
opgeloste oefening van antisymmetrische matrix van dimensie 2x2

Voorbeeld van een antisymmetrische matrix met afmeting 3×3

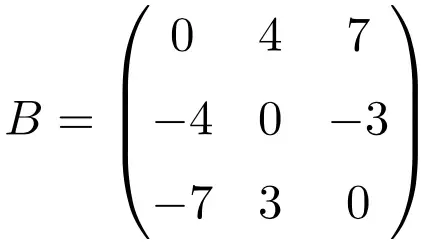
voorbeeld van een antisymmetrische matrix met dimensie 3x3

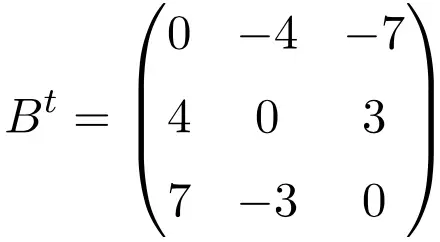
opgeloste oefening van antisymmetrische matrix van dimensie 3x3

Voorbeeld van een antisymmetrische matrix van maat 4×4

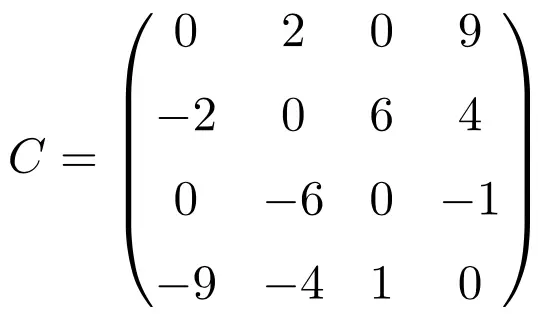
voorbeeld van een antisymmetrische matrix met dimensie 4x4

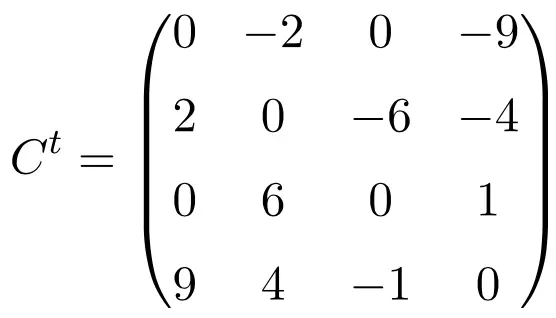
opgeloste oefening van antisymmetrische matrix van dimensie 4x4

Bij het transponeren van deze drie matrices verifiëren we dat ze antisymmetrisch zijn, omdat de getransponeerde matrices equivalent zijn aan hun respectieve originele matrices met een verandering van teken.

Structuur van een antisymmetrische matrix

Om aan de antisymmetrische matrixvoorwaarde te voldoen, moeten ze altijd hetzelfde type structuur hebben: de getallen op de hoofddiagonaal zijn allemaal gelijk aan nul en het element van rij i en kolom j is het negatief van het element van rij j en kolom ik . Met andere woorden, de vorm van de antisymmetrische matrices is als volgt:

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

Daarom fungeert de hoofddiagonaal van een antisymmetrische matrix als de as van antisymmetrie. Dit is waar de naam van deze specifieke matrix vandaan komt.

Determinant van een antisymmetrische matrix

De determinant van een antisymmetrische matrix hangt af van de dimensie van deze matrix. Dit komt door de eigenschappen van de determinanten:

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

Dus als de antisymmetrische matrix van een oneven orde is, zal de determinant ervan gelijk zijn aan 0 . Aan de andere kant, als de antisymmetrische matrix een gelijke dimensie heeft, kan de determinant elke waarde aannemen.

Daarom is een antisymmetrische matrix met een oneven dimensie een enkelvoudige of gedegenereerde matrix. Aan de andere kant is een antisymmetrische matrix van gelijke orde een reguliere matrix.

Eigenschappen van antisymmetrische matrices

De kenmerken van antisymmetrische matrices zijn als volgt:

Het optellen (of aftrekken) van twee antisymmetrische matrices levert nog een antisymmetrische matrix op. Omdat het transponeren van twee opgetelde (of afgetrokken) matrices gelijk staat aan het afzonderlijk transponeren van elke matrix:

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

Elke antisymmetrische matrix vermenigvuldigd met een scalair geeft ook aanleiding tot een andere antisymmetrische matrix.

De kracht van een antisymmetrische matrix is gelijkwaardig aan een antisymmetrische matrix of een symmetrische matrix. Als de exponent een even getal is, is het machtsresultaat een symmetrische matrix, maar als de exponent een oneven getal is, is het machtsresultaat een antisymmetrische matrix. Je kunt in deze link raadplegen wat een symmetrische matrix is .

Het spoor van een antisymmetrische matrix is altijd gelijk aan nul.

De som van elke antisymmetrische matrix plus de unitaire matrix geeft aanleiding tot een inverteerbare matrix.

$\displaystyle \text{det}(A+I)\neq 0$

Alle reële eigenwaarden (of eigenwaarden) van een antisymmetrische matrix zijn 0. Een antisymmetrische matrix kan echter ook complexe eigenwaarden hebben.

Alle antisymmetrische matrices zijn normale matrices. Daarom zijn ze onderworpen aan de spectrale stelling, die zegt dat een antisymmetrische matrix gediagonaliseerd kan worden door een unitaire matrix.

Ontleding van een vierkante matrix in een symmetrische matrix en een antisymmetrische matrix

Een speciaal kenmerk van vierkante matrices is dat ze kunnen worden ontleed in de som van een symmetrische matrix plus een antisymmetrische matrix.

De formule waarmee we dit kunnen doen is als volgt:

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

Waar C de vierkante matrix is die we willen ontleden, ^wordt C getransponeerd, en tenslotte zijn S en A respectievelijk de symmetrische en antisymmetrische matrices waarin de matrix C wordt ontleed.

Hieronder vindt u een opgeloste oefening om de formule te demonstreren. Laten we de volgende matrix ontleden:

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

We berekenen de symmetrische en antisymmetrische matrix met de formules:

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

En we kunnen controleren of aan de vergelijking is voldaan door de twee matrices op te tellen:

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅