Orthogonale matrix

Op deze pagina zie je wat orthogonale matrices zijn en welke relatie ze hebben met de inverse van een matrix. Je zult ook verschillende voorbeelden zien om het perfect te begrijpen. Daarnaast leren we je de formule die elke orthogonale matrix controleert, waarmee je er snel een weet te vinden. En tot slot vindt u de eigenschappen en toepassingen van deze specifieke matrices, evenals een typische opgeloste examenoefening.

Wat is een orthogonale matrix?

De definitie van orthogonale matrix is als volgt:

Een orthogonale matrix is een vierkante reële getallenmatrix die vermenigvuldigd met zijn transponering (of transponering) gelijk is aan de identiteitsmatrix. Dat wil zeggen dat aan de volgende voorwaarde is voldaan:

$A\cdot A^t = A^t \cdot A =I$

Goud

$A$

is een orthogonale matrix en

$A^t$

vertegenwoordigt de getransponeerde matrix.

Om aan deze voorwaarde te voldoen, moeten de kolommen en rijen van een orthogonale matrix orthogonale eenheidsvectoren zijn, dat wil zeggen dat ze een orthonormale basis moeten vormen. Om deze reden noemen sommige wiskundigen ze ook orthonormale matrices .

Inverse van een orthogonale matrix

Een andere manier om het concept van een orthogonale matrix uit te leggen is via de inverse matrix, omdat de getransponeerde (of getransponeerde) matrix van een orthogonale matrix gelijk is aan zijn inverse.

Om deze stelling volledig te begrijpen, is het belangrijk dat je weet hoe je een matrix moet omkeren . In deze link vind je een gedetailleerde uitleg van de inverse van een matrix, al zijn eigenschappen en heb je zelfs stap-voor-stap opgeloste oefeningen om te oefenen.

Met behulp van de orthogonale matrixvoorwaarde en de belangrijkste eigenschap van inverse matrices kan gemakkelijk worden aangetoond dat de inverse matrix van een orthogonale matrix equivalent is aan de transponering ervan:

$\left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}$

Daarom zal een orthogonale matrix altijd een inverteerbare matrix zijn, of met andere woorden, het zal een reguliere of niet-gedegenereerde matrix zijn.

Vervolgens zullen we verschillende voorbeelden van orthogonale matrices zien om het concept van alles te begrijpen.

Voorbeeld van een 2×2 orthogonale matrix

De volgende matrix is een orthogonale matrix met afmeting 2×2:

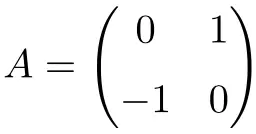
We kunnen controleren of het orthogonaal is door het product te berekenen door middel van zijn transpositie:

$\displaystyle A\cdot A^t$

$\displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Omdat het resultaat de identieke matrix oplevert, verifiëren we dat A een orthogonale matrix is.

Voorbeeld van een 3×3 orthogonale matrix

De volgende matrix is een orthogonale matrix met afmeting 3×3:

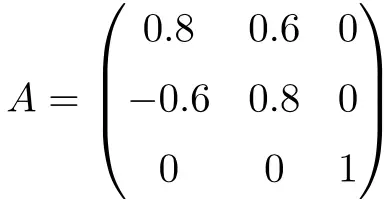
We kunnen aantonen dat het orthogonaal is door de matrix A te vermenigvuldigen met zijn transpositie:

$\displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}$

Omdat de oplossing de unitaire matrix is, laten we zien dat A een orthogonale matrix is.

Formule voor het vinden van een 2×2 orthogonale matrix

We zullen dan het bewijs zien dat alle orthogonale matrices van orde 2 hetzelfde patroon volgen.

Beschouw een generieke matrix van maat 2×2:

$\displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}$

Om deze matrix orthogonaal te laten zijn, moet aan de volgende matrixvergelijking worden voldaan:

$\displaystyle A\cdot A^t =I$

$\displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Door de matrixvermenigvuldiging op te lossen, verkrijgen we de volgende vergelijkingen:

$\displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}$

Als je goed kijkt, lijken deze gelijkheden veel op de fundamentele trigonometrische relatie van Pythagoras :

$\displaystyle \sin ^2\alpha+\cos ^2\alpha=1$

Bijgevolg zijn de verkregen termen die voldoen aan de vergelijkingen (1) en (3):

$\displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}$

Door de waarden in de tweede vergelijking te vervangen, verkrijgen we bovendien de relatie tussen de twee hoeken:

$\displaystyle ac+bd=0$

$\displaystyle \cos\theta\sin\phi+\sin\theta\cos\phi=0$

$\displaystyle \tan\phi=-\tan\theta$

Dat wil zeggen dat aan een van de volgende twee voorwaarden moet worden voldaan:

$\displaystyle \text{si} \quad c=\sin\phi=-\sin\theta \quad \longrightarrow \quad d=\cos\phi=\cos\theta$

$\displaystyle \text{si} \quad d=\cos \phi=-\cos \theta \quad \longrightarrow \quad c=\sin\phi=\sin\theta$

Kortom, orthogonale matrices moeten de structuur hebben van een van de volgende twee matrices:

formule voor de orthogonale matrix van dimensie 2x2

Goud

$\theta$

is een reëel getal.

Als we bijvoorbeeld de waarde toekennen

$\displaystyle\theta=\frac{\pi}{2}$

en we nemen de eerste structuur, we verkrijgen de matrix waarvan we hebben geverifieerd dat deze orthogonaal is in de sectie “Voorbeeld van 2×2 orthogonale matrix”:

$\displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}$

Orthogonale matrixeigenschappen

De kenmerken van dit type matrix zijn:

Een orthogonale matrix kan nooit een singuliere matrix zijn, omdat deze altijd geïnverteerd kan worden. In deze zin is de inverse van een orthogonale matrix een andere orthogonale matrix.

Elke orthogonale matrix kan worden gediagonaliseerd. We zeggen dan dat orthogonale matrices orthogonaal diagonaliseerbaar zijn.

Alle eigenwaarden of eigenwaarden van een orthogonale matrix hebben een modulus gelijk aan 1.

Elke orthogonale matrix die alleen uit reële getallen bestaat, is ook een normale matrix.

Het analogon van de orthogonale matrix in een omgeving met complexe getallen is de unitaire matrix.

Het is duidelijk dat de identiteitsmatrix een orthogonale matrix is.

De verzameling orthogonale matrices met dimensie n × n en de werking van het matrixproduct vormen een groep die orthogonale groep wordt genoemd. Dat wil zeggen dat het product van twee orthogonale matrices gelijk is aan een andere orthogonale matrix.

Bovendien kan het resultaat van het vermenigvuldigen van een orthogonale matrix met zijn transpositie worden uitgedrukt door de Kronecker-delta:

$\displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}$

Tenslotte is de determinant van een orthogonale matrix altijd +1 of -1.

$\displaystyle \text{det}(A)=\pm 1$

Opgeloste oefening van orthogonale matrices

Vervolgens lossen we een oefening op orthogonale matrices op.

Gegeven de volgende vierkante matrix van orde 3, zoek de waarden van
$a$

En

$b$

om het orthogonaal te maken:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}$

Om aan de orthogonaliteit van de matrix te voldoen, moet het product van de matrix door zijn transpositie gelijk zijn aan de identiteitsmatrix. DUS:

$\displaystyle A\cdot A^t = I$

$\displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}$

We vermenigvuldigen de matrices:

$\displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}$

We kunnen nu een vergelijking uit de linkerbovenhoek van de matrices halen, omdat de elementen op die positie moeten overeenkomen. Nog:

$\displaystyle \frac{1}{9}(2a^2+1) = 1$

We lossen de vergelijking op en elimineren het onbekende:

$\displaystyle 2a^2+1 = 9$

$\displaystyle 2a^2 = 8$

$\displaystyle a^2 = 4$

$\displaystyle \bm{a = \pm 2}$

Er zijn echter vergelijkingen die niet gelden voor de positieve oplossing, bijvoorbeeld die in de rechterbovenhoek. Alleen de negatieve oplossing is dus mogelijk .

Aan de andere kant, om de variabele te berekenen

$b$

we kunnen bijvoorbeeld de termen matchen die in de tweede rij van de eerste kolom zijn geplaatst:

$\displaystyle \frac{1}{9}(ab+a+b) = 0$

$\displaystyle ab+a+b = 0$

Door de waarde van te vervangen

$a$

in de vergelijking:

$\displaystyle -2b-2+b = 0$

$\displaystyle -b =2$

$\displaystyle \bm{b =-2}$

Kortom, de enige mogelijke oplossing is:

$\displaystyle \bm{a=b =-2}$

Dus de orthogonale matrix die overeenkomt met deze waarden is:

$\displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}$

Toepassingen van orthogonale matrices

Hoewel het misschien niet zo lijkt omdat ze meestal een heel eenvoudige vorm hebben, zijn orthogonale matrices erg belangrijk in de wiskunde, vooral op het gebied van lineaire algebra.

In de meetkunde vertegenwoordigen orthogonale matrices isometrische transformaties (die afstanden en hoeken niet veranderen) in echte vectorruimten. Daarom worden ze orthogonale transformaties genoemd. Bovendien zijn deze transformaties interne isomorfismen van de beschouwde vectorruimte. Deze transformaties kunnen rotaties , spiegelreflecties of inversies zijn.

Ten slotte wordt dit type matrix ook in de natuurkunde gebruikt, omdat hiermee de beweging van starre lichamen kan worden bestudeerd. En ze worden zelfs gebruikt bij het formuleren van bepaalde veldtheorieën.