Op deze pagina leggen we uit wat de factorstelling is. Daarnaast laten we zien waarvoor de factorstelling wordt gebruikt: deelbaarheid van veeltermen, wortels vinden, veeltermen in factoren ontbinden, enz. Ten slotte kun je oefenen met stapsgewijze oefeningen op de factorstelling.
Wat is de factorstelling?
In de wiskunde zegt de factorstelling dat een polynoom P(x) deelbaar is door een andere polynoom van de vorm (xa) dan en slechts dan als P(a)=0.
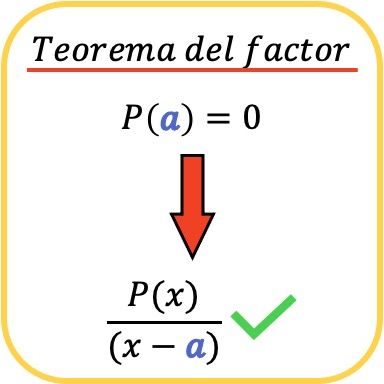
Op dezelfde manier volgt, als gevolg van de factorstelling, dat als een polynoom P(x) deelbaar is door de term (x−a), dit betekent dat de waarde a een wortel (of nul) is van de polynoom P( x). ).
Dat het ene polynoom deelbaar is door een ander betekent dat de rest (of rest) van de deling tussen de twee polynomen gelijk is aan nul. Mocht je dit concept niet helemaal onthouden, dan kun je in de volgende linkvoorbeelden zien van het delen van veeltermen , daar vind je ook de uitleg over het verdelen van veeltermen en oefeningen die stap voor stap worden opgelost.
Voorbeelden van factorstellingen
Nu we de wiskundige definitie van de factorstelling kennen, gaan we een aantal voorbeelden bekijken om te zien hoe deze wordt toegepast.
voorbeeld 1
Eén toepassing van de factorstelling is om erachter te komen of een gegeven polynoom deelbaar is door een binomiaal . Laten we een voorbeeld bekijken van hoe dit wordt gedaan met de factorstelling:
- Bepaal of de polynoom P(x) deelbaar is door de binomiale Q(x), waarbij beide zijn:
![]()
Ten eerste is het delerpolynoom, Q(x), een polynoom van het type (xa), dus we kunnen de factorstelling toepassen om het probleem op te lossen.
Om te controleren of P(x) kan worden gedeeld door Q(x), moeten we dus de numerieke waarde van de polynoom P(x) berekenen voor x=1, aangezien 1 de onafhankelijke term is van de delende polynoom waarvan het teken is veranderd. :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
De numerieke waarde van de polynoom P(x) bij x = 1 geeft nul, dus volgens de factorstelling is P(x) deelbaar door Q(x), of met andere woorden: de rest van de deling door beide zal nul zijn.
We kunnen verifiëren dat aan de deelbaarheidsvoorwaarde is voldaan door de 2 polynomen te delen door de stelling van Ruffini :
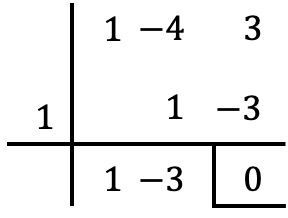
Zoals je in dit voorbeeld kunt zien, is de factorstelling een speciaal geval van de reststelling (of reststelling). Ik laat je dit artikel achter waarin wordt uitgelegd wat de reststelling is, je zult ook voorbeelden en oefeningen vinden die ermee zijn opgelost. En bovendien kun je zien wat het verschil is tussen de reststelling en de factorstelling.
Voorbeeld 2
De factorstelling kan ook worden gebruikt om de wortels (of nullen) van een polynoom te vinden. Maar om dit soort problemen te begrijpen, moet je uiteraard weten wat de wortels van een polynoom zijn . Als u dit concept nog steeds niet begrijpt, kunt u een kijkje nemen op de gelinkte pagina, die in detail wordt uitgelegd.
Laten we dus een voorbeeld bekijken hoe de factorstelling wordt toegepast om een wortel van een polynoom te vinden:
- Bereken, gegeven de polynoom P(x), of een van zijn wortels x=2 is:
![]()
Als we de factorstelling toepassen, zal de term x=2 alleen een wortel zijn van de polynoom P(x) als de numerieke waarde van P(x) voor x=2 nul is. We moeten dus deze numerieke waarde vinden:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
De numerieke waarde van de polynoom P(x) verdwijnt inderdaad bij x=2, dus dankzij de factorstelling kunnen we bevestigen dat x=2 een wortel is van de polynoom P(x).
Veeltermen in factoren ontbinden met behulp van de factorstelling
Een andere toepassing van de factorstelling is het ontbinden van polynomen . Voor het geval je niet weet wat het is: het factoriseren van een polynoom betekent het transformeren van de uitdrukking van een polynoom in een product van factoren, dat wil zeggen: het ontbinden van een polynoom vereenvoudigt de algebraïsche uitdrukking ervan.
De factorstelling stelt dus vast dat als een polynoom P(x) voldoet aan P(a)=0 voor een gegeven waarde a, de uitdrukking van genoemde polynoom kan worden ontbonden in het product P(x)=(xa) · Q( x), waarbij Q(x) het polynoom is dat ontstaat door het delen van het polynoom P(x) door (xa).
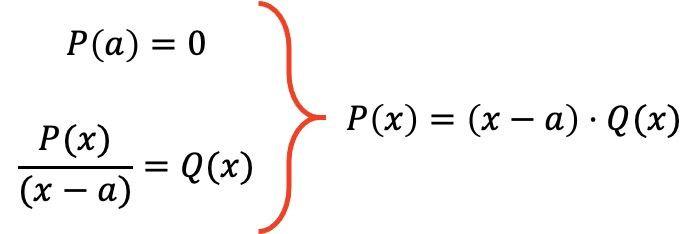
Als voorbeeld zullen we de volgende polynoom factoriseren met behulp van de faculteitsstelling:
![]()
Uit de vorige polynoom kunnen we weten dat x=-2 een van zijn wortels is, aangezien de numerieke waarde van de polynoom voor x=-2 gelijk is aan nul:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
We verdelen daarom met de regel van Ruffini de polynoom P(x) tussen de binominale gevormd door x en dit wortelveranderde teken, dat wil zeggen de factor (x+2):
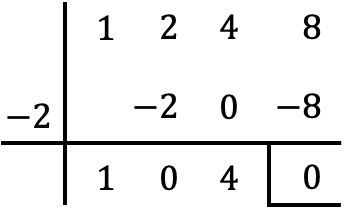
Het quotiënt van de polynomiale deling is dus:
![]()
En ten slotte kunnen we vanuit de factorstelling de polynoom P(x) uitdrukken in de vorm van een vermenigvuldiging van de factor (x+2) met het quotiënt verkregen in de vorige deling:
![]()
We hebben dus de polynoom P(x) ontbonden, maar slechts gedeeltelijk. Om een polynoom volledig in factoren te ontbinden, moet een langere procedure worden toegepast. We hebben een handleiding gemaakt waarin we stap voor stap leren hoe je Ruffini-polynomen kunt ontbinden . Daarnaast hebben we in dit artikel alle soorten ontbindingen uitgelegd en kun je oefenen met opgeloste oefeningen. Klik dus op de link om te zien hoe u een polynoom uit de verzameling kunt ontbinden.
Problemen met de factorstelling opgelost
Vervolgens hebben we verschillende oefeningen voorbereid die stap voor stap zijn opgelost met betrekking tot de factorstelling, zodat u kunt oefenen en zo kunt controleren of u deze stelling hebt begrepen. We raden u aan ze zelf te proberen en vervolgens te kijken of u de oplossing goed begrijpt. Vergeet ook niet dat u uw vragen hieronder in de reacties kunt achterlaten! ❓❓💬💬
Oefening 1
Gebruik de faculteitsstelling om te bepalen of de polynoom P(x) deelbaar is door de binomiale Q(x). Zo ja, zoek dan een wortel van de polynoom en ontbind deze in factoren.
![]()
In dit geval is de polynomiale deler Q(x) een binomiaal die alleen bestaat uit een x en een onafhankelijke term. Om dus aan te tonen dat de polynoom P(x) kan worden gedeeld door de andere polynoom Q(x) met de faculteitsstelling, moeten we de numerieke waarde van de polynoom P(x) evalueren in de onafhankelijke term van het delerpolynoom met veranderd teken, dat wil zeggen bij x=3:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
De numerieke waarde van de polynoom P(x) bij x=3 is equivalent aan 14, dat wil zeggen verschillend van nul. Volgens de factorstelling is P(x) dus NIET deelbaar door Q(x), omdat de rest van de deling niet nul is.
Oefening 2
Ontdek met de faculteitsstelling of de polynoom P(x) deelbaar is door de binomiale Q(x) en, zo ja, zoek een wortel van de polynoom P(x) en ontbind deze in factoren.
![]()
In dit geval is de polynoomdeler Q(x) een binomiaal die alleen bestaat uit een x en een onafhankelijke term, we kunnen daarom de faculteitsstelling toepassen.
En om te controleren of de polynoom P(x) kan worden gedeeld door de polynoom Q(x), moeten we de numerieke waarde van de polynoom P(x) vinden voor de onafhankelijke term van de polynoom Q(x) met een veranderd teken. dat wil zeggen, bij x=-1:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
In dit probleem is de numerieke waarde van de polynoom op x=-1 nul, dus P(x) is deelbaar door Q(x).
Vervolgens kunnen we uit de faculteitsstelling afleiden dat x=-1 een wortel is van de polynoom P(x), aangezien de numerieke waarde van P(x) bij x=-1 verdwijnt.
Omdat x=-1 dus een wortel is van de polynoom P(x), deelt u deze eenvoudigweg door x+1 om deze in factoren te ontbinden. En hiervoor gaan we de Ruffini-methode gebruiken:
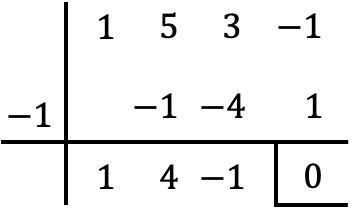
Het resultaat van de operatie is dus:
![]()
We kunnen de polynoom P(x) daarom als volgt ontbinden:
![]()
Oefening 3
Zoek met de faculteitsstelling of de polynoom P(x) deelbaar is door de binomiale Q(x) en, zo ja, vind ook een wortel van de polynoom P(x) en ontbind deze in factoren.
![]()
In dit geval is de polynoom die Q(x) deelt een binomiaal die alleen wordt gevormd door een x en een onafhankelijke term, dus we kunnen de factorstelling gebruiken.
En om te controleren of de polynoom P(x) deelbaar is door de polynoom Q(x), moeten we de numerieke waarde van de polynoom P(x) bepalen voor de onafhankelijke term van de polynoom Q(x) met veranderd teken, dat wil zeggen: dat wil zeggen bij x =-3:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
In dit geval is de numerieke waarde van de polynoom op x=-3 nul, dus P(x) is inderdaad deelbaar door Q(x).
Om deze reden leiden we uit de faculteitsstelling af dat x=-3 een wortel is van de polynoom P(x), aangezien P(-3) gelijk is aan nul.
Dus omdat x=-3 een wortel is van de polynoom P(x), moeten we deze delen door x+3 om deze in factoren te ontbinden. En hiervoor zullen we de regel van Ruffini gebruiken:
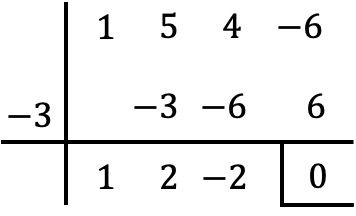
Het resultaat van de deling is dus:
![]()
En daarom kunnen we de polynoom P(x) op de volgende manier ontbinden:
![]()
Wat vind jij van de factorstelling? Denk je dat het nuttig is in de algebra? We lezen je in de reacties!
👀⬇⬇⬇👀