Unitaire matrix

Op deze pagina leggen we uit wat de unitaire matrix is en daarnaast illustreren we deze met verschillende oefeningen zodat deze goed begrepen wordt. Je ontdekt ook wat alle eigenschappen zijn van dit type matrix die zo belangrijk zijn voor lineaire algebra.

Wat is een unitaire matrix?

De definitie van unitaire matrix is als volgt:

Een unitaire matrix is een complexe matrix die, vermenigvuldigd met de geconjugeerde transpositiematrix, gelijk is aan de identiteitsmatrix. Dat wil zeggen dat aan de volgende voorwaarde is voldaan:

U\cdot U^* = U^* \cdot U =I

Goud

U

is een unitaire matrix en

U^*

zijn geconjugeerde transpositie.

Daarom impliceert deze voorwaarde dat de inverse van een eenheidsmatrix zijn geconjugeerde transpositie is , omdat, volgens de definitie van een inverse matrix, een matrix de inverse is van een andere als zijn product equivalent is aan de matrix d’identify .

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Daarom zal een unitaire matrix altijd een reguliere of niet-gedegenereerde matrix zijn, aangezien deze altijd een inverse zal hebben.

Aan de andere kant is de analoog van een unitaire matrix in een omgeving met reële getallen de orthogonale matrix , en in dit geval is het waar dat de unitaire matrix vermenigvuldigd met de transpositie gelijk is aan de identiteitsmatrix.

U\cdot U^t = U^t \cdot U =I

Dus in dit geval zou de inverse matrix van U direct de getransponeerde (of getransponeerde) matrix zijn.

Voorbeelden van eenheidsmatrices

Voorbeeld van een eenheidsmatrix met afmeting 2×2

Zodra we het concept van de eenheidsmatrix hebben gezien, zullen we een voorbeeld zien van een 2×2-eenheidsmatrix om het goed te begrijpen:

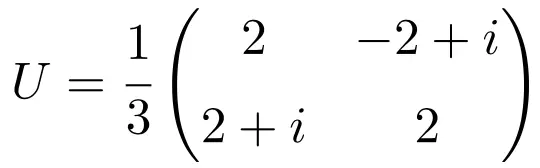
voorbeeld van een eenheidsmatrix met afmeting 2x2

Deze matrix is unitair omdat de vermenigvuldiging van zichzelf met zijn geconjugeerde matrix de identiteitsmatrix (of eenheidsmatrix) oplevert:

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

En zoals we eerder zagen, is elke unitaire matrix commuteerbaar met zijn geconjugeerde transpositie:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Eenheidsdiagonaalmatrixvoorbeeld

De diagonale matrix die alleen uit het complexe getal i bestaat, is ook een voorbeeld van een unitaire matrix, ongeacht de dimensie van de matrix. Hieronder heb je een opgeloste oefening die dit illustreert met een eenheidsmatrix van dimensie 3 × 3:

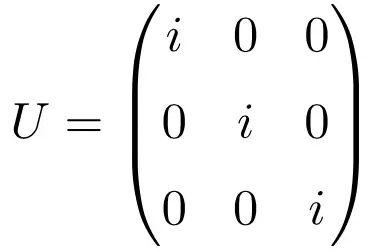
voorbeeld van een eenheidsmatrix met afmeting 3x3

Merk op dat als we het product van de matrix oplossen door zijn geconjugeerde transpositie, dit de identiteitsmatrix als oplossing oplevert:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

En hetzelfde gebeurt als we de matrices omgekeerd vermenigvuldigen:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

Het kenmerk van deze matrix is dat deze dient als voorbeeld van een unitaire matrix van welke dimensie dan ook, aangezien de matrix elke keer wordt gevormd door het denkbeeldige getal i op de hoofddiagonaal en de rest van de elementen nul zijn (0 ) het zal een unitaire matrix zijn.

Eigenschappen van een unitaire matrix

De eigenschappen van eenheidsmatrices zijn als volgt:

  • Het is duidelijk dat elke unitaire matrix een normale matrix is. Hoewel niet alle normale matrices unitaire matrices zijn.
  • Alle eenheidsmatrices zijn diagonaliseerbaar, dat wil zeggen dat ze kunnen worden omgezet in diagonale matrices.
  • De absolute waarde van de determinant van een eenheidsmatrix is altijd gelijk aan 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • voor iedereen

    n

    , de verzameling van alle eenheidsmatrices

    n\times n

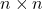
    met de matrixproductbewerking vormen ze een groep, de zogenaamde eenheidsgroep.

  • Zodat de vermenigvuldiging van twee eenheidsmatrices van dezelfde orde een andere eenheidsmatrix oplevert.
  • De modulus van alle eigenwaarden (of eigenwaarden) van een eenheidsmatrix is altijd gelijk aan 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • De eigenruimten van dit type matrix zijn orthogonaal.

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven