Op deze pagina ziet u wat een normale matrix is en voorbeelden van normale matrices. Daarnaast vind je stap voor stap de eigenschappen van dit soort matrices en oefeningen opgelost.
Wat is een normale matrix?
De normale arraydefinitie is:
Een normale matrix is een complexe matrix die, vermenigvuldigd met zijn geconjugeerde transpositiematrix, gelijk is aan het product van de geconjugeerde transpositie op zichzelf.
![]()
Goud
![]()
is de geconjugeerde getransponeerde matrix van
![]()
.
Als het echter reële getallenmatrices zijn, komt de voorgaande voorwaarde erop neer dat een matrix pendelt met zijn transpositie, dat wil zeggen:
![]()
Omdat de geconjugeerde transponeermatrix van een echte matrix uiteraard eenvoudigweg de transponeer- (of transponeer-) matrix is.
Voorbeelden van normale matrices
Voorbeeld met complexe getallen
De volgende complexe vierkante matrix met afmeting 2×2 is normaal:
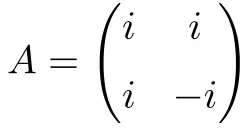
De demonstratie van de normaliteit ervan is hieronder bijgevoegd:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44b98cec879a8332c462d2393fbfbba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fddc406493ac1c81c86edf1ad6e58d0b_l3.png)
Voorbeeld met reële getallen
De volgende vierkante matrix met reële getallen van orde 2 is ook normaal:
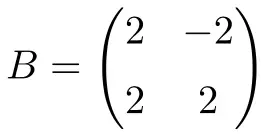
In dit geval, omdat het alleen reële getallen heeft, is het voldoende om te bewijzen dat het normaal is om te verifiëren dat de matrix commuteerbaar is met zijn transpositie:
![Rendered by QuickLaTeX.com \displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a320a8e300315c6a48bb8095266408ca_l3.png)
![Rendered by QuickLaTeX.com \displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6ad5bd62deeb5bcbf561a2ee6b29741_l3.png)
Eigenschappen van normale matrices
Normale matrices hebben de volgende kenmerken:
- Alle normale matrices zijn diagonaliseerbare matrices.
- Elke unitaire matrix is ook een normale matrix.
- Op dezelfde manier is een Hermitische matrix een normale matrix.
- Op dezelfde manier is een antihermitische matrix een normale matrix.
- Als A een normale matrix is, zijn de eigenwaarden (of eigenwaarden) van de geconjugeerde getransponeerde matrix A* de geconjugeerde eigenwaarden van A.
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91ee46b5f8dda0d51ecb57474f5b816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-48c80a017a9afd8b4cf3923757f4e945_l3.png)
- In normale matrices zijn de eigenvectoren (of eigenvectoren) die bij de verschillende eigenwaarden horen orthogonaal.
- Als een matrix alleen uit reële getallen bestaat en symmetrisch is, is het tegelijkertijd een normale matrix.
- Op dezelfde manier is een antisymmetrische reële matrix ook een normale matrix.
- Ten slotte is elke orthogonale matrix die uit reële getallen bestaat, ook een normale matrix.
Opgeloste oefeningen voor normale matrices
Oefening 1
Controleer of de volgende complexe matrix met afmeting 2 × 2 normaal is:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff27d19373c5a4dc8e95472ec295c657_l3.png)
Om aan te tonen dat de matrix normaal is, moeten we eerst de geconjugeerde transpositie berekenen:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17c96c654ce5b978f90a905b973d5ae7_l3.png)
En nu doen we de verificatie door matrix A te vermenigvuldigen met matrix A* in beide mogelijke richtingen:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36212e1d12cf35ea5dd27bd91d77ee56_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3db0fc8fdc948037452b4c6275896686_l3.png)
Het resultaat van beide vermenigvuldigingen is hetzelfde, dus matrix A is normaal.
Oefening 2
Laat zien dat de volgende reële matrix van maat 2 × 2 normaal is:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854e13859be417985691b5ed6d2a050f_l3.png)
Omdat we in dit geval te maken hebben met een omgeving met alleen reële getallen, volstaat het om te verifiëren dat het matrixproduct tussen de matrix A en zijn transpositie hetzelfde resultaat geeft, ongeacht de richting van de vermenigvuldiging:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1b6314188f394b3053d3dac0613cf5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2b33f892cd29c0ee232b88eaa4946cc_l3.png)
Het resultaat van beide producten is hetzelfde, dus matrix A is normaal.
Oefening 3
Bepaal of de volgende matrix van complexe getallen van orde 2 normaal is:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00075db37b045e08349f7d5b3f679570_l3.png)
Om te controleren of de matrix normaal is, moeten we eerst de geconjugeerde transpositie berekenen:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0b39733376eb2aef269012eb1d6c24be_l3.png)
En nu controleren we of de matrix A en zijn geconjugeerde transpositie schakelbaar zijn:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c207cb9842dacbaf9bc59d4aaff00473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bcf52f3da81fd7c56b090604c2b6f368_l3.png)
Het resultaat van beide vermenigvuldigingen is hetzelfde, dus matrix A is normaal.
Oefening 4
Controleer of de volgende reële matrix van dimensie 3×3 normaal is:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92ee07759c3e6e88af5a68479b5833ea_l3.png)
Omdat de matrix volledig uit reële elementen bestaat, volstaat het om te verifiëren dat het matrixproduct tussen de matrix A en zijn transpositie onafhankelijk is van de richting van de vermenigvuldiging:
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc7ee02c75239b430c7fc2418f43e343_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e661b877ee225983c797584e2b61d429_l3.png)
Het resultaat van beide producten is hetzelfde, dus matrix A is normaal.
Oefening 5
Bepaal of de volgende complexe matrix van orde 3×3 normaal is:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81ca0ac1da07c151a62dcfb06b4be877_l3.png)
Eerst berekenen we de geconjugeerde transpositie van de matrix:
![Rendered by QuickLaTeX.com \displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd0a2dfe1b8bfe18020ab68c1eb3bda6_l3.png)
Nu moeten we de matrixvermenigvuldigingen uitvoeren tussen matrix A en zijn geconjugeerde transpositie in beide mogelijke richtingen. De geconjugeerde transponeermatrix van A is echter gelijk aan de matrix A zelf, dus het is een Hermitische matrix. En daarom volgt uit de eigenschappen van normale matrices dat A een normale matrix is , omdat elke Hermitische matrix een normale matrix is.