Identiteit of matrixeenheid

Op deze pagina ziet u wat de identiteitsmatrix (of eenheidsmatrix) is en enkele voorbeelden. Verder leggen we uit wat de eigenschappen zijn van de identiteitsmatrix, hoe je met dit type matrix kunt werken en wat het resultaat is van de determinant ervan. Tenslotte vindt u de toepassingen die deze zeer specifieke matrix heeft.

Wat is de identiteitsmatrix?

De identiteitsmatrix (of eenheidsmatrix) is een vierkante matrix gevuld met nullen (0), behalve op de hoofddiagonaal, waar alle elementen enen zijn (1).

Dit is de definitie van de identiteitsmatrix of de eenheidsmatrix, maar je zult het zeker duidelijker zien aan de hand van voorbeelden:

Voorbeelden van identiteitsmatrices

Voorbeeld van identiteitsmatrix van dimensie 2 × 2

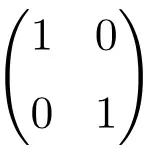
unieke identiteit of matrix van dimensie 2x2

Voorbeeld van een 3×3-bestelling Identiteitsmatrix

identiteit of unieke matrix van dimensie 3x3

Voorbeeld van een identiteitsmatrix van maat 4×4

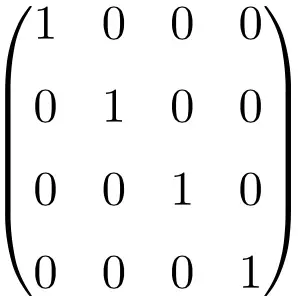
identiteit of unieke matrix van dimensie 4x4

Zoals je kunt zien, moeten we voor het construeren van de identiteitsmatrix nog steeds dezelfde procedure volgen: plaats de enen (1) op de hoofddiagonaal en de rest allemaal nullen (0). Het enige dat verandert, is de grootte van de tafel.

Eigenschappen van de identiteitstabel

De identiteitsmatrix, de eenheidsmatrix of zelfs de identieke matrix wordt veel gebruikt in de wiskunde, en dit komt door de kenmerken die dit type matrix bezit:

De identiteitsmatrix is een voorbeeld van een diagonaalmatrix .

Een unitaire matrix is zowel een bovenste als een onderste driehoekige matrix .

De identiteitsmatrix is eveneens een symmetrische matrix .

De plaatsvervanger van de identiteitsmatrix is zichzelf.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Het is een inverteerbare matrix. En wat het adjunct betreft, is de inverse van de eenheidsmatrix zelf:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Elke scalaire matrix kan worden verkregen door de vermenigvuldiging van een getal met de identiteitsmatrix:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Alle eigenwaarden (of eigenwaarden) van de Identieke matrix zijn 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Tenslotte is de identiteitsmatrix ook een voorbeeld van een permutatiematrix .

Bewerkingen met de identiteitsmatrix (of eenheidsmatrix).

Je denkt waarschijnlijk: dit is allemaal heel goed, maar… en waar is de Identiteitsmatrix voor? Was het maar een tafel met nullen en enen!

Hoewel je dit onderwerp misschien nog niet hebt gegeven, wordt identiteitsmatrix veel gebruikt in de wiskunde, sterker nog, dit type vierkante matrix is erg belangrijk in lineaire algebra. Het belangrijkste nut van de identiteitsmatrix is het gemak waarmee berekeningen van matrixbewerkingen mogelijk zijn. Laten we dus eens kijken hoe we met de Identiteitsmatrix kunnen werken:

Optellen en aftrekken met de identiteitsmatrix

Eén manier om getallen op de hoofddiagonaal van een matrix toe te voegen (of af te trekken) zonder de andere elementen te veranderen, is door de identiteitsmatrix te gebruiken, omdat deze slechts één eenheid aan die getallen toevoegt (of aftrekt). elementen:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Je kunt ook meer eenheden toevoegen aan of aftrekken van de elementen op de diagonaal door eerst de identiteitsmatrix te vermenigvuldigen met een scalair:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Vermenigvuldiging van een matrix met de identiteitsmatrix

Wanneer een matrix wordt vermenigvuldigd met de identiteitsmatrix, fungeert deze als een neutraal element , dat wil zeggen dat elke matrix vermenigvuldigd met de identiteitsmatrix resulteert in dezelfde matrix. Kijk eens naar het volgende voorbeeld:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Bovendien is de betekenis van het matrixproduct niet relevant, of met andere woorden, het maakt niet uit of we de identiteitsmatrix met rechts of met links vermenigvuldigen, omdat het resultaat altijd dezelfde matrix zal zijn. Om dit aan te tonen herhalen we de vorige oefening, maar deze keer vermenigvuldigen we de Identiteitsmatrix met de andere kant:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Kracht van de identiteitsmatrix

De kracht van de identiteitsmatrix resulteert altijd in de identiteitsmatrix, ongeacht de exponent waartoe we de matrix verheffen en de dimensie van de matrix.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Determinant van de identiteitsmatrix

Zoals je je al kunt voorstellen, is de determinant van de identiteitsmatrix (of eenheidsmatrix) altijd gelijk aan 1 , ongeacht de dimensie van de matrix.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Identiteitsmatrixtoepassingen

Tenslotte weet u na al deze informatie waarschijnlijk al hoe u de typische vraag moet beantwoorden: waarom is de identiteitsmatrix zo belangrijk? Relax, ik heb mezelf deze vraag ook al eerder gesteld. 😂

Zoals je zult hebben gemerkt, heeft de identiteitsmatrix veel toepassingen en daarom is hij zo interessant. Een van de toepassingen van de Eenhedenmatrix zijn bewerkingen, omdat het, zoals we hebben gezien, heel gemakkelijk is om er matrixbewerkingen mee uit te voeren.

Aan de andere kant wordt de identiteitsmatrix ook gebruikt om matrixvergelijkingen op te lossen. Om dit te doen gebruiken we de volgende inverse matrixeigenschap: het vermenigvuldigen van een matrix met zijn inverse matrix is gelijk aan de identiteitsmatrix. U kunt zien hoe u een vergelijking met matrices oplost door op de link te klikken.

Daarnaast wordt de identiteitsmatrix ook gebruikt om de inverse matrix te berekenen met de Gaussiaanse methode. Bij deze methode wordt een matrix naast de identiteitsmatrix geplaatst, waardoor een grotere matrix ontstaat. Vervolgens moet de oorspronkelijke matrix worden omgezet in een identiteitsmatrix door elementaire bewerkingen op de rijen toe te passen. Het lijkt erg ingewikkeld, maar in werkelijkheid is het niet zo veel. Er moet echter een hele procedure worden toegepast, dus als je meer geïnteresseerd bent, kun je zoeken hoe je een matrix kunt omkeren in de zoekmachine van de webpagina (van boven naar rechts).

Tenslotte is de Identiteitsmatrix ook bruikbaar voor het diagonaliseren van een matrix en het berekenen van de eigenwaarden (of eigenwaarden ervan). Omdat door middel van bepaalde bewerkingen, waarbij de eenheidsmatrix ingrijpt, de karakteristieke polynoom kan worden verkregen waaruit de eigenwaarden worden verkregen. Maar het is al een zeer geavanceerd onderwerp, daarom hebben we een hele super uitgebreide pagina gewijd aan matrixdiagonalisatie met voorbeelden en opgeloste oefeningen die dit uitleggen. Als u meer geïnteresseerd bent, kunt u deze gids opzoeken in onze zoekmachine (rechtsboven).