Bovenste en onderste driehoekige matrix

Op deze pagina zie je wat een driehoekige matrix is en de verschillende soorten driehoekige matrices, samen met voorbeelden. Daarnaast vind je hoe je de determinant van een driehoekige matrix berekent en wat de eigenschappen zijn van deze zeer interessante matrix. Ten slotte leggen we ook uit wat een Hessenberg-matrix is, aangezien het een matrix is die verband houdt met driehoekige matrices.

Wat is een driehoekige matrix?

Definitie van driehoekige matrix:

Een driehoekige matrix is een vierkante matrix waarin alle elementen boven of onder de hoofddiagonaal nul (0) zijn.

Driehoekige matrices worden veel gebruikt bij lineaire algebra-berekeningen, omdat het omkeren van een driehoekige matrix, het berekenen van de determinant ervan of zelfs het oplossen van stelsels van lineaire vergelijkingen met dit soort matrices veel eenvoudiger is dan met matrices die op alle posities andere elementen dan 0 hebben. .

bovenste driehoekige matrix

Een bovenste driehoekige matrix is een vierkante matrix waarvan de elementen onder de hoofddiagonaal nul (0) zijn.

Voorbeeld van een bovenste driehoekige matrix:

onderste driehoekige matrix

Een onderste driehoekige matrix is een vierkante matrix die een nul (0) heeft in elk element dat zich boven de hoofddiagonaal bevindt.

Voorbeeld van een onderste driehoekige matrix:

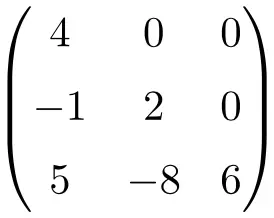
Soms worden deze matrices ook wel aangeduid met de letter U, voor de bovenste driehoekige matrix, en met de letter L, voor de onderste driehoekige matrix. Hoewel deze nomenclatuur voornamelijk in het Engels wordt gebruikt, staat de U in feite voor de bovenste driehoekige matrix en de L voor de onderste driehoekige matrix .

Voorbeelden van driehoekige matrices

2 × 2 dimensionale driehoekige matrix

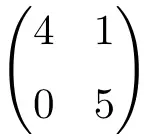
Voorbeeld van een bovenste driehoekige matrix van 2x2

Driehoekige matrix van orde 3×3

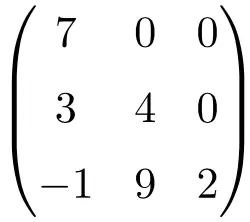
Voorbeeld van een 3x3 onderste driehoekige matrix

driehoekige matrix van maat 4×4

Voorbeeld van een bovenste driehoekige matrix van 4x4

Determinant van een driehoekige matrix

De determinant van een driehoekige matrix , zowel boven- als onderdriehoek, is het product van de elementen op de hoofddiagonaal.

Kijk eens naar de volgende oefening, waarin is opgelost hoe het voldoende is om de vermenigvuldiging van de elementen van de hoofddiagonaal van de driehoekige matrix te berekenen om de determinant ervan te vinden:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Deze stelling is gemakkelijk te demonstreren: bereken eenvoudigweg de determinant van een driehoekige matrix met blokken (of cofactoren). Deze demonstratie wordt hieronder gedetailleerd beschreven met behulp van een generieke driehoekige matrix:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Aan de andere kant weten we dat een matrix inverteerbaar is als de determinant ervan verschilt van 0. Dus als geen enkel element op de hoofddiagonaal 0 is, zal de driehoekige matrix ook inverteerbaar zijn en bijgevolg een regelmatige matrix zijn. Matrix.

Eigenschappen van de driehoekige matrix

Laten we nu eens kijken wat de eigenschappen van driehoekige matrices zijn:

Het product van twee bovenste driehoekige matrices is gelijk aan één bovenste driehoekige matrix. En omgekeerd: door twee lagere driehoekige matrices te vermenigvuldigen, ontstaat er nog een lagere driehoekige matrix.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

De transponering van een bovenste driehoekige matrix is een onderste driehoekige matrix, en omgekeerd: de transponering van een onderste driehoekige matrix is een bovenste driehoekige matrix.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Een driehoekige matrix is omkeerbaar als alle elementen op de hoofddiagonaal niet nul zijn, dat wil zeggen als ze verschillend zijn van nul. In zo’n geval is de inverse van een bovenste (onderste) driehoekige matrix ook een bovenste (onderste) driehoekige matrix.

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Bovendien zal de hoofddiagonaal van de omgekeerde matrix altijd de inverse van de elementen van de hoofddiagonaal van de oorspronkelijke driehoekige matrix bevatten.

Elke diagonale matrix is zowel een bovenste driehoekige matrix als een onderste driehoekige matrix, bijvoorbeeld:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Een scalaire matrix is dus ook een bovenste en onderste driehoekige matrix. Bijvoorbeeld de identiteitsmatrix:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Het is duidelijk dat de nulmatrix ook een bovenste en onderste driehoeksmatrix is, omdat de elementen boven en onder de hoofddiagonaal 0 zijn:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

De eigenwaarden (of eigenwaarden) van een driehoekige matrix zijn de elementen van de hoofddiagonaal.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Een bovenste of onderste driehoekige matrix is altijd in staat om te diagonaliseren op basis van eigenvectoren (of eigenvectoren).

Elke matrix kan worden ontbonden in het product van een onderste driehoekige matrix en een bovenste driehoekige matrix . Dat wil zeggen dat elke matrix kan worden omgezet in een driehoekige matrixvermenigvuldiging. Bovendien, als de matrix inverteerbaar is, is deze transformatie uniek. Om een matrix te ontbinden in factoren wordt vaak de LU-ontledingsmethode gebruikt.

Triangulariseer een matrix

Er zijn verschillende stellingen over matrices die kunnen worden driehoekig gemaakt door de basis te veranderen. Hier zullen we echter zien hoe we een matrix kunnen trianguleren door elementaire transformaties op de lijnen toe te passen, zoals bij de Gauss-methode.

Bijvoorbeeld:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

En op deze manier hebben we de oorspronkelijke matrix al driehoekig gemaakt.

Bedenk dat de elementaire transformaties die tussen lijnen in de Gauss-methode zijn toegestaan, de volgende zijn:

Vervang een lijn door de lineaire combinatie van andere lijnen.
Vermenigvuldig of deel alle termen in een rij met een ander getal dan 0.
Orderregels bewerken.

Hessenberg-matrix

De definitie van de Hessenberg-matrix is als volgt:

De Hessenberg-matrix is een “bijna” driehoekige matrix, dat wil zeggen dat al zijn elementen nul zijn, beginnend bij de eerste subdiagonaal (bovenste Hessenberg-matrix) of de eerste superdiagonaal (onderste Hessenberg-matrix).

Ik weet zeker dat het het beste wordt begrepen met een voorbeeld van een hogere Hessenberg-matrix en een ander voorbeeld van een lagere Hessenberg-matrix:

Matrix van Boven-Hessenberg

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Lagere Hessenberg-matrix

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Een matrix die zowel een bovenste als een onderste Hessenberg-matrix is, is een tridiagonale matrix .

Deze matrix is vernoemd naar Karl Hessenberg, een prominente Duitse ingenieur en wiskundige uit de 20e eeuw.

Ten slotte heeft dit type matrix de bijzonderheid dat als het wordt vermenigvuldigd met een driehoekige matrix, het resultaat altijd een Hessenberg-matrix is.