Stelling van Rouche-Frébenius

Op deze pagina zullen we ontdekken wat de stelling van Rouché Frobenius is en hoe je daarmee de rang van een matrix kunt berekenen. Je vindt er ook voorbeelden en oefeningen die stap voor stap worden opgelost met de stelling van Rouché-Frobenius.

Wat is de stelling van Rouché-Frobenius?

De stelling van Rouché-Frobenius is een methode voor het classificeren van stelsels van lineaire vergelijkingen. Met andere woorden, de stelling van Rouché-Frobenius wordt gebruikt om erachter te komen hoeveel oplossingen een stelsel vergelijkingen heeft zonder het op te lossen.

Er zijn 3 soorten stelsels vergelijkingen:

Systeemcompatibel bepaald (SCD): Het systeem heeft een unieke oplossing.
Onbepaald compatibel systeem (ICS): het systeem heeft oneindige oplossingen.
Systeem incompatibel (SI): Het systeem heeft geen oplossing.

Bovendien zal de stelling van Rouché-Frobenius ons later ook in staat stellen systemen op te lossen met behulp van de regel van Cramer .

Verklaring van de stelling van Rouché-Frobenius

De stelling van Rouché-Frobenius zegt dat

$\displaystyle \bm{A}$

is de matrix gevormd door de coëfficiënten van de onbekenden van een stelsel vergelijkingen. en de buik

$\displaystyle \bm{A'}$

, of uitgebreide matrix , is de matrix gevormd door de coëfficiënten van de onbekenden van een systeem van vergelijkingen en de onafhankelijke termen:

De stelling van Rouché-Frobenius stelt ons in staat te weten met welk type systeem van vergelijkingen we te maken hebben, afhankelijk van de rangorde van de matrices A en A’:

Als rang(A) = rang(A’) = aantal onbekenden ⟶ Bepaald compatibel systeem (SCD)
Als rang(A) = rang(A’) < aantal onbekenden ⟶ Onbepaald compatibel systeem (SCI)
als bereik (A)
$\bm{\neq}$

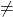
bereik (A’) ⟶ Incompatibel systeem (SI)

Zodra we weten wat de stelling van Rouché-Frobenius zegt, zullen we zien hoe we de stellingoefeningen van Rouché-Frobenius kunnen oplossen. Hier zijn 3 voorbeelden: een oefening die wordt opgelost met behulp van de stelling van elk type stelsel vergelijkingen.

Voorbeeld van een bepaald compatibel systeem (SCD)

$\begin{cases} 2x+y-3z=0 \\[1.5ex] x+2y-z= 1 \\[1.5ex] 4x-2y+z = 3\end{cases}$

De matrix A en de uitgebreide matrix A’ van het systeem zijn:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 1 & 2 & -1 & 1 \\[1.1ex] 4 & -2 & 1 & 3\end{array} \right)$

We berekenen nu de rangorde van de matrix A. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 1 & 2 & -1 \\[1.1ex] 4 & -2 & 1 \end{vmatrix} = 25 \neq 0$

Omdat de matrix een 3×3 determinant heeft die verschilt van 0, heeft matrix A rang 3:

$\displaystyle rg(A)=3$

Zodra we de rang van A kennen, berekenen we de rang van A’, die op zijn minst rang 3 zal zijn, omdat we zojuist hebben gezien dat deze een determinant van orde 3 heeft die verschilt van 0. Bovendien kan deze niet van rang 4 zijn, aangezien we geen enkele determinant van orde 4 kunnen maken. Daarom is de matrix A’ ook van rang 3:

$\displaystyle rg(A')=3$

Omdat de rangorde van matrix A dus gelijk is aan de rangorde van matrix A’ en aan het aantal onbekenden van het systeem (3), weten we door de stelling van Rouché Frobenius dat het een Compatibel Bepaald Systeem (SCD) is. :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Voorbeeld van een onbepaald compatibel systeem (ICS)

$\begin{cases} x-y+2z=1 \\[1.5ex] 3x+2y+z= 5 \\[1.5ex] 2x+3y-z = 4\end{cases}$

De matrix A en de uitgebreide matrix A’ van het systeem zijn:

$\displaystyle A= \left( \begin{array}{ccc} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & -1 & 2 & 1 \\[1.1ex] 3 & 2 & 1 & 5 \\[1.1ex] 2 & 3 & -1 & 4 \end{array} \right)$

We berekenen nu de rangorde van de matrix A. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & -1 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 2 & 3 & -1 \end{vmatrix} = 0$

De determinant van de gehele matrix A geeft 0 en is dus niet van rang 3. Om te zien of deze van rang 2 is, moeten we een submatrix in A vinden waarvan de determinant verschilt van 0. Bijvoorbeeld die uit de linkerbovenhoek :

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Omdat de matrix een 2×2 determinant heeft die verschilt van 0, heeft matrix A rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus proberen we de andere mogelijke 3×3 determinanten:

$\displaystyle \begin{vmatrix}1 & -1 & 1 \\[1.1ex] 3 & 2 & 5 \\[1.1ex] 2 & 3 & 4\end{vmatrix} = 0 \quad \begin{vmatrix}1 & 2 & 1 \\[1.1ex] 3 & 1 & 5 \\[1.1ex] 2 & -1 & 4\end{vmatrix} = 0 \quad \begin{vmatrix} -1 & 2 & 1 \\[1.1ex] 2 & 1 & 5 \\[1.1ex] 3 & -1 & 4\end{vmatrix} = 0$

Alle 3×3 determinanten van matrix A’ zijn 0, dus matrix A’ zal ook niet van rang 3 zijn. Binnenin heeft het echter determinanten van orde 2 die verschillen van 0. Bijvoorbeeld:

$\displaystyle \begin{vmatrix} 1 & -1 \\[1.1ex] 3 & 2 \end{vmatrix} = 5 \neq 0$

Dus de matrix A’ zal van rang 2 zijn :

$\displaystyle rg(A')=2$

De omvang van matrix A is gelijk aan de omvang van matrix A’, maar deze zijn kleiner dan het aantal onbekenden van het systeem (3). Daarom is het volgens de stelling van Rouché-Frobenius een onbepaald compatibel systeem (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Voorbeeld van incompatibel systeem (IS)

$\begin{cases} 2x+y-2z=3 \\[1.5ex] 3x-2y+z= 2 \\[1.5ex] x+4-5z = 3 \end{cases}$

De matrix A en de uitgebreide matrix A’ van het systeem zijn:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -2 & 3 \\[1.1ex] 3 & -2 & 1 & 2 \\[1.1ex] 1 & 4 & -5 & 3 \end{array} \right)$

We berekenen nu de rangorde van de matrix A. Om dit te doen, controleren we of de determinant van de gehele matrix anders is dan 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -2 \\[1.1ex] 3 & -2 & 1 \\[1.1ex] 1 & 4 & -5 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & -2 \end{vmatrix} = -7 \neq 0$

Omdat de matrix een determinant van orde 2 heeft die verschilt van 0, heeft matrix A rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus nu proberen we bijvoorbeeld met de determinant van de laatste 3 kolommen:

$\displaystyle \begin{vmatrix} 1 & -2 & 3 \\[1.1ex] -2 & 1 & 2 \\[1.1ex] 4 & -5 & 3 \end{vmatrix} = 3 \neq 0$

Aan de andere kant bevat matrix A’ wel een determinant waarvan het resultaat anders is dan 0, daarom zal matrix A’ rang 3 hebben :

$\displaystyle rg(A')=3$

Omdat de rangorde van matrix A kleiner is dan de rangorde van matrix A’, leiden we daarom uit de stelling van Rouché-Frobenius af dat het een incompatibel systeem (SI) is :

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}$

Problemen van de stelling van Rouché-Frobenius opgelost

Oefening 1

Bepaal het type van het volgende stelsel vergelijkingen met 3 onbekenden met behulp van de stelling van Rouché-Frobenius:

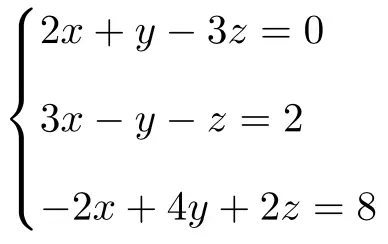
Opgeloste oefening van de stelling van Rouche - frobenius

zie oplossing

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & -3 & 0 \\[1.1ex] 3 & -1 & -1 & 2 \\[1.1ex] -2 & 4 & 2 & 8 \end{array} \right)$

We moeten nu de rangorde van de matrix A vinden. Om dit te doen, controleren we of de determinant van de matrix anders is dan 0:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & -3 \\[1.1ex] 3 & -1 & -1 \\[1.1ex] -2 & 4 & 2 \end{vmatrix} = -4+2-36+6+8-6=-30 \bm{\neq 0}$

De matrix heeft een derde orde determinant die verschilt van 0, de matrix A heeft rang 3:

$\displaystyle rg(A)=3$

Zodra we de rang van A kennen, berekenen we de rang van A’. Dit zal op zijn minst van rang 3 zijn, omdat we zojuist hebben gezien dat er een determinant in zit van orde 3 die verschilt van 0. Bovendien kan het niet van rang 4 zijn, omdat we geen 4×4-determinant kunnen maken. Daarom is de matrix A’ ook van rang 3:

$\displaystyle rg(A')=3$

Dankzij de stelling van Rouché-Frobenius weten we dus dat het een bepaald compatibel systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.

Oefening 2

Classificeer het volgende stelsel vergelijkingen met 3 onbekenden met behulp van de stelling van Rouché-Frobenius:

zie oplossing

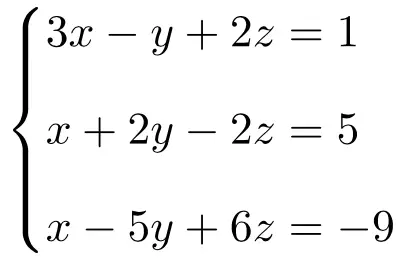
We construeren eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc}3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -1 & 2 & 1 \\[1.1ex] 1 & 2 & -2 & 5 \\[1.1ex] 1 & -5 & 6 & -9 \end{array} \right)$

Laten we nu het bereik van matrix A berekenen:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -1 & 2 \\[1.1ex] 1 & 2 & -2 \\[1.1ex] 1 & -5 & 6 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 3 & -1 \\[1.1ex] 1 & 2 \end{vmatrix} = 7 \neq 0$

Matrix A heeft dus rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus proberen we de andere mogelijke 3×3 determinanten:

$\displaystyle \begin{vmatrix}-1 & 2 & 1 \\[1.1ex] 2 & -2 & 5 \\[1.1ex] -5 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix}3 & 2 & 1 \\[1.1ex] 1 & -2 & 5 \\[1.1ex] 1 & 6 & -9\end{vmatrix} = 0 \quad \begin{vmatrix} 3 & -1 & 1 \\[1.1ex] 1 & 2 & 5 \\[1.1ex] 1 & -5 & -9\end{vmatrix} = 0$

Alle 3×3 determinanten van matrix A’ zijn 0, dus matrix A’ zal ook niet van rang 3 zijn. Binnenin heeft het echter veel determinanten van orde 2 die verschillen van 0. Bijvoorbeeld:

$\displaystyle \begin{vmatrix} -1 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -2 \neq 0$

Dus de matrix A’ zal van rang 2 zijn :

$\displaystyle rg(A')=2$

De rangorde van matrix A is gelijk aan de rangorde van matrix A’, maar deze twee zijn kleiner dan het aantal onbekenden van het systeem (3). Daarom weten we door de stelling van Rouché-Frobenius dat het een onbepaald compatibel systeem (ICS) is:

Oefening 3

Bepaal welk type systeem het volgende stelsel vergelijkingen gebruikt volgens de stelling van Rouché-Frobenius:

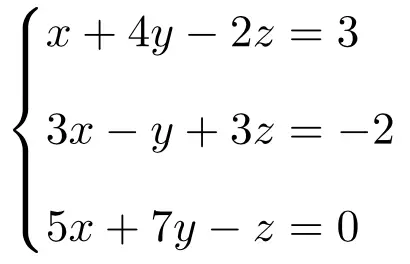
oefening stap voor stap opgelost van de rouche-stelling - frobenius

zie oplossing

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 4 & -2 & 3 \\[1.1ex] 3 & -1 & 3 & -2 \\[1.1ex] 5 & 7 & -1 & 0 \end{array} \right)$

Laten we nu het bereik van matrix A berekenen:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 4 & -2 \\[1.1ex] 3 & -1 & 3 \\[1.1ex] 5 & 7 & -1\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 1 & 4 \\[1.1ex] 3 & -1 \end{vmatrix} = -13 \neq 0$

Matrix A heeft dus rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, maar niet de determinant van de laatste 3 kolommen:

$\displaystyle \begin{vmatrix} 4 & -2 & 3 \\[1.1ex]-1 & 3 & -2 \\[1.1ex] 7 & -1 & 0 \end{vmatrix} = -40 \neq 0$

Daarom heeft de matrix A’ rang 3 :

$\displaystyle rg(A')=3$

De rangorde van matrix A is kleiner dan de rangorde van matrix A’, we kunnen daarom uit de stelling van Rouché-Frobenius afleiden dat het een incompatibel systeem (SI) is :

Oefening 4

Bepaal het type van het volgende stelsel vergelijkingen met 3 onbekenden met behulp van de stelling van Rouché-Frobenius:

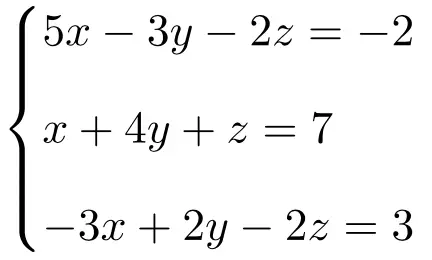
Rouche - Stelling van Frobenius opgeloste oefening met 3 onbekenden en 3 vergelijkingen

zie oplossing

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 5 & -3 & -2 & -2 \\[1.1ex] 1 & 4 & 1 & 7 \\[1.1ex]-3 & 2 & -2 & 3 \end{array} \right)$

We moeten nu de rangorde van de matrix A berekenen. Om dit te doen, lossen we de determinant van de matrix op met de Sarrus-regel:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 5 & -3 & -2 \\[1.1ex] 1 & 4 & 1 \\[1.1ex]-3 & 2 & -2 \end{vmatrix} = -40+9-4-24-10-6=-75 \bm{\neq 0}$

De matrix heeft een derde orde determinant die verschilt van 0, de matrix A heeft rang 3:

$\displaystyle rg(A)=3$

Daarom heeft de matrix A’ ook rang 3 , aangezien deze altijd minimaal rang A heeft en niet rang 4 kan zijn omdat we geen enkele 4×4 determinant kunnen oplossen.

$\displaystyle rg(A')=3$

Dankzij de toepassing van de stelling van Rouché-Frobenius weten we dus dat het systeem een Compatible Bepaald Systeem (SCD) is, omdat het bereik van A gelijk is aan het bereik van A’ en het aantal onbekenden.

Oefening 5

Bepaal welk type systeem het volgende stelsel vergelijkingen de stelling van Rouché-Frobenius gebruikt:

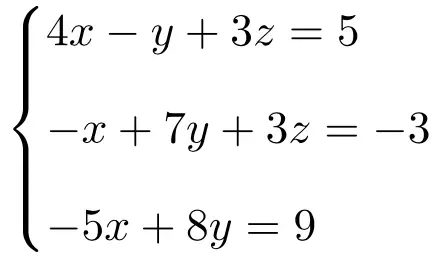
voorbeeld van de stelling van Rouche - frobenius

zie oplossing

We maken eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 3 & 5 \\[1.1ex] -1 & 7 & 3 & -3 \\[1.1ex] -5 & 8 & 0 & 9 \end{array} \right)$

Laten we nu het bereik van matrix A berekenen:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 3 \\[1.1ex] -1 & 7 & 3 \\[1.1ex] -5 & 8 & 0\end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 4 & -1 \\[1.1ex] -1 & 7 \end{vmatrix} = 27 \neq 0$

Matrix A is daarom van rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. De determinant van de eerste 3 kolommen die we al kennen geeft 0, maar de determinant van de laatste 3 kolommen geeft niet:

$\displaystyle \begin{vmatrix} -1 & 3 & 5 \\[1.1ex] 7 & 3 & -3 \\[1.1ex] 8 & 0 & 9\end{vmatrix} = -408 \neq 0$

Daarom heeft de matrix A’ rang 3 :

$\displaystyle rg(A')=3$

En ten slotte passen we het domein toe op de stelling van Rouché-Frobenius: het domein van de matrix A is kleiner dan het domein van de matrix A’, het is daarom een incompatibel systeem (SI) :

Oefening 6

Classificeer het volgende systeem van vergelijkingen van orde 3 met de stelling van Rouché-Frobenius:

$\begin{cases} 6x-2y+4z=1 \\[1.5ex] -2x+4y+3z= 7 \\[1.5ex] 8x-6y+z = -6\end{cases}$

zie oplossing

We construeren eerst de matrix A en de uitgebreide matrix A’ van het systeem:

$\displaystyle A= \left( \begin{array}{ccc} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 6 & -2 & 4 & 1 \\[1.1ex] -2 & 4 & 3 & 7 \\[1.1ex] 8 & -6 & 1 & -6 \end{array} \right)$

Laten we nu het bereik van matrix A berekenen:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 6 & -2 & 4 \\[1.1ex] -2 & 4 & 3 \\[1.1ex] 8 & -6 & 1 \end{vmatrix} = 0$

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Matrix A heeft dus rang 2:

$\displaystyle rg(A)=2$

Zodra we de rang van A kennen, berekenen we de rang van A’. We weten al dat de determinant van de eerste 3 kolommen 0 oplevert, dus proberen we de andere mogelijke 3×3 determinanten:

$\displaystyle \begin{vmatrix} -2 & 4 & 1 \\[1.1ex]4 & 3 & 7 \\[1.1ex] -6 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix}6 & 4 & 1 \\[1.1ex] -2 & 3 & 7 \\[1.1ex] 8 & 1 & -6\end{vmatrix} = 0 \quad \begin{vmatrix} 6 & -2 & 1 \\[1.1ex] -2 & 4 & 7 \\[1.1ex] 8 & -6 & -6\end{vmatrix} = 0$

Alle 3×3 determinanten van matrix A’ zijn 0, dus matrix A’ zal ook niet van rang 3 zijn. Binnenin heeft het echter determinanten van orde 2 die verschillen van 0. Bijvoorbeeld:

$\displaystyle \begin{vmatrix} 6 & -2 \\[1.1ex] -2 & 4 \end{vmatrix} = 20 \neq 0$

Dus de matrix A’ zal van rang 2 zijn :

$\displaystyle rg(A')=2$

Ten slotte weten we door toepassing van de stelling van Rouché-Frobenius dat het een onbepaald compatibel systeem (ICS) is, omdat het bereik van matrix A gelijk is aan het bereik van matrix A’, maar deze twee zijn kleiner dan het aantal onbekenden in de systeem(3):

Stelling van rouche-frébenius

Wat is de stelling van Rouché-Frobenius?

Verklaring van de stelling van Rouché-Frobenius

Voorbeeld van een bepaald compatibel systeem (SCD)

Voorbeeld van een onbepaald compatibel systeem (ICS)

Voorbeeld van incompatibel systeem (IS)

Problemen van de stelling van Rouché-Frobenius opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Laat een reactie achter Reactie annuleren