Eigenschappen van determinanten

In deze sectie zullen we zien wat alle eigenschappen van determinanten zijn. Bovendien demonstreren we elke woning met een voorbeeld, zodat u ze volledig begrijpt. En daarnaast vind je oefeningen gerelateerd aan de eigenschappen van dedeterminanten.

Hieronder lichten we elke eigenschap van de determinanten één voor één toe, maar als u dat liever heeft, kunt u direct naar de onderstaande overzichtstabel gaan. 😉

Eigenschap 1: Determinant van de getransponeerde matrix

De determinant van een matrix is gelijkwaardig aan de determinant van de getransponeerde matrix.

$\lvert A \rvert = \lvert A^t \rvert$

Voorbeeld:

$\lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}$

Nu transponeren we de 2×2-matrix en lossen we de determinant op. Merk op dat we hetzelfde resultaat verkrijgen als voorheen:

$\lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}$

Eigenschap 2: Determinant met een rij of kolom gevuld met nullen

Als een determinant een rij of kolom heeft gevuld met nullen, retourneert de determinant 0.

$\displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0$

Voorbeeld:

$\begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}$

In beide voorbeelden komen de determinanten uit op 0. Omdat de tweede rij van de eerste determinant geheel uit nullen bestaat en de derde kolom van de tweede determinant ook uit allemaal nullen bestaat.

Property 3: Determinant met twee gelijke rijen of kolommen

Als een determinant twee gelijke of meerdere rijen of twee kolommen heeft, is de determinant nul (0).

Als er dus een lineaire combinatie is tussen rijen of kolommen, dat wil zeggen dat ze lineair afhankelijk zijn, geeft de determinant 0.

Voorbeeld:

$\begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0$

In dit geval geeft de determinant 0 omdat de kolommen 2 en 3 gelijk zijn.

Eigenschap 4: Wijzig de rijen of kolommen van een determinant

Als twee rijen of twee kolommen ten opzichte van elkaar worden gewijzigd, geeft de determinant hetzelfde resultaat, maar met een ander teken.

$\displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}$

Voorbeeld:

$\begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}$

Nu veranderen we de volgorde van kolommen 2 en 3 ten opzichte van elkaar. Merk op dat het resultaat hetzelfde is, maar met een ander teken:

$\begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}$

Property 5: Vermenigvuldig een rij van een determinant met een scalair

Het vermenigvuldigen van alle elementen in een hele rij of kolom met een reëel getal is hetzelfde als het vermenigvuldigen van het resultaat van de determinant met dat getal.

$\displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

$\displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}$

Voorbeeld:

$\displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}$

Nu nemen we dezelfde determinant en vermenigvuldigen we een hele lijn met 2. Je zult zien dat het resultaat dat van de vorige determinant zal zijn, maar dan vermenigvuldigd met 2, of 10:

$\displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}$

Eigenschap 6: Determinant van het matrixproduct

De determinant van het product van twee matrices is gelijk aan het product van de determinant van elke matrix afzonderlijk.

$\displaystyle \lvert A \cdot B \rvert = \lvert A \rvert \cdot \lvert B \rvert$

Voorbeeld:

Om deze eigenschap van determinanten aan te tonen, zullen we de determinant van de vermenigvuldiging van de volgende twee matrices op twee mogelijke manieren berekenen:

$\displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}$

We zullen eerst de twee matrices vermenigvuldigen en vervolgens de determinant van de resulterende matrix berekenen:

$\displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}$

Nu berekenen we de determinant van elke matrix afzonderlijk en vermenigvuldigen we vervolgens de resultaten:

$\displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}$

Zoals je kunt zien, geeft het eerst uitvoeren van het matrixproduct en daarna de determinant hetzelfde resultaat als het eerst uitvoeren van de determinant van elke matrix en vervolgens het vermenigvuldigen van de resultaten.

Aan de andere kant is deze voorwaarde niet van toepassing op optel- en aftrekkingsoperaties, dat wil zeggen dat de determinant van het optellen (of aftrekken) van twee matrices niet hetzelfde resultaat geeft als het optellen (of aftrekken) van de determinanten van twee matrices afzonderlijk.

Eigenschap 7: Determinant van de inverse matrix

Als een matrix inverteerbaar is, komt de determinant van zijn inverse overeen met de inverse van de determinant van de oorspronkelijke matrix.

$\displaystyle \begin{vmatrix} A^{-1} \end{vmatrix} = \cfrac{1}{\lvert A \rvert}$

Voorbeeld:

We zullen deze eigenschap verifiëren door eerst de inverse van een matrix te berekenen en vervolgens de determinant ervan op te lossen. We zullen zien dat het resultaat gelijk is aan het vinden van de determinant van de oorspronkelijke matrix en het omkeren ervan.

We keren daarom de volgende matrix om en berekenen de determinant ervan:

$\displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}$

$\displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}$

$\displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}$

En nu lossen we de determinant van de oorspronkelijke matrix op en doen we het omgekeerde:

$\displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2$

$\displaystyle \begin{vmatrix}A^{-1}\end{vmatrix}= \cfrac{\bm{1}}{\bm{2}}$

Zoals u kunt zien, zijn de resultaten van beide bewerkingen identiek. De eigenschap is dus bewezen.

Property 8: Vervang de lijn van een bepaler

De rij van een determinant kan worden vervangen door dezelfde rij op te tellen (of af te trekken) plus (of min) een andere rij vermenigvuldigd met een getal.

Voorbeeld:

Met het volgende voorbeeld zullen we deze eigenschap controleren. We berekenen eerst een determinant, daarna gaan we aan de slag met een rij van de determinant en herberekenen we het resultaat ervan. U zult zien hoe we in beide gevallen hetzelfde resultaat verkrijgen.

Laten we dus eerst een 3×3 determinant berekenen met de regel van Sarrus:

$\begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}$

Nu voegen we in regel 2 de eerste regel vermenigvuldigd met 2 toe:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}$

En we lossen de determinant op na het transformeren van een van zijn lijnen:

$\displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}$

In beide gevallen was het resultaat -3. Er wordt dus aangetoond dat het resultaat van een determinant niet verandert als een rij wordt vervangen door de som van dezelfde rij plus een andere rij vermenigvuldigd met een getal.

Property 9: Determinant van een driehoekige matrix

De determinant van een driehoekige matrix is het product van de elementen van de hoofddiagonaal.

Voorbeeld:

We zullen als voorbeeld de determinant van de volgende driehoekige matrix oplossen:

$\begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}$

Property 10: Determinant van een diagonale matrix

De determinant van een diagonale matrix is gelijk aan de vermenigvuldiging van de elementen van de hoofddiagonaal.

Voorbeeld:

Laten we als voorbeeld de determinant van de volgende diagonale matrix nemen:

$\begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}$

Samenvattende tabel met eigenschappen van determinanten

De eigenschappen van de toegelichte determinanten kunnen worden samengevat in de volgende tabel:

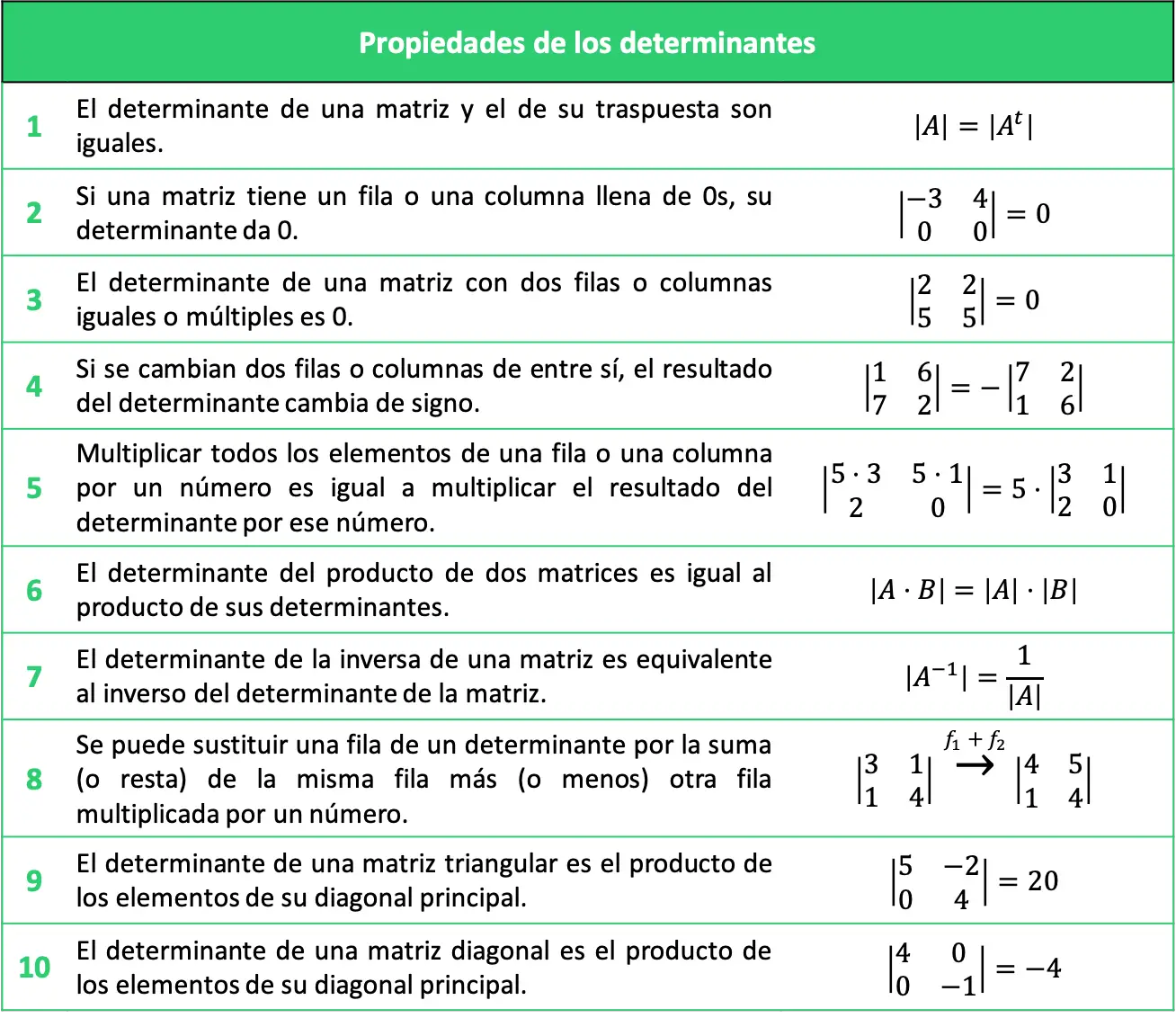
Opgeloste oefeningen met de eigenschappen van determinanten

Oefening 1

Los de volgende determinant op:

$\displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}$

zie oplossing

Als een determinant een rij of kolom gevuld met nullen heeft, retourneert de determinant 0 (eigenschap 2). Het resultaat van de determinant is dus 0, omdat de derde kolom gevuld is met nullen.

Oefening 2

Los de volgende determinant op:

$\displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}$

zie oplossing

Als een determinant twee gelijke of meerdere rijen of twee kolommen heeft, retourneert de determinant 0 (eigenschap 3). Daarom is het resultaat van de determinant 0, omdat de eerste rij en de derde rij gelijk zijn.

Oefening 3

Bereken de volgende determinant:

$\displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}$

zie oplossing

Als een determinant twee gelijke of meerdere rijen of twee kolommen heeft, retourneert de determinant 0 (eigenschap 3). Daarom is het resultaat van de determinant 0, omdat de vierde kolom het dubbele is van de eerste kolom.

Oefening 4

We kennen het resultaat van een determinant, hoewel we de elementen van de matrix niet kennen:

$\displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3$

Bereken uit het resultaat van de vorige determinant en de eigenschappen van de determinanten het resultaat van de volgende determinanten:

$\displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}$

zie oplossing

Voor)

$\begin{pmatrix} a & c \\ b & d \end{pmatrix}$

is de getransponeerde matrix van

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$

. En de determinant van een matrix is gelijk aan de determinant van zijn getransponeerde matrix (eigenschap 1). Daarom is het resultaat van deze determinant ook 3.

$\displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}$

b) In de bepaling

$\begin{vmatrix} b & a \\ d & c \end{vmatrix}$

kolommen 1 en 2 zijn aangepast met betrekking tot de bepaler van de verklaring

$\begin{vmatrix} a & b \\ c & d \end{vmatrix}$

. Daarom is het resultaat volgens eigenschap 4 hetzelfde als het resultaat van de bepaler van de uitspraak, maar met een ander teken, namelijk -3.

$\displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}$

c) In de bepaling

$\begin{vmatrix} a & 3b \\ c & 3d \end{vmatrix}$

de gehele tweede kolom van de determinant van de uitspraak is vermenigvuldigd met 3. Daarom kunnen we uit eigenschap 5 afleiden dat het resultaat ervan ook het resultaat zal zijn van de determinant van de uitspraak vermenigvuldigd met 3, dat wil zeggen 9.

$\displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}$

Oefening 5

We kennen het resultaat van deze twee determinanten:

$\displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8$

$\displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4$

Bereken op basis van deze informatie:

$\displaystyle \vert A \cdot B \vert$

zie oplossing

Om het resultaat van de determinant te berekenen, is het niet nodig om 4×4 matrices te vermenigvuldigen. Omdat de determinant van het product van twee matrices gelijk is aan het product van de determinant van elke matrix afzonderlijk (eigenschap 6). Nog:

$\vert A \cdot B \vert = \vert A \vert \cdot \vert B \vert = 8 \cdot (-4) = \bm{-32}$

Eigenschap 1: Determinant van de getransponeerde matrix

Voorbeeld:

Eigenschap 2: Determinant met een rij of kolom gevuld met nullen

Voorbeeld:

Property 3: Determinant met twee gelijke rijen of kolommen

Voorbeeld:

Eigenschap 4: Wijzig de rijen of kolommen van een determinant

Voorbeeld:

Property 5: Vermenigvuldig een rij van een determinant met een scalair

Voorbeeld:

Eigenschap 6: Determinant van het matrixproduct

Voorbeeld:

Eigenschap 7: Determinant van de inverse matrix

Voorbeeld:

Property 8: Vervang de lijn van een bepaler

Voorbeeld:

Property 9: Determinant van een driehoekige matrix

Voorbeeld:

Property 10: Determinant van een diagonale matrix

Voorbeeld:

Samenvattende tabel met eigenschappen van determinanten

Opgeloste oefeningen met de eigenschappen van determinanten

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren