Bereken de determinant van een 3x3-matrix met de regel van Sarrus

Op deze pagina leer je wat de determinant van een 3×3 vierkante matrix is. Je zult zien hoe je de determinanten van orde 3 kunt oplossen met behulp van de Sarrus-regel. En daarnaast heb je stap voor stap opgeloste voorbeelden en oefeningen, zodat je het perfect kunt oefenen en begrijpen.

Wat is de determinant van een 3×3-matrix?

Een determinant van orde 3 is een matrix met dimensie 3×3 , weergegeven door een verticale balk aan elke kant van de matrix. Als we bijvoorbeeld de volgende matrix hebben:

$\displaystyle A = \begin{pmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{pmatrix}$

De determinant van matrix A wordt als volgt weergegeven:

$\displaystyle \lvert A \rvert = \begin{vmatrix} 2 & 0 & 4 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 1 & 6 & -2 \end{vmatrix}$

Zoals je hebt gezien, is het schrijven van de determinant van een vierkante matrix van orde 3 eenvoudig. Laten we nu kijken hoe we het kunnen oplossen:

Hoe bereken je een determinant van orde 3?

Om de determinanten van 3×3 matrices te maken, moet je de regel van Sarrus toepassen:

Sarrus-regel

De regel van Sarrus zegt dat om een determinant van orde 3 te berekenen, we het product van de elementen van de grote diagonaal en het product van de evenwijdige diagonalen met hun corresponderende tegengestelde hoekpunten moeten optellen, en vervolgens het product van de elementen van de kleine diagonaal moeten aftrekken en het product van hun evenwijdige diagonalen met hun overeenkomstige tegengestelde hoekpunten.

Op deze manier geschreven kan het een beetje moeilijk te begrijpen zijn, maar kijk eens hoe de berekening van 3×3 determinanten wordt gedaan met het volgende diagram en voorbeelden:

Voorbeelden van 3×3 determinanten:

$\begin{aligned} \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] -1 & 1 & 0 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} & = 2 \cdot 1 \cdot 1 + 1 \cdot 0 \cdot (-2) + (-1) \cdot 4 \cdot 3 - (-2) \cdot 1 \cdot 3 - 4 \cdot 0 \cdot 2- (-1) \cdot 1 \cdot 1 \\ & = 2 + 0 -12 +6 - 0 +1 \\[2ex] & = \bm{-3} \end{aligned}$

$\begin{aligned} \begin{vmatrix} 1 & 0 & 2 \\[1.1ex] 3 & 2 & 1 \\[1.1ex] 4 & -3 & -1 \end{vmatrix} & = 1\cdot 2 \cdot (-1) + 0 \cdot 1 \cdot 4 +3 \cdot (-3) \cdot 2 - 4 \cdot 2 \cdot 2 - (-3) \cdot 1 \cdot 1- 3 \cdot 0 \cdot (-1) \\ & = -2 +0 -18 - 16 +3- 0 \\[2ex] & = \bm{-33} \end{aligned}$

Opgeloste problemen van determinanten van 3 × 3 matrices

Oefening 1

Los de volgende 3×3 determinant op:

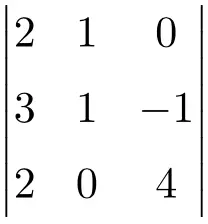
Concreet voorbeeld van de determinant van een 3x3-matrix

zie oplossing

Om de determinant van een 3×3 matrix op te lossen moeten we de regel van Sarrus toepassen:

$\displaystyle\begin{aligned} \begin{vmatrix} 2 & 1 & 0 \\[1.1ex] 3 & 1 & -1 \\[1.1ex] 2 & 0 & 4 \end{vmatrix} & = 2 \cdot 1 \cdot 4 + 1 \cdot (-1) \cdot 2 + 3 \cdot 0 \cdot 0 - 2 \cdot 1 \cdot 0 - 0 \cdot (-1) \cdot 2- 3 \cdot 1 \cdot 4 \\ & = 8 -2 +0 -0- 0-12 \\[2ex] & = \bm{-6} \end{aligned}$

Oefening 2

Bereken de volgende determinant van orde 3:

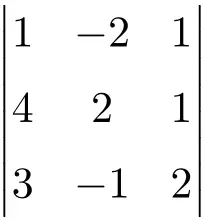
oefening stap voor stap opgelost van de determinant van een 3x3 matrix

zie oplossing

Om de determinant van een matrix van de derde orde te berekenen, moeten we de regel van Sarrus gebruiken:

$\displaystyle\begin{aligned} \begin{vmatrix} 1 & -2 & 1 \\[1.1ex] 4 & 2 & 1 \\[1.1ex] 3 & -1 & 2 \end{vmatrix} & = 1 \cdot 2 \cdot 2 + (-2) \cdot 1 \cdot 3 + 4 \cdot (-1) \cdot 1 - 3 \cdot 2 \cdot 1 - (-1) \cdot 1 \cdot 1 - 4 \cdot (-2) \cdot 2 \\ & = 4 -6 -4 -6+1+16 \\[2ex] & = \bm{5} \end{aligned}$

Oefening 3

Zoek de oplossing voor de determinant van de volgende 3×3-matrix:

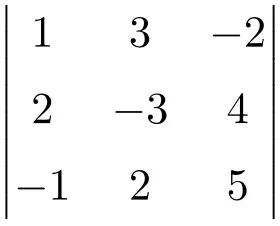
oefeningen stap voor stap opgelost voor determinanten van 3x3 matrices

zie oplossing

Om een determinant van een 3×3-matrix te maken, moeten we de regel van Sarrus gebruiken:

$\displaystyle\begin{aligned} \begin{vmatrix}1 & 3 & -2 \\[1.1ex] 2 & -3 & 4 \\[1.1ex] -1 & 2 & 5 \end{vmatrix} & = \\ & = 1 \cdot (-3) \cdot 5 + 3 \cdot 4 \cdot (-1) + 2 \cdot 2 \cdot (-2) \ - \\[1.1ex] & \phantom{=} - (-1) \cdot (-3) \cdot (-2) - 2 \cdot 4 \cdot 1 - 2 \cdot 3 \cdot 5 \\[2.5ex] & = -15 -12 -8 +6-8-30 \\[2.5ex] & = \bm{-67} \end{aligned}$

Oefening 4

Vind de oplossing voor de determinant van de volgende matrix van orde 3:

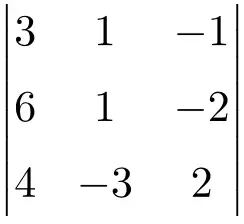
Opgeloste oefening van een determinant van een 3x3 matrix

zie oplossing

Om de oplossing van een determinant van een 3×3-matrix te vinden, moeten we de Sarrus-formule toepassen:

$\displaystyle\begin{aligned} \begin{vmatrix} 3 & 1 & -1 \\[1.1ex] 6 & 1 & -2 \\[1.1ex] 4 & -3 & 2 \end{vmatrix} & = \\ & = 3 \cdot 1 \cdot 2 + 1 \cdot (-2) \cdot 4 + 6 \cdot (-3) \cdot (-1) \ - \\[1.1ex] & \phantom{=} - 4 \cdot 1 \cdot (-1) - (-3) \cdot (-2) \cdot 3 - 6 \cdot 1 \cdot 2 \\[2.5ex] & =6 -8 +18 +4-18-12 \\[2.5ex] & = \bm{-10} \end{aligned}$

Oefening 5

vind de waarde van

$a$

waardoor de volgende determinant van de derde orde wordt geannuleerd:

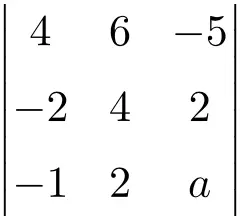
oefeningen stap voor stap opgelost voor determinanten van orde 3

zie oplossing

We berekenen eerst, met de regel van Sarrus, de waarde van de determinant als functie van

$a :$

$\displaystyle\begin{aligned}\begin{vmatrix} 4 & 6 & -5 \\[1.1ex] -2 & 4 & 2 \\[1.1ex] -1 & 2 & a \end{vmatrix} & = \\ & = 4 \cdot 4 \cdot a + 6 \cdot 2 \cdot (-1) + (-2) \cdot 2 \cdot (-5) \ - \\[1.1ex] & \phantom{=}- (-1) \cdot 4 \cdot (-5) - 2 \cdot 2 \cdot 4 - (-2) \cdot 6 \cdot a \\[2.5ex] & = 16a -12 + 20 - 20 - 16 +12a \\[2.5ex] & = 28a -28 \end{aligned}$

Om de determinant te laten verdwijnen, moet het resultaat 0 zijn. Daarom stellen we het resultaat gelijk aan 0 en lossen we de vergelijking op:

$28a-28=0$

$28a=28$

$a=\cfrac{28}{28} = \bm{1}$

Bereken de determinant van een 3×3-matrix met de regel van sarrus

Wat is de determinant van een 3×3-matrix?

Hoe bereken je een determinant van orde 3?

Sarrus-regel

Voorbeelden van 3×3 determinanten:

Opgeloste problemen van determinanten van 3 × 3 matrices

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren