Op deze pagina leggen we uit hoe je polynomen aftrekt. Daarnaast vindt u verschillende voorbeelden en opgeloste stapsgewijze oefeningen voor het aftrekken van polynomen.
Hoe polynomen aftrekken?
Om twee veeltermen van elkaar af te trekken, moet je de termen van de veeltermen die vergelijkbaar zijn, van elkaar aftrekken. Met andere woorden, het aftrekken van polynomen bestaat uit het aftrekken van termen die hetzelfde letterlijke deel hebben (dezelfde variabelen en dezelfde exponenten).
In de wiskunde kun je het aftrekken van polynomen op twee verschillende manieren berekenen: met de verticale methode of met de horizontale methode. Hieronder vindt u de uitleg van beide procedures, maar we raden u aan om eerst te leren hoe u polynomen verticaal kunt aftrekken en dan door te gaan naar de horizontale methode. Blijf uiteraard bij degene die u verkiest.
Aftrekken van verticale polynomen
Vervolgens zullen we zien hoe twee polynomen verticaal worden afgetrokken aan de hand van een voorbeeld:
- doe de aftrekking
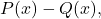
zijnde de twee polynomen:
![]()
![]()
Het eerste dat we moeten doen om een polynoomaftrekking te vinden, is door de ene polynoom onder de andere te plaatsen, zodat de soortgelijke termen van de twee polynomen in kolommen worden uitgelijnd:
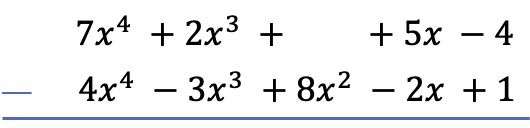
Waarschuwing: Als een polynoom geen term van een bepaalde graad heeft, moet de ruimte leeg worden gelaten. Bijvoorbeeld de polynoom
![]()
heeft geen kwadratische monomial, dus er is een lege ruimte op zijn plaats.
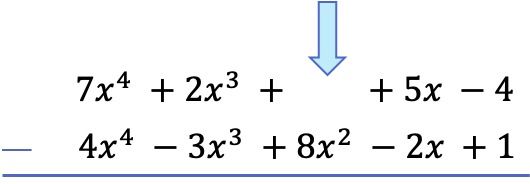
Hoewel we polynomen nu direct kunnen aftrekken, is het vrij gemakkelijk om het teken verkeerd te interpreteren als we het op deze manier doen. Om polynomen af te trekken, is het daarom het beste om het teken van alle termen in de aftrekkende polynoom (de aftrekkingspolynoom) te veranderen en vervolgens de optelling uit te voeren. Omdat het aftrekken van een polynoom hetzelfde is als het optellen van het tegenovergestelde polynoom.
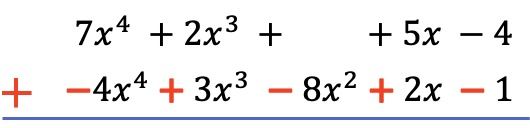
En zodra we alle termen in volgorde van de hoogste graad naar de laagste graad hebben gerangschikt en de termen van de onderstaande polynoom hebben ontkend, tellen we de coëfficiënten van elke kolom op, waarbij de letterlijke delen gelijk blijven:
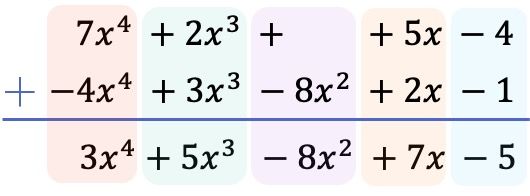
Daarom is het resultaat verkregen door het aftrekken van de 2 polynomen:
![]()
In het geval dat de laatste stap je niet duidelijk is, laat ik je de uitleg achter hoe het optellen van polynomen gebeurt. Het is in feite essentieel dat je het optellen van polynomen beheerst om succesvol polynomen af te kunnen trekken. Op de gelinkte pagina vind je ook voorbeelden en opgeloste oefeningen van het optellen van polynomen en daarnaast kun je de verschillen zien tussen het optellen en aftrekken van polynomen.
Aftrekken van horizontale polynomen
We hebben zojuist gezien hoe je polynomen verticaal kunt aftrekken, maar nu zullen we de andere methode zien die bestaat voor het aftrekken van polynomen: het horizontaal aftrekken van polynomen. Deze procedure is zeker sneller dan de vorige, maar het is noodzakelijk om de concepten van polynomen beter te beheersen.
Laten we dus aan de hand van een voorbeeld kijken waaruit deze methode voor het aftrekken van polynomen bestaat. En zodat je de verschillen tussen de twee methoden kunt zien, trekken we dezelfde polynomen af als in het vorige voorbeeld:
- Bereken de rest
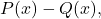
zijnde de twee polynomen:
![]()
![]()
We moeten de twee polynomen eerst in de vorm van een algebraïsche bewerking plaatsen, dat wil zeggen de een na de ander:
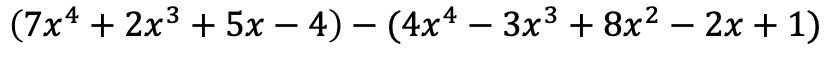
De monomialen tussen het eerste haakje blijven hetzelfde, maar de termen tussen het tweede haakje moeten van teken veranderen omdat ze een negatief ervoor hebben:
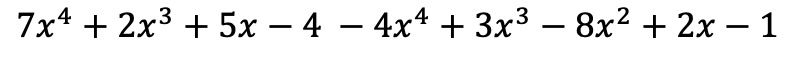
En nu groeperen we termen die identieke letterlijke delen hebben, dat wil zeggen termen met dezelfde variabelen (letters) en exponenten. Termen die niet op elkaar lijken, kunnen niet worden toegevoegd of verwijderd.
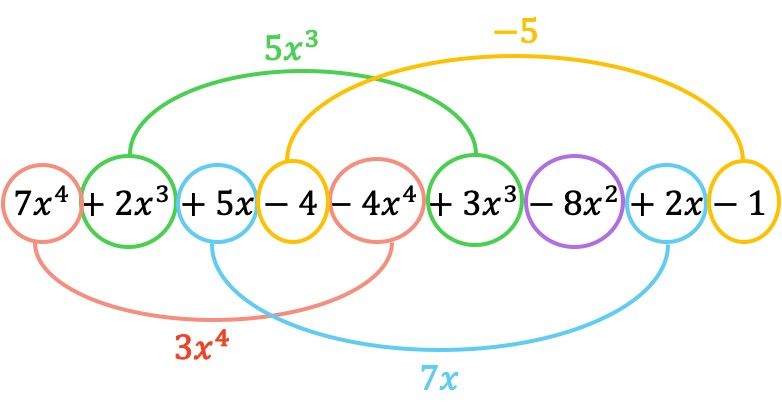
De polynoom die het resultaat is van de aftrekking is dus:
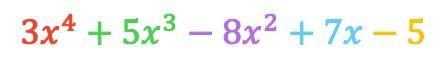
Zoals u kunt zien, hebben we met beide methoden hetzelfde resultaat bereikt, dus u kunt de methode gebruiken die het beste bij u past.
Nu je de twee methoden voor het oplossen van polynoomaftrekken hebt gezien, wist je dat je ook breuken met polynomen kunt aftrekken? En niet alleen aftrekkingen, maar allerlei soorten bewerkingen. Ontdek hoe bewerkingen worden uitgevoerd met algebraïsche breuken door op deze link te klikken.
Problemen met het aftrekken van polynomen opgelost
Zodat je kunt oefenen, laten we je een aantal opgeloste polynomiale aftrekkingsoefeningen achter. Als je vragen hebt over een oefening kun je deze stellen in de reacties op de pagina, wij zullen deze zo snel mogelijk beantwoorden.
Oefening 1
Trek de polynoom af
![]()
minus de polynoom
![]()
![]()
![]()
In dit geval trekken we de twee polynomen verticaal af. Om dit te doen, rangschikken we eerst de polynomen op graad, veranderen we vervolgens het teken van de resterende polynoomtermen en voegen we ten slotte de monomialen toe die zich in dezelfde kolom bevinden:
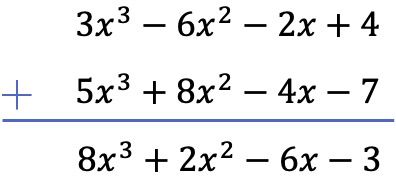
Oefening 2
Los het aftrekkingspolynoom op
![]()
minus de polynoom
![]()
![]()
![]()
Het aftrekken van twee polynomen komt neer op het optellen van het tegenovergestelde van het afgetrokken polynoom bij het verkleinwoordpolynoom. Daarom veranderen we het teken van de termen van de onderaannemingspolynoom (de resterende) en voegen we de polynomen toe:
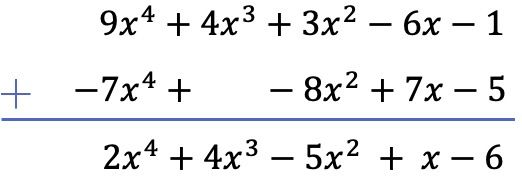
Merk op dat in dit specifieke geval een lege ruimte moet worden gelaten in de kolom van graad 3 van de tweede polynoom, aangezien deze geen term van de derde graad heeft.
Oefening 3
Zoek het resultaat van het aftrekken van de polynoom
![]()
minus de polynoom
![]()
![]()
![]()
In dit geval zullen we de aftrekking van de twee polynomen verticaal oplossen. Dus eerst plaatsen we de polynomen in volgorde van de grootste naar de kleinste graad, daarna veranderen we het teken van de termen van de resterende polynoom en tenslotte voegen we soortgelijke termen toe:
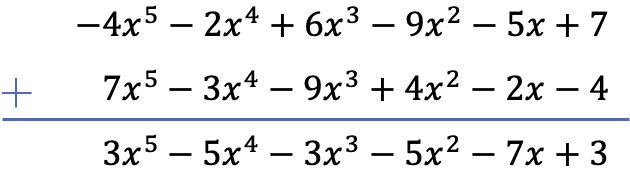
Oefening 4
Bereken de volgende bewerking met polynomen:
![]()
![]()
![]()
![]()
In dit geval zijn er 3 polynomen bij de bewerking betrokken, waarvan 2 aftrekkingen. Om de bewerking op te lossen, zullen we daarom het teken van alle termen van de twee resterende polynomen veranderen en vervolgens de polynomen optellen.
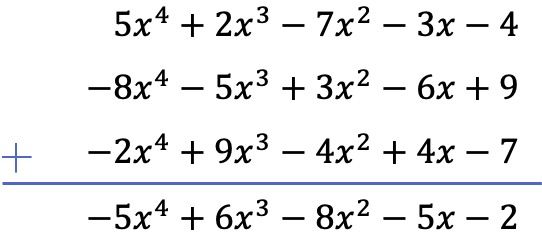
Wat vind jij van de uitleg? Vond je het nuttig? Welke methode voor het aftrekken van polynomen geeft u de voorkeur, verticaal of horizontaal? We lezen je in de reacties! 👀