Op deze pagina zullen we zien hoe je machten van matrices kunt gebruiken. Je vindt er ook voorbeelden en stap voor stap opgeloste oefeningen van machten van matrices die je zullen helpen het perfect te begrijpen. Ook leer je wat de n-de macht van een matrix is en hoe je deze kunt vinden.
Hoe wordt de kracht van een matrix berekend?
Om de macht van een matrix te berekenen, moet je de matrix zo vaak met zichzelf vermenigvuldigen als de exponent aangeeft. Bijvoorbeeld:
![]()
Om de kracht van een matrix te krijgen, moet je daarom weten hoe je matrixvermenigvuldiging oplost. Anders kun je geen machtsmatrix berekenen.
Voorbeeld van het berekenen van de kracht van een matrix:

Daarom wordt de kracht van een vierkante matrix berekend door de matrix met zichzelf te vermenigvuldigen. Op dezelfde manier is een kubusvormige matrix gelijk aan de vierkante matrix van de matrix zelf. Op dezelfde manier moet, om de macht te vinden van een matrix verhoogd tot vier, de matrix verhoogd tot drie worden vermenigvuldigd met de matrix zelf. Enzovoort.
Er is een belangrijke eigenschap van matrixmacht die u moet kennen: de macht van een matrix kan alleen worden berekend als deze vierkant is , dat wil zeggen als deze hetzelfde aantal rijen als kolommen heeft.
Wat is de macht n van een matrix?
De n-de macht van een matrix is een uitdrukking waarmee we eenvoudig elke macht van een matrix kunnen berekenen.
Vaak volgen de krachten van matrices een patroon . Als we de reeks die ze volgen kunnen ontcijferen, kunnen we dus elke macht berekenen zonder alle vermenigvuldigingen te hoeven doen.
Dit betekent dat we een formule kunnen vinden die ons de n-de macht van een matrix geeft zonder alle machten te hoeven berekenen.
Tips voor het ontdekken van het patroon gevolgd door de krachten:
- De pariteit van de exponent . Het kan zijn dat zelfs krachten de ene kant op gaan en oneven krachten de andere kant op.
- Variatie van tekens. Het kan bijvoorbeeld zijn dat elementen van even machten positief zijn en elementen van oneven machten negatief, of omgekeerd.
- Herhaling: of dezelfde matrix elk bepaald aantal machten wordt herhaald of niet.
- We moeten ook kijken of er een relatie bestaat tussen de exponent en de elementen van de matrix.
Voorbeeld van het berekenen van de macht n van een matrix:
- Zijn

bereken de volgende matrix
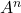
En
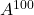
.
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60016ce1c6799c93007526681fbf4894_l3.png)
We zullen eerst een aantal machten van de matrix berekenen
![]()
, om te proberen het patroon te raden dat door de krachten wordt gevolgd. Dus wij berekenen
![]()
,
![]()
,
![]()
En
![]()
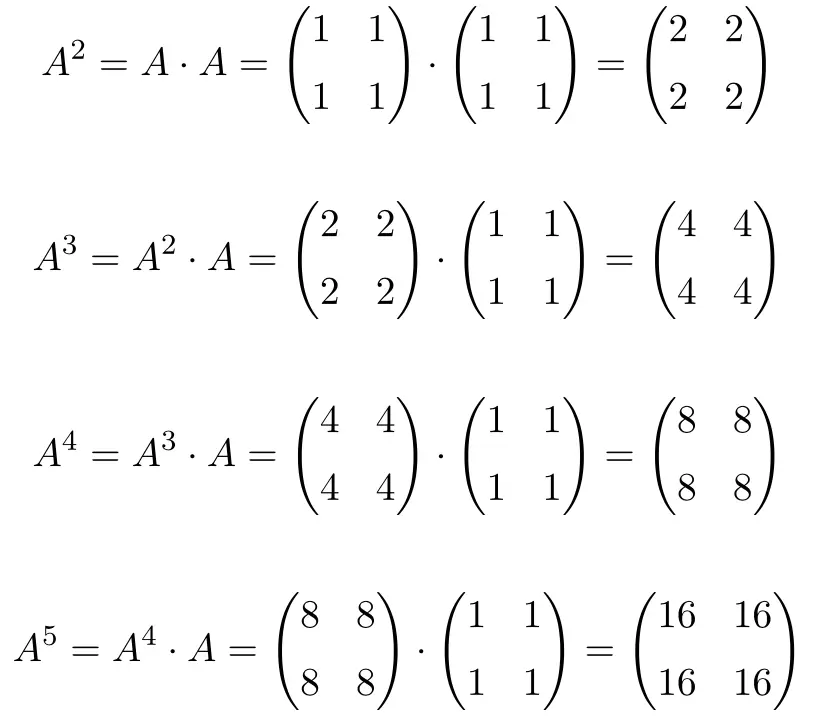
Bij het berekenen tot
![]()
, we zien dat de krachten van de matrix
![]()
Ze volgen een patroon: voor elke toename van het vermogen wordt het resultaat vermenigvuldigd met 2. Daarom zijn alle matrices machten van 2:
![Rendered by QuickLaTeX.com \displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ec7ee835cf9eda6a4f9d497e8baff79_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-69c6ff0f4de92192584dadc4719167c7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f724a50b220b3026d53e40ee17870359_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f08f7cc00465a6a098ce7d752aa66f_l3.png)
We kunnen daarom de formule voor de n-de macht van de matrix afleiden
![]()
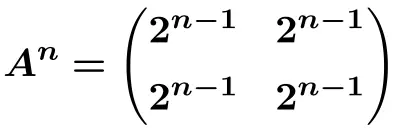
En met deze formule kunnen we berekenen
![]()
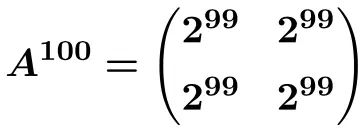
Matrixmachtsproblemen opgelost
Oefening 1
Beschouw de volgende matrix van afmeting 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdf81cf9fb956a144c7bda96a84ec7db_l3.png)
Berekenen:
![]()
Om de macht van een matrix te berekenen, moet je de matrix één voor één vermenigvuldigen. Daarom berekenen wij eerst
![]()
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24916b0b0e4431b0a2ee2b09875dc903_l3.png)
Nu gaan we berekenen
![]()
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57f79bd420c0044c84a64b431035b8ea_l3.png)
En tot slot gaan we rekenen
![]()
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bbc2ad8229ee141b323c9bbcc9df00fd_l3.png)
Oefening 2
Beschouw de volgende matrix van orde 2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33db03560b5c28f45eef9aa293484603_l3.png)
Berekenen:
![]()
![]()
is een te grote macht om met de hand te berekenen, dus de matrixmachten moeten een patroon volgen. Dus laten we berekenen
![]()
om te proberen de volgorde te begrijpen die ze volgen:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb9646cc984d754d2a618e6223e93cd3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22fdee28399b9115de98a214ba0c8473_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1a085a2338ce1e74885ca04bbd0011a7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dc357146829da8323a0755fa16a8ca8_l3.png)
Zo kunnen we het patroon zien dat de machten volgen: bij elke macht blijven alle getallen hetzelfde, behalve het element in de tweede kolom van de tweede rij, dat wordt vermenigvuldigd met 3. Daarom blijven alle getallen altijd hetzelfde. en het laatste element is een macht van 3:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a0bfa34768808832e0fd5d3f730eb27b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6e007f5ad5d38fd887d39f00bd2b9fc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-585d8a00f418b50f60b4f95d87c5839c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dec6b9db4b59d9759adf85cee442cca3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7244b46950df4d9107cbdb7ad004e17_l3.png)
Dus de formule voor de n-de macht van de matrix
![]()
Oosten:
![Rendered by QuickLaTeX.com \displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-beec2f1ed3e47902de0f25fe1901e294_l3.png)
En met deze formule kunnen we berekenen
![]()
![Rendered by QuickLaTeX.com \displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa3261646ca7bfa41f8ad46331a0af4b_l3.png)
Oefening 3
Beschouw de volgende 3×3-matrix:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f11fe8a7dcd1e308faa0af24eee3f362_l3.png)
Berekenen:
![]()
![]()
is een te grote macht om met de hand te berekenen, dus de matrixmachten moeten een patroon volgen. Dus laten we berekenen
![]()
om te proberen de volgorde te begrijpen die ze volgen:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acb15d7f461d11e3668bc0b96a1fdc06_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f416625ded948830fa80799249c12608_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a76fd60051b157f06c2a731ff575d1e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3409c7b8d82ffd21cc084a12405fce74_l3.png)
Zo kunnen we het patroon zien dat de machten volgen: bij elke macht blijven alle getallen hetzelfde, behalve breuken, die in de teller met één toenemen:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-86c72aa2b21e7a68bbebfe7af5daa420_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce805455e49bf018f8f22588391ac44c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd5468ece9001274493687f3786b0af3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-07fd0e03c0163b58fffbe0235009fd8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ea88723757d1f2d8d6de1ac2d3843c7_l3.png)
Dus de formule voor de macht van de n- de matrix
![]()
Oosten:
![Rendered by QuickLaTeX.com \displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56308ff348d67ba1aba5816d85e9ee1c_l3.png)
En met deze formule kunnen we berekenen
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5352f021f5ab30e999c57f978ff55ad6_l3.png)
Oefening 4
Beschouw de volgende matrix van maat 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4609248b534d656aa9495b58f42e343f_l3.png)
Berekenen:
![]()
![]()
is een te grote macht om met de hand te berekenen, dus de matrixmachten moeten een patroon volgen. In dit geval is het noodzakelijk om te berekenen
![]()
om de volgorde te kennen die ze volgen:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9a1fb4cf8bb75cf02d76a26054e6bfa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-110c4b30c78811cafdd4234e128ed414_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2b1976bbdf3c1daa9d75497efc07975c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e0266d832a2fc0a04c9f6582dc231d57_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21dea9844b7bfdb990bbb2bc955c866e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-788e75a71c1dfe4a60f0e52960715efe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4947286a163847383e3735a508b0037d_l3.png)
Met deze berekeningen kunnen we zien dat we voor elke vier machten de identiteitsmatrix krijgen. Dat wil zeggen dat het ons als resultaat de identiteitsmatrix van de machten zal opleveren
![]()
,
![]()
,
![]()
,
![]()
,… Dus om uit te rekenen
![]()
we moeten 201 ontbinden in veelvouden van 4:
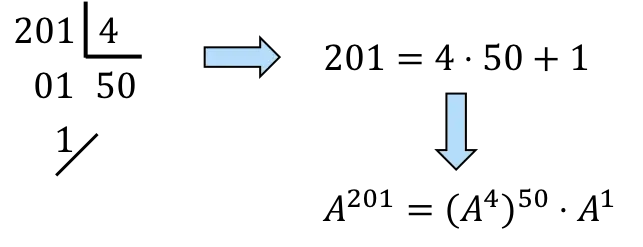
![]()
,Nog,
![]()
het zal 50 keer zijn
![]()
en eenmaal
![]()
![]()
En hoe weten wij dat
![]()
is de identiteitsmatrix
![]()
![]()
![]()
Bovendien geeft de identiteitsmatrix, verhoogd tot een willekeurig getal, de identiteitsmatrix. Nog:
![]()
En ten slotte geeft elke matrix vermenigvuldigd met de identiteitsmatrix dezelfde matrix. DUS:
![]()
Waarvoor
![]()
is gelijk aan
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1214abe876a5aede8fbbce79009d5dbc_l3.png)
Oefening 5
Beschouw de volgende matrix van orde 3:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f3ba8b2d15b622f99774be05aa2620_l3.png)
Berekenen:
![]()
Bereken uiteraard de kracht van de matrix
![]()
Dit is een te grote berekening om met de hand uit te voeren, dus de matrixmachten moeten een patroon volgen. In dit geval is het noodzakelijk om te berekenen
![]()
om de volgorde te kennen die ze volgen:
![Rendered by QuickLaTeX.com \displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4032b55d68a5615911a5b7c997b05e6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b5deef2a7728c5e82e1a1dafb1a939c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f62e856d037138b2ead39b17ccebf96d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854da5c09b6662da46acb790afb6d01a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9f804a1c129e18d105fb92254c971fa_l3.png)
Met deze berekeningen kunnen we zien dat we voor elke 3 machten de identiteitsmatrix verkrijgen. Dat wil zeggen dat het ons als resultaat de identiteitsmatrix van de machten zal opleveren
![]()
,
![]()
,
![]()
,
![]()
,…Dus dat is te berekenen
![]()
We moeten 62 ontbinden in veelvouden van 3:
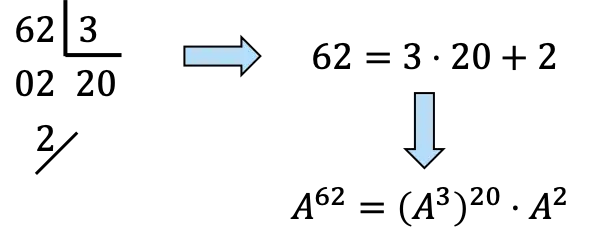
![]()
,Nog,
![]()
het zal 20 keer zijn
![]()
en eenmaal
![]()
![]()
En hoe weten wij dat
![]()
is de identiteitsmatrix
![]()
![]()
![]()
Bovendien geeft de identiteitsmatrix, verhoogd tot een willekeurig getal, de identiteitsmatrix. Nog:
![]()
Ten slotte geeft elke matrix vermenigvuldigd met de identiteitsmatrix dezelfde matrix. Nog:
![]()
Waarvoor
![]()
gelijk zal zijn aan
![]()
, waarvoor we eerder het resultaat hebben berekend:
![Rendered by QuickLaTeX.com \displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f95e17aacde501ca1c28dbf14324f0b_l3.png)
Als deze oefeningen over de machten van vierkante matrices nuttig voor je waren, kun je ook opgeloste stapsgewijze oefeningen vinden over het optellen en aftrekken van matrices , een van de meest gebruikte bewerkingen met matrices.