Matrixvermenigvuldiging

Op deze pagina zullen we zien hoe je matrices met de afmetingen 2×2, 3×3, 4×4, etc. kunt vermenigvuldigen . We leggen de matrixvermenigvuldigingsprocedure stap voor stap uit aan de hand van een voorbeeld, daarna vind je opgeloste oefeningen zodat je ook kunt oefenen. Ten slotte leer je wanneer twee matrices niet kunnen worden vermenigvuldigd en alle eigenschappen van deze matrixbewerking.

Hoe twee matrices te vermenigvuldigen?

Laten we de procedure bekijken om de vermenigvuldiging van twee matrices uit te voeren met een voorbeeld:

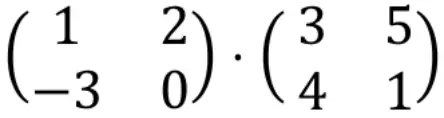
Om een matrixvermenigvuldiging te berekenen, moeten de rijen van de linkermatrix worden vermenigvuldigd met de kolommen van de rechtermatrix.

Dus eerst moeten we de eerste rij vermenigvuldigen met de eerste kolom. Om dit te doen, vermenigvuldigen we elk element in de eerste rij één voor één met elk element in de eerste kolom, en voegen we de resultaten toe. Dit alles zal dus het eerste element zijn van de eerste rij van de resulterende array. Kijk naar de werkwijze:

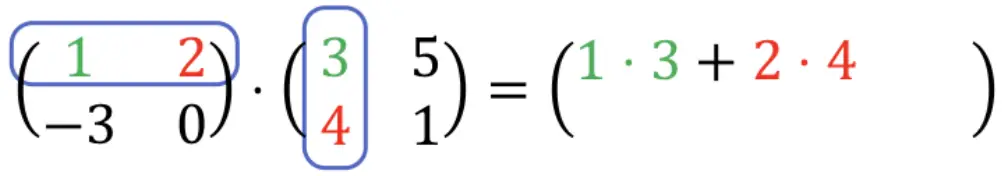
hoe je 2x2 matrixvermenigvuldiging oplost, bewerkingen met matrices

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Dus:

Nu moeten we de eerste rij vermenigvuldigen met de tweede kolom . We herhalen daarom de procedure: we vermenigvuldigen elk element van de eerste rij één voor één met elk element van de tweede kolom, en we tellen de resultaten op. En dit alles zal het tweede element zijn van de eerste rij van de resulterende array:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Dus:

Zodra we de eerste rij van de resulterende matrix hebben gevuld, gaan we naar de tweede rij. We vermenigvuldigen daarom de tweede rij met de eerste kolom door de procedure te herhalen: we vermenigvuldigen elk element van de tweede rij één met één met elk element van de eerste kolom, en tellen de resultaten op:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Nog:

Ten slotte vermenigvuldigen we de tweede rij met de tweede kolom . Altijd met dezelfde procedure: we vermenigvuldigen elk element van de tweede rij één voor één met elk element van de tweede kolom, en we tellen de resultaten op:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Nog:

En hier eindigt de vermenigvuldiging van de twee matrices. Zoals je hebt gezien, moet je de rijen met de kolommen vermenigvuldigen, waarbij je altijd dezelfde procedure herhaalt: vermenigvuldig elk element van de rij één voor één met elk element van de kolom, en tel de resultaten bij elkaar op.

Opgeloste matrixvermenigvuldigingsoefeningen

Oefening 1

Los het volgende matrixproduct op:

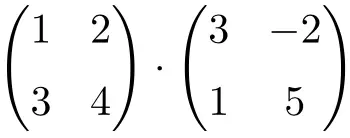
oefening stap voor stap opgelost product van 2x2 matrices, bewerkingen met matrices

zie oplossing

Het is een product van matrices van orde 2:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

Om een matrixproduct op te lossen, moet je de rijen van de linkermatrix vermenigvuldigen met de kolommen van de rechtermatrix.

Dus vermenigvuldigen we eerst de eerste rij met de eerste kolom. Om dit te doen, vermenigvuldigen we elk element in de eerste rij één voor één met elk element in de eerste kolom, en voegen we de resultaten toe. En dit alles zal het eerste element zijn van de eerste rij van de resulterende array:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Laten we nu de eerste rij vermenigvuldigen met de tweede kolom om het tweede element van de eerste rij van de resulterende matrix te verkrijgen:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

We gaan naar de tweede rij, dus vermenigvuldigen we de tweede rij met de eerste kolom:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Ten slotte vermenigvuldigen we de tweede rij met de tweede kolom om het laatste element van de tabel te berekenen:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

Het resultaat van matrixvermenigvuldiging is dus:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Oefening 2

Zoek het resultaat van de volgende 2×2 vierkante matrixvermenigvuldiging:

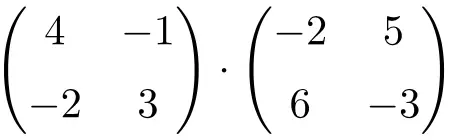
Oefening stap voor stap opgelost in 2x2 matrixvermenigvuldiging, matrixbewerkingen

zie oplossing

Het is een product van matrices met afmeting 2×2.

Om de vermenigvuldiging op te lossen, moet je de rijen van de linkermatrix vermenigvuldigen met de kolommen van de rechtermatrix:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Oefening 3

Bereken de volgende 3×3 matrixvermenigvuldiging:

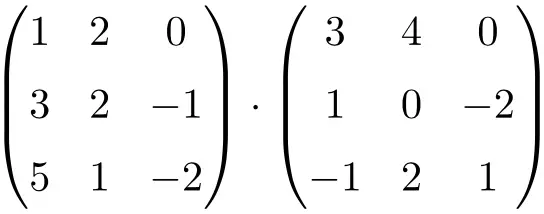
oefening opgelost stap voor stap vermenigvuldiging van 3x3 matrices, matrixbewerkingen

zie oplossing

Om een 3×3-matrixvermenigvuldiging uit te voeren, moet u de rijen van de linkermatrix vermenigvuldigen met de kolommen van de rechtermatrix:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Oefening 4

gegeven de matrix

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Berekenen:

$\displaystyle 2A\cdot A^t$

zie oplossing

We zullen eerst de getransponeerde matrix berekenen van

$A$

om de vermenigvuldiging te doen. En om de transponeermatrix te maken, moeten we de rijen in kolommen veranderen. Dat wil zeggen dat de eerste rij van de matrix de eerste kolom van de matrix wordt en de tweede rij van de matrix de tweede kolom van de matrix. Nog:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

De matrixbewerking blijft daarom:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Nu kunnen we de berekeningen doen. Wij berekenen eerst

$2A$

(hoewel we ook eerst kunnen berekenen

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

En ten slotte lossen we het product van matrices op:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Oefening 5

Beschouw de volgende matrices:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Berekenen:

$\displaystyle A\cdot B - B \cdot A$

zie oplossing

Het is een bewerking die aftrekken combineert met matrixvermenigvuldigingen van orde 2:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

We berekenen eerst de vermenigvuldiging aan de linkerkant:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Nu lossen we de vermenigvuldiging aan de rechterkant op:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

En tenslotte trekken we de matrices af:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

Wanneer kun je twee matrices niet vermenigvuldigen?

Niet alle matrices kunnen worden vermenigvuldigd. Om twee matrices te vermenigvuldigen, moet het aantal kolommen in de eerste matrix overeenkomen met het aantal rijen in de tweede matrix.

De volgende vermenigvuldiging kan bijvoorbeeld niet worden uitgevoerd omdat de eerste matrix 3 kolommen heeft en de tweede matrix 2 rijen:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

Maar als we de volgorde omdraaien, kunnen ze vermenigvuldigd worden. Omdat de eerste matrix twee kolommen heeft en de tweede matrix twee rijen:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

Eigenschappen van matrixvermenigvuldiging

Dit type matrixbewerking heeft de volgende kenmerken:

Matrixvermenigvuldiging is associatief:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

Matrixvermenigvuldiging heeft ook de distributieve eigenschap:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

Het product van matrices is niet commutatief:

$\displaystyle A \cdot B \neq B \cdot A$

De volgende matrixvermenigvuldiging geeft bijvoorbeeld een resultaat:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

Maar het resultaat van het product is anders als we de volgorde van vermenigvuldiging van de matrices omkeren:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

Bovendien resulteert elke matrix vermenigvuldigd met de identiteitsmatrix in dezelfde matrix. Dit wordt de multiplicatieve identiteitseigenschap genoemd:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

Bijvoorbeeld:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Ten slotte is, zoals je misschien al vermoedt, elke matrix vermenigvuldigd met de nulmatrix gelijk aan de nulmatrix. Dit wordt de multiplicatieve eigenschap van nul genoemd:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

Bijvoorbeeld:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

Matrix vermenigvuldiging

Hoe twee matrices te vermenigvuldigen?

Opgeloste matrixvermenigvuldigingsoefeningen

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Wanneer kun je twee matrices niet vermenigvuldigen?

Eigenschappen van matrixvermenigvuldiging

Laat een reactie achter Reactie annuleren