Op deze pagina zullen we zien hoe je een getal met een matrix kunt vermenigvuldigen. Je hebt ook voorbeelden waarmee je het perfect kunt begrijpen en opgeloste oefeningen zodat je kunt oefenen. Je vindt er ook alle eigenschappen van het product van een scalair en een matrix.
Hoe vermenigvuldig je een getal met een matrix?
Om een getal met een matrix te vermenigvuldigen , vermenigvuldigt u elk element van de matrix met dat getal.
Voorbeeld:

Problemen opgelost bij het vermenigvuldigen van een getal met een matrix
Oefening 1:
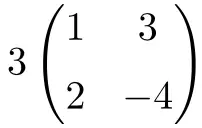
Het is een vermenigvuldiging van een scalair met een vierkante matrix van orde 2:
![Rendered by QuickLaTeX.com \displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-590b79c0fea524b963397181b6f2bea8_l3.png)
Oefening 2:
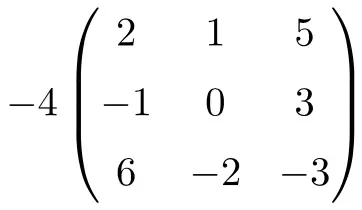
Het is een product van een getal door een vierkante matrix van orde 3:
![Rendered by QuickLaTeX.com \displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5042f0f8cd9b7a4d0e28974f793b145b_l3.png)
Oefening 3:
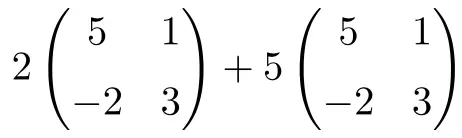
Het is een bewerking die producten van getallen door matrices en sommen van matrices met dimensie 2×2 combineert:
![Rendered by QuickLaTeX.com \displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56d2a40f021be13a5d92d0c10d353684_l3.png)
Daarom moeten we eerst voor producten het volgende oplossen:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-068901abef987767025bb01b24579226_l3.png)
En tenslotte voegen we de resulterende matrices toe:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d15ea16036f522af0f23fee0bb796757_l3.png)
Oefening 4:
Beschouw de volgende matrices:
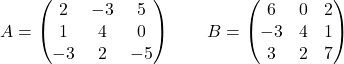
Berekenen:
![]()
Het is een operatie die scalaire vermenigvuldigingen combineert met optellingen en aftrekkingen van matrices met dimensie 3×3. Verder de matrix
![]()
is de identiteitsmatrix, die is samengesteld uit 1 op de hoofddiagonaal en 0 op de rest van de elementen:
![Rendered by QuickLaTeX.com \displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dce934040dc05714321dbbeac4e20c73_l3.png)
Daarom voeren we eerst de vermenigvuldigingen uit:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc26f29384abcfb6f08a36b601e4ff61_l3.png)
We voegen de eerste twee matrices toe:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-897ec02d46bc09bdec58d9b3246c6f4d_l3.png)
Ten slotte voeren we het aftrekken van de matrices uit:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ddd808a46a137f4c7742545c4f76f46_l3.png)
Als deze oefeningen over matrixproducten nuttig voor je waren, aarzel dan niet om te oefenen met de oefeningen die stap voor stap zijn opgelost over de optelling van matrices en het product van matrices , de twee soorten matrixbewerkingen die op meer worden herhaald.
Eigenschappen van het product van een getal door een matrix
Zoals u wel weet, zijn er vele soorten matrices : vierkante matrices, driehoekige matrices, de identiteitsmatrix, enz. Maar gelukkig zijn alle eigenschappen van het product van getallen in matrices geldig voor alle klassen matrices.
Hier zijn de eigenschappen van vermenigvuldiging tussen scalairen en matrices:
- Associatief eigendom:
![]()
Kijk eens naar de volgende twee bewerkingen, want ze geven hetzelfde resultaat, ongeacht hoe we de 2 en 3 vermenigvuldigen:
![Rendered by QuickLaTeX.com \displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4e9fd568edd5833238d8d21fdf4d1a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f8ee596b3e2ca16ff1c507717982ee1_l3.png)
- Distributieve eigenschap met betrekking tot de toevoeging van scalairen:
![]()
Zoals je in het onderstaande voorbeeld kunt zien, is het hetzelfde als we eerst 1+2 optellen en het vervolgens vermenigvuldigen met een matrix, of als we de matrix afzonderlijk vermenigvuldigen met 1 en met 2 en vervolgens de resultaten optellen:
![Rendered by QuickLaTeX.com \displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-025ac9b0851ed93fd0c3870328d6144b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2f54f4d5ae113e2462b752c150b3f43b_l3.png)
- Distributieve eigenschap met betrekking tot matrixoptelling:
![]()
Met andere woorden: het optellen van twee wiskundige matrices en het vervolgens vermenigvuldigen met een getal is gelijk aan het afzonderlijk vermenigvuldigen van de twee matrices met hetzelfde getal en het vervolgens optellen van de resultaten. In het onderstaande voorbeeld kunt u controleren:
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cdb35d5c66ee525c3d52fe7576e75758_l3.png)
![Rendered by QuickLaTeX.com \displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ef9d3f8f503371fa5f3d2478f728d88_l3.png)
- Eigenschap van het neutrale element:
![]()
Daarom wijzigen we de matrix niet als we een matrix met 1 vermenigvuldigen:
![Rendered by QuickLaTeX.com \displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ee2c0afd1bf2904722701caca883125_l3.png)
Dit zijn alle eigenschappen van het product van een scalair en een matrix, dus dat is het einde van dit artikel. We hopen dat je het leuk vond en vooral dat je hebt geleerd hoe je de vermenigvuldiging van getallen met matrices kunt oplossen.
Aan de andere kant zijn andere matrixbewerkingen die verband houden met vermenigvuldigen en die zeer nuttig zijn, bevoegdheden. Hier laten we u de pagina achter waar u leert wat het is en hoe u de kracht van een matrix kunt oplossen, voor het geval u nieuwsgierig bent.