Hoek tussen een lijn en een vlak

Hier ziet u hoe de hoek tussen een lijn en een vlak wordt berekend. Je zult ook voorbeelden kunnen zien en bovendien kunnen oefenen met stap voor stap opgeloste oefeningen van hoeken tussen lijnen en vlakken.

Wat is de hoek tussen een lijn en een vlak?

De hoek tussen een lijn en een vlak is de hoek tussen de lijn en zijn orthogonale projectie op het vlak.

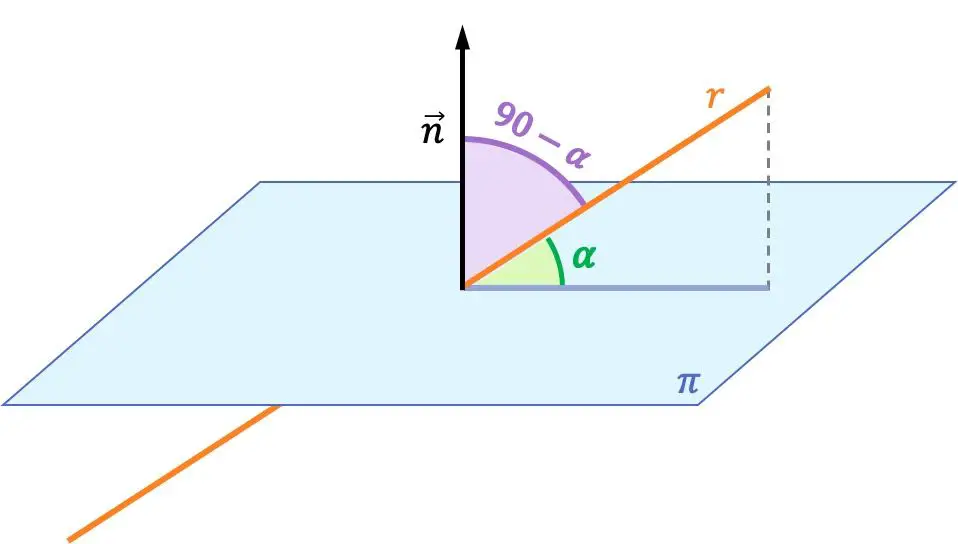
De hoek tussen een lijn en een vlak is het complement van de hoek tussen deze lijn en de vector loodrecht op het vlak. Daarom wordt de hoek tussen een lijn en een vlak berekend op basis van de hoek tussen de richtingsvector van de lijn en de normaalvector van het vlak.

Hoekformule tussen een lijn en een vlak

Om de formule voor de hoek tussen een vlak en een lijn af te leiden, moet je weten hoe je de hoek tussen twee vectoren kunt vinden . Op de gelinkte pagina vind je de uitleg en voorbeelden en oefeningen stap voor stap opgelost, dus als je niet meer weet hoe je het moet doen, raden we je aan om er eens naar te kijken.

Omdat de hoek tussen een lijn en een vlak dus complementair is aan de hoek tussen de richtingsvector van genoemde lijn

$(\vv{\text{v}}_r)$

en de normaalvector naar genoemd vlak

$(\vv{n})$

, uit de formule voor de hoek tussen twee vectoren leiden we af dat de hoek tussen een lijn en een vlak equivalent is aan de volgende uitdrukking:

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

Daarom is de formule voor de hoek tussen een lijn en een vlak :

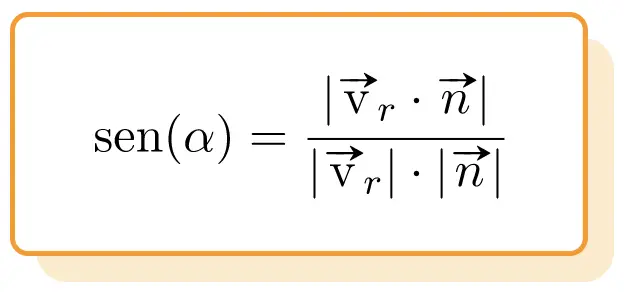
Goud:

$\vv{\text{v}}_r$

is de directe vector van de lijn.
$\vv{n}$

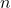
is de vector loodrecht op het vlak.

Voorbeeld van het berekenen van de hoek tussen een lijn en een vlak

Om u te laten zien hoe u dit soort problemen kunt oplossen, volgt hier een voorbeeld van het berekenen van de hoek tussen een lijn en een vlak:

Bereken de hoek gevormd door de lijn
$r$

met het vliegtuig

$\pi.$

Laat hun vergelijkingen zijn:

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

De lijn wordt uitgedrukt in de vorm van parametervergelijkingen, dus de richtingsvector is:

$\vv{\text{v}}_r = (-1,4,-3)$

Aan de andere kant wordt het vlak gedefinieerd in de vorm van een impliciete (of algemene) vergelijking, dus de normaalvector is:

$\vv{n} = (1,-1,4)$

Dus zodra we de richtingsvector van de lijn en de normaalvector van het vlak kennen, passen we de formule toe voor de hoek tussen een lijn en een vlak:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

We vervangen de vectoren in de formule:

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

En wij doen de berekeningen:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

Ten slotte keren we de sinus om met de rekenmachine en vinden we de waarde van de hoek:

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

De hoek tussen de lijn en het vlak is dus ongeveer 51,80º.

We moeten er rekening mee houden dat als we ooit een resultaat van 0° verkrijgen, dit betekent dat de lijn en het vlak evenwijdig zijn of dat de lijn in het vlak ligt. En als de hoek gelijk is aan 90º, betekent dit dat de lijn en het vlak loodrecht staan.

Problemen opgelost met de hoek tussen een lijn en een vlak

Oefening 1

Zoek de hoek gevormd door de lijn

$r$

met het vliegtuig

$\pi.$

Laat hun vergelijkingen zijn:

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

zie oplossing

De lijn wordt uitgedrukt als een continue vergelijking, dus de richtingsvector is:

$\vv{\text{v}}_r = (2,-1,-3)$

Aan de andere kant heeft het vlak de vorm van een impliciete (of algemene) vergelijking, dus de normaalvector is:

$\vv{n} = (3,1,2)$

Dus zodra we de richtingsvector van de lijn en de normaalvector van het vlak kennen, gebruiken we de formule voor de hoek tussen een lijn en een vlak:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

Ten slotte keren we de sinus om en vinden we de waarde van de hoek:

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

Daarom is de hoek tussen de lijn en het vlak 4,10 graden.

Oefening 2

Bepaal de hoek gevormd door de lijn

$r$

met het vliegtuig

$\pi.$

Laat hun vergelijkingen zijn:

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

zie oplossing

De lijn wordt uitgedrukt met zijn impliciete (of algemene) vergelijkingen. Het is daarom noodzakelijk om de richtingsvector van de lijn te vinden door het vectorproduct te berekenen van de vectoren loodrecht op de 2 vlakken die de lijn bepalen:

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

Aan de andere kant is de vector loodrecht op het vlak:

$\vv{n} = (-4,2,0)$

Dus zodra we de richtingsvector van de lijn en de normaalvector van het vlak kennen, gebruiken we de formule voor de hoek tussen een lijn en een vlak:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

Ten slotte keren we de sinus om en vinden we de waarde van de hoek:

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

Daarom is de hoek tussen de lijn en het vlak 46,33 graden.

Oefening 3

Vind met behulp van de formule voor de hoek tussen een lijn en een vlak de waarde van

$k$

noodzakelijk voor het recht

$r$

en het vliegtuig

$\pi$

evenwijdig zijn.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

zie oplossing

Eerst wordt de lijn uitgedrukt als een vectorvergelijking, dus de richtingsvector is:

$\vv{\text{v}}_r = (4,-1,3)$

Aan de andere kant heeft het vlak de vorm van een algemene vergelijking, dus de normaalvector is:

$\vv{n} = (4,3,k)$

Om de twee geometrische elementen evenwijdig te laten zijn, moet de hoek ertussen nul zijn. Daarom is de formule voor de hoek tussen een lijn en een vlak:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

Het puntproduct tussen de richtingsvector van de lijn en de normaalvector moet dus nul zijn. En uit deze vergelijking kunnen we de waarde van het onbekende bepalen

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

Ten slotte: als u dit artikel nuttig vond, bent u waarschijnlijk ook geïnteresseerd in hoe u de hoek tussen twee vlakken kunt vinden. Op de linkspagina vindt u een zeer gedetailleerde uitleg en de benodigde formule om de hoek tussen twee verschillende vlakken te berekenen en bovendien kunt u voorbeelden en oefeningen zien die stap voor stap zijn opgelost om te kunnen oefenen en begrijpen hoe het perfect gedaan wordt.

Wat is de hoek tussen een lijn en een vlak?

Hoekformule tussen een lijn en een vlak

Voorbeeld van het berekenen van de hoek tussen een lijn en een vlak

Problemen opgelost met de hoek tussen een lijn en een vlak

Oefening 1

Oefening 2

Oefening 3

Laat een reactie achter Reactie annuleren