Wat zijn vectoren (wiskunde)? -Mathoriteit

Op deze pagina vind je alles over vectoren: wat ze zijn, hun kenmerken, hoe ze berekend worden, hoe je bewerkingen met vectoren uitvoert, de verschillende soorten die er bestaan,…

Wat is een vector?

De wiskundige definitie van een vector is als volgt:

In de wiskunde is een vector een gericht segment dat van het ene punt (de oorsprong genoemd) naar een ander punt (het einde genoemd) gaat.

In de onderstaande grafiek ziet u bijvoorbeeld dat de vector

$\vv{AB}$

Het heeft punt A als oorsprong en punt B als eindpunt.

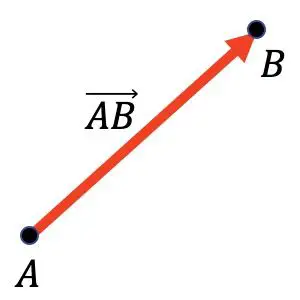
Vectoren worden voornamelijk gebruikt in de wiskunde, met name de meetkunde, en de natuurkunde, om vectorkrachten grafisch weer te geven.

Kenmerken van een vector

Als we eenmaal hebben gezien wat de wiskundige betekenis van vectoren is, gaan we nu kijken wat hun eigenschappen zijn.

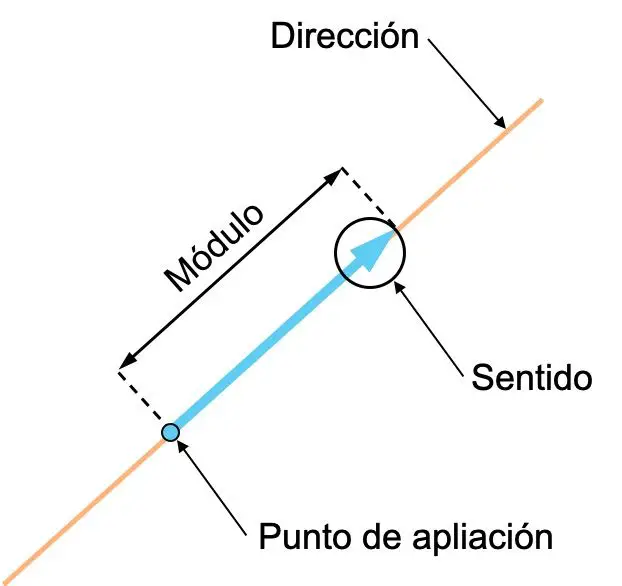
Elke vector heeft de volgende geometrische kenmerken:

Richting : De richting van een vector is de richting van de lijn die de vector bevat, of een lijn die evenwijdig daaraan loopt. Met andere woorden: de richting van een vector is de lijn waarop deze ligt.
Richting : de richting van een vector is de oriëntatie van de vector, aangegeven door zijn pijl.
Module (of grootte): de module van een vector is de lengte ervan en komt overeen met de numerieke waarde van de vector. Daarom geldt: hoe groter de vector betekent, hoe groter de vectorhoeveelheid die deze vertegenwoordigt.
Aanlegpunt : het aangrijpingspunt van een vector is de oorsprong van die vector.

De begrippen richting en richting van een vector zijn vaak verwarrend, dus het is belangrijk om het verschil daartussen te onderscheiden. Kijk naar het volgende voorbeeld met twee vectoren, beide hebben dezelfde richting, maar hun betekenis is verschillend:

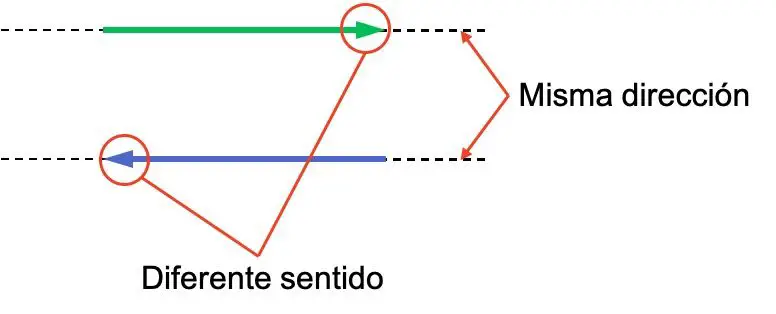
betekenis van de betekenis en richting van een vector

De twee vectoren hebben dezelfde richting omdat ze evenwijdig zijn. In plaats daarvan zijn hun richtingen tegengesteld omdat ze naar achteren gericht zijn.

Componenten van een vector

We hebben zojuist gezien dat vectoren grafisch worden weergegeven door pijlen, maar vectoren kunnen ook numeriek worden weergegeven door de componenten (of coördinaten) van een vector.

Als we bijvoorbeeld de volgende vector in een grafiek hebben weergegeven:

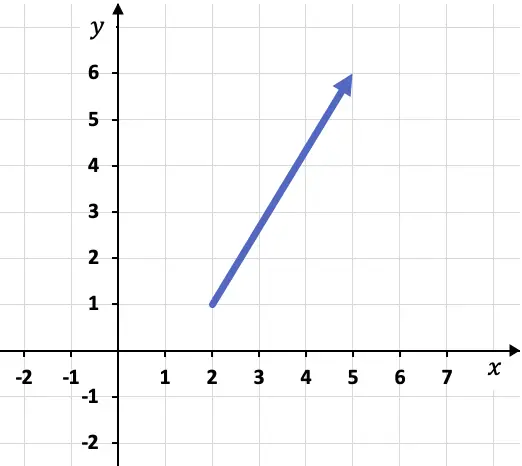
Om de componenten van de vector te berekenen, moeten we eerst de coördinaten van zijn oorsprong en einde identificeren, dat wil zeggen de punten waar hij begint en waar hij eindigt. In dit geval zijn de oorsprong en het einde van de vector:

Oorsprong van de vector: A(2,1)

Eindpunt van vector: B(5,6)

Om de coördinaten of componenten van de vector te vinden, trekt u eenvoudigweg het eindpunt minus de oorsprong af:

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

Zodat de componenten van de vector weergegeven in de grafiek zijn:

$\vv{\bm{AB}}\bm{=(3,5)}$

Vectoroperaties

vector toevoegen

Om twee vectoren numeriek op te tellen, moet u hun respectieve componenten optellen. Of met andere woorden: de X-coördinaten van de twee vectoren worden opgeteld en zijn dezelfde als de Y-coördinaten.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

Om te zien hoe dit wordt gedaan, voegen we de volgende twee vectoren toe:

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

Er kunnen ook twee vectoren worden toegevoegd vanuit hun grafische weergave. Hiervoor wordt normaal gesproken de parallellogramregel of -wet gebruikt, maar er zijn veel methoden. U kunt hier voorbeelden en opgeloste oefeningen zien over hoe u twee vectoren grafisch kunt toevoegen .

vectoraftrekking

Om twee vectoren analytisch af te trekken, moet u hun respectievelijke componenten van elkaar aftrekken. Dat wil zeggen dat de X-coördinaten van de twee vectoren van elkaar worden afgetrokken en hetzelfde zijn als de Y-coördinaten.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

Als voorbeeld trekken we de volgende twee vectoren af:

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

Net als bij optellen kun je ook 2 vectoren aftrekken met behulp van hun representaties. Hiervoor wordt meestal de driehoeksregel of wet gebruikt, maar er zijn verschillende methoden. Je kunt ze allemaal zien met voorbeelden en opgeloste oefeningen over hoe je twee vectoren grafisch van elkaar kunt aftrekken .

module van een vector

Zoals we aan het begin van deze pagina zagen, komt de grootte van een vector overeen met de lengte van die vector. Welnu, de lengte (of grootte) van een vector kan worden bepaald aan de hand van zijn componenten.

Overweeg elke vector:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Om de grootte van een vector in het vlak te vinden, moeten we de volgende formule toepassen:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

We berekenen bijvoorbeeld de grootte van de volgende vector met behulp van de formule:

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

Hoewel het heel eenvoudig lijkt, kan het bepalen van de grootte van een vector ingewikkeld zijn. Als je meer voorbeelden wilt zien en wilt oefenen met opgeloste oefeningen van de module van een vector , raden we je aan deze gelinkte pagina te bezoeken.

Vermenigvuldiging van een vector met een scalair

Om het product van een vector numeriek te berekenen met een getal (of een scalair), moet elke component van de vector met dat getal worden vermenigvuldigd.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

In het volgende algemene voorbeeld kunt u zien hoe de richting van de vector behouden blijft, ongeacht het teken van de scalaire waarde. Aan de andere kant hangt de richting van de vector af van het teken van het getal dat hij vermenigvuldigt.

vermenigvuldiging of product van een getal of scalair met een vector

Hieronder ziet u een numeriek voorbeeld van hoe u het product van een vector en een getal kunt vinden:

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

Scalair product

In de analytische meetkunde is het puntproduct een vectorbewerking die twee vectoren vermenigvuldigt en omzet in een reëel getal.

De formule voor het puntproduct van twee vectoren is dus als volgt:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

Hieronder heb je een voorbeeld waarbij het resultaat van het puntproduct tussen twee vectoren wordt berekend:

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

In deze link ziet u meer voorbeelden van het puntproduct . Daarnaast zul je een andere manier vinden om het puntproduct tussen twee vectoren te vinden, de eigenschappen van dit soort bewerkingen met vectoren en oefeningen stap voor stap opgelost.

vectorproduct

Hoewel ze qua naam erg op elkaar lijken, zijn het puntproduct en het kruisproduct totaal verschillend.

Kruisproduct , ook wel kruisproduct genoemd, is een bewerking tussen twee vectoren in de ruimte (in R3), dat wil zeggen dat het vectoren met drie coördinaten zijn.

Dus als we twee driedimensionale vectoren hebben:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Het kruisproduct van de twee vectoren is gelijk aan het resultaat van de volgende 3×3 determinant:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

waar de vectoren

$\vv{i}, \vv{j},\vv{k}$

zijn de eenheidsvectoren in respectievelijk de richtingen van de X-, Y- en Z-assen.

Bovendien staat de richting van de resulterende vector loodrecht op de twee vermenigvuldigde vectoren.

Zoals u kunt raden, is het oplossen van dit soort bewerkingen moeilijker dan de vorige en om deze reden hebben we een hele pagina met een gedetailleerde uitleg van hoe het kruisproduct tussen twee vectoren wordt berekend. Als u geïnteresseerd bent, raden wij u daarom aan deze te bezoeken en te oefenen met de opgeloste vectorproductoefeningen .

gemengd product

Het gemengde product van drie vectoren, ook wel het drievoudige puntproduct genoemd, is een opeenvolgende vermenigvuldiging tussen drie vectoren waarbij twee verschillende soorten bewerkingen betrokken zijn: het puntproduct en het vectorproduct. De combinatie van de twee vectorbewerkingen geeft dus een scalair (een reëel getal).

Concreet bestaat het gemengde product uit het berekenen van het vectorproduct van twee vectoren en het vervolgens vectorisch vermenigvuldigen van het resultaat dat wordt verkregen met een derde vector. Kijk naar de formule:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

Net als bij het vectorproduct is het oplossen van het gemengde product tussen vectoren niet eenvoudig. Om deze reden raden wij u aan om deze uitleg van het gemengde product van drie vectoren te bekijken, waar u voorbeelden, opgeloste oefeningen en de geometrische betekenis van deze vectorbewerking vindt.

vectortypen

Er zijn veel verschillende soorten vectoren, maar de belangrijkste definities die u moet kennen zijn:

Eenheidsvector : vector waarvan de module gelijk is aan 1.
Vaste vector : Een vector is vast wanneer de oorsprong van de vector op een vast punt wordt toegepast.
Vrije vector : Een vector is vrij als het toepassingspunt ervan niet gedefinieerd is, maar een vrij punt is.
Collineaire vectoren : twee of meer vectoren zijn collineair als ze dezelfde actielijn delen (lijn waar de vector zich bevindt).
Equivalente vectoren : twee vectoren zijn equipollen als ze dezelfde grootte, dezelfde betekenis en dezelfde richting hebben (hoewel ze verschillende aangrijpingspunten kunnen hebben).
Gekoppelde vectoren : Gekoppelde vectoren zijn equipollenvectoren die ook op dezelfde lijn werken.
Tegengestelde vectoren : twee vectoren zijn tegengesteld als ze dezelfde grootte en dezelfde richting hebben, maar een andere richting.
Positievector : de positievector is de vector waarvan de oorsprong het punt (0,0) is (oorsprong van de coördinaten).
Concurrerende vectoren : twee of meer vectoren zijn gelijktijdig wanneer hun actielijnen door hetzelfde punt gaan, dat wil zeggen dat ze elkaar snijden.
Parallelle vectoren : twee of meer vectoren zijn parallel als ze dezelfde richting hebben, ongeacht hun richting.
Loodrechte vectoren : Twee vectoren staan loodrecht (of orthogonaal) wanneer hun richtingen een hoek van 90° vormen.
Orthonormale vectoren : Twee of meer vectoren zijn orthonormaal als ze loodrecht op elkaar staan en bovendien unitair zijn (hun grootte is gelijk aan eenheid).
Coplanaire vectoren : twee of meer vectoren zijn coplanair als ze zich in hetzelfde vlak bevinden.

Hoek tussen twee vectoren

Om de hoek tussen twee gegeven vectoren te vinden, moeten we de volgende formule toepassen:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Goud

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

zijn de modules van de vectoren

$\vv{\text{u}}$

$\vv{\text{v}}$

respectievelijk.