Op deze pagina vindt u uitleg over wat een vlak is, hoe het berekend wordt en al zijn eigenschappen. Bovendien kunt u voorbeelden van vlakken zien, wat de relatieve posities tussen twee vlakken zijn, hoe u de hoek tussen 2 vlakken kunt bepalen en, ten slotte, hoe u elk vlak numeriek kunt uitdrukken met behulp van de vlakvergelijkingen.
Wat is een plan?
In analytische meetkunde is de definitie van het vlak als volgt:
Een vlak is een geometrisch object dat twee dimensies heeft (lengte en breedte).
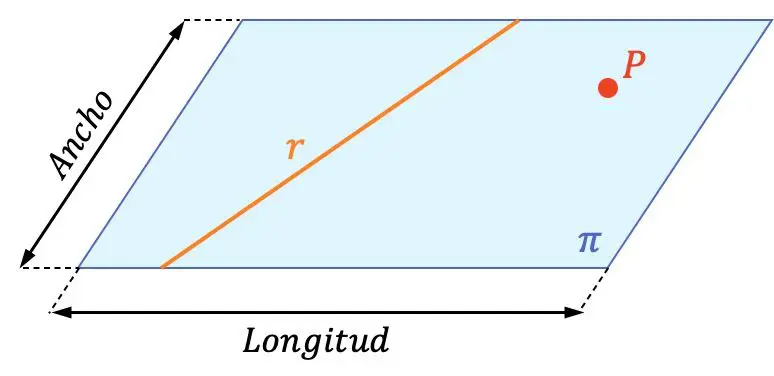
Daarom bevat een vlak oneindige lijnen en oneindige punten. In de grafische weergave hierboven zie je het verschil tussen een vlak, een lijn en een punt. U kunt ook verifiëren dat de lijn
![]()
en de tip
![]()
zitten in het vliegtuig
![]()
Zoals u in het getekende plan kunt zien, worden plannen meestal met Griekse letters genoemd:
![]()
Een voorbeeld van een vlak dat we veel gebruiken in de wiskunde is het cartesiaanse vlak. Het cartesiaanse vlak is het vlak dat wordt gedefinieerd door de abscis-as (X-as) en de ordinaat-as (Y-as). Een van de toepassingen van het cartesiaanse vlak is dat het wordt gebruikt om de positie van een object in een referentiesysteem te beschrijven.
Het bepalen van een plan
Nu we de betekenis van een vlak hebben gezien, gaan we kijken hoe elk vlak in de driedimensionale ruimte (in R3) kan worden bepaald.
Een plan wordt volledig bepaald door de volgende geometrische elementen:
- Drie punten niet op één lijn.
- Een rechte lijn en een punt naar buiten.
- Twee parallelle lijnen of twee snijdende lijnen.
Wat het laatste punt betreft: u weet waarschijnlijk al wat het betekent dat twee lijnen evenwijdig zijn. Maar de betekenis van snijlijnen is minder bekend, dus als je hier vragen hebt, kun je kijken wat snijlijnen zijn .
Als we aan een van de voorgaande drie voorwaarden voldoen, betekent dit dat we een plan kunnen opstellen.
eigenschappen plannen
Het plan voldoet aan de volgende kenmerken:
- Een vlak bevat een oneindig aantal punten.
- Een vlak bevat een oneindig aantal lijnen.
- Een vlak is onbeperkt, dat wil zeggen dat het een oppervlak is dat zich zonder grenzen in de ruimte uitstrekt.
- Twee snijdende vlakken bepalen een lijn.
- Een lijn die een punt in een vlak heeft, ligt daar niet noodzakelijkerwijs in. Om deel uit te maken van een vlak moet een lijn minstens twee punten in het vlak hebben.
- Oneindige vlakken kruisen een rechte lijn.
- Een halfvlak is elk van de twee delen waarin een vlak wordt verdeeld wanneer het door een van zijn lijnen wordt gesneden.
vlakke vergelijkingen
In de analytische meetkunde is de vergelijking van een vlak een vergelijking waarmee elk vlak wiskundig kan worden uitgedrukt. Om de vergelijking van een vlak te vinden heb je dus alleen een punt en twee lineair onafhankelijke vectoren nodig die bij dat vlak horen.

Zoals we hierboven zagen bij de uitleg van het begrip plan, zijn er echter verschillende manieren om een plan te bepalen. Welnu, op dezelfde manier zijn er ook verschillende manieren om een plan analytisch uit te drukken.
Alle soorten vergelijkingen van het vlak zijn dus: de vectorvergelijking , de parametrische vergelijkingen , de impliciete (of algemene) vergelijking en de canonieke (of segmentale) vergelijking van het vlak.
Dan zullen we in detail de uitleg en formule van alle vergelijkingen van het plan zien.
Vectorvergelijking van het vlak
Beschouw een punt en twee richtingsvectoren van een vlak:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
De formule voor de vectorvergelijking van een vlak is:
![]()
Of gelijkwaardig:
![]()
Goud
![]()
En
![]()
zijn twee scalairen, dat wil zeggen twee reële getallen.
Parametrische vergelijkingen van het vlak
De formule voor de parametervergelijking van een vlak is:
![]()
Goud:
-
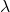
En
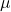
zijn twee scalairen, dat wil zeggen twee reële getallen.
-
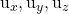
zijn de componenten van een van de twee leidende vectoren van het plan
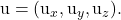
-
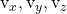
zijn de componenten van de andere sturende vector van het plan
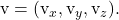
Impliciete of algemene vergelijking van het vlak
Beschouw een punt en twee richtingsvectoren van een vlak:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
De impliciete, algemene of cartesiaanse vergelijking van een vlak wordt verkregen door de volgende determinant op te lossen en het resultaat gelijk te stellen aan 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
De impliciete of algemene vergelijking van het resulterende plan zal dus als volgt zijn:
![]()
Dit type vlakvergelijking wordt ook wel cartesische vlakvergelijking genoemd.
Canonieke of segmentale vergelijking van het vlak
De formule voor de canonieke of segmentale vergelijking van een vlak is als volgt:
![]()
Goud:
-

is het snijpunt tussen het vlak en de X-as.
-

is het snijpunt tussen het vlak en de Y-as.
-

Dit is waar het vlak de Z-as snijdt.
De canonieke vergelijking (of segmentvergelijking) van het vlak kan ook worden verkregen uit de algemene vergelijking:
![]()
Eerst lossen we de coëfficiënt D op uit de vergelijking:
![]()
Vervolgens delen we de gehele vergelijking van het plan door de waarde van de parameter D veranderd van teken:
![]()
![]()
En door de eigenschappen van breuken te gebruiken, komen we tot de volgende uitdrukking:
![]()
We leiden daarom uit deze uitdrukking de formules af waarmee de termen van de canonieke of segmentale vergelijking van een vlak rechtstreeks kunnen worden berekend:
![]()
Om deze variant van de vergelijkingen van het plan te kunnen vormen, moeten de coëfficiënten A, B en C dus verschillend zijn van nul, waardoor onbepaalde breuken worden vermeden.
Relatieve positie van twee vlakken
In de analytische meetkunde zijn er slechts drie mogelijke relatieve posities tussen twee vlakken: snijvlakken, evenwijdige vlakken en samenvallende vlakken.
- Snijdende vlakken : Twee vlakken snijden elkaar als ze elkaar maar op één lijn snijden.
- Parallelle vlakken : Twee vlakken zijn evenwijdig als ze elkaar op geen enkel punt snijden.
- Samenvallende vlakken : Twee vlakken vallen samen als ze allemaal punten gemeenschappelijk hebben.
snijdende vlakken

parallelle vlakken

samenvallende vlakken

Bovendien, als twee elkaar snijdende vlakken elkaar kruisen onder een hoek van 90 graden, zijn het twee onderling loodrechte vlakken .
Hoek tussen twee vlakken
De hoek tussen twee vlakken is gelijk aan de hoek gevormd door de normaalvectoren van die vlakken. Om de hoek tussen twee vlakken te vinden, wordt daarom de hoek berekend die wordt gevormd door hun normaalvectoren, aangezien ze equivalent zijn.
Dus, als we eenmaal precies weten waaruit de hoek tussen twee vlakken bestaat, laten we dan eens kijken naar de formule voor het berekenen van de hoek tussen twee vlakken in de ruimte, die is afgeleid van de formule voor de hoek tussen twee vectoren:
Gegeven de algemene (of impliciete) vergelijking van twee verschillende vlakken:
![]()
![]()
De normaalvector van elk vlak is:
![]()
![]()
En de hoek gevormd door deze twee vlakken wordt bepaald door de hoek te berekenen die wordt gevormd door hun normaalvectoren met behulp van de volgende formule:
![]()
Het is duidelijk dat we, zodra we de cosinus van de hoek gevormd door de twee vlakken uit de formule hebben berekend, de cosinus moeten omkeren om de waarde van die hoek te vinden.
Aan de andere kant, wanneer de twee vlakken loodrecht of evenwijdig zijn, is het niet nodig om de formule toe te passen, omdat de hoek tussen de 2 vlakken rechtstreeks kan worden bepaald:
- De hoek tussen twee evenwijdige vlakken is 0°, omdat hun normaalvectoren dezelfde richting hebben.
- De hoek tussen twee loodrechte vlakken is 90º, omdat hun normaalvectoren ook loodrecht (of orthogonaal) op elkaar staan en dus een rechte hoek vormen.