Hier vindt u de formules voor alle soorten vergelijkingen van de lijn. Daarnaast kun je voorbeelden zien van hoe ze worden berekend en bovendien oefenen met opgeloste oefeningen van de vergelijkingen van de lijn.
Wat zijn alle vergelijkingen van de lijn?
Bedenk dat de wiskundige definitie van een lijn een reeks opeenvolgende punten is die in dezelfde richting worden weergegeven, zonder krommen of hoeken.
Om dus een rechte lijn in het vlak (in R2) analytisch uit te drukken, gebruiken we de vergelijkingen van de rechte lijn, en om ze te vinden heb je alleen een punt nodig dat bij de rechte lijn hoort en de richtingsvector van die rechte lijn. Met alleen deze twee geometrische elementen kun je absoluut alle verschillende vergelijkingen van de lijn vinden, die als volgt zijn:
De vergelijkingen van de lijn zijn de vectorvergelijking, de parametrische vergelijkingen, de continue vergelijking, de impliciete (of algemene) vergelijking, de expliciete vergelijking, de punt-hellingsvergelijking en de canonieke (of segmentale) vergelijking.
Alle soorten lijnvergelijkingen hebben hetzelfde doel: een lijn wiskundig weergeven. Maar elke vergelijking van de lijn heeft zijn eigen eigenschappen en daarom is het, afhankelijk van het probleem, beter om de een of de ander te gebruiken.

Nadat we het concept van lijnvergelijkingen hebben gezien, gaan we nu verder met het analyseren van de kenmerken van elk type lijnvergelijking in het bijzonder. Hieronder vindt u een gedetailleerde uitleg van de verschillende soorten vergelijkingen in de regel, maar als u wilt, kunt u direct naar het einde van de samenvattende tabel gaan met de formules van alle vergelijkingen in de regel .
Vectorvergelijking van de lijn
Ja
![]()
is de richtingsvector van de lijn en
![]()
een punt dat hoort bij rechts:
![]()
De formule voor de vectorvergelijking van de lijn is:
![]()
Goud:
-

En

zijn de cartesische coördinaten van elk punt op de lijn.
-

En

zijn de coördinaten van een bekend punt dat deel uitmaakt van de lijn

-

En

zijn de componenten van de richtingsvector van de lijn

-

is een scalair (een reëel getal) waarvan de waarde afhangt van elk punt op de lijn.
Het is de vectorvergelijking van de lijn in het vlak, dat wil zeggen bij het werken met punten en vectoren van 2 coördinaten (in R2). Als we echter berekeningen in de ruimte zouden uitvoeren (in R3), zouden we een extra component aan de vergelijking van de lijn moeten toevoegen:
![]()
Parametrische vergelijkingen van de lijn
De parametervergelijkingen van een lijn kunnen worden verkregen uit de vectorvergelijking:
![]()
We vermenigvuldigen eerst de parameter
![]()
door de richtingsvector van rechts:
![]()
Vervolgens voegen we de X- en Y-coördinaten toe:
![]()
En ten slotte verkrijgen we, door elke variabele afzonderlijk te wissen, de parametervergelijkingen van de lijn:
![]()
Goud:
-

En

zijn de cartesiaanse coördinaten van elk punt op de lijn.
-

En

zijn de coördinaten van een bekend punt dat deel uitmaakt van de lijn

-

En

zijn de componenten van de richtingsvector van de lijn

-

is een scalair (een reëel getal) waarvan de waarde afhangt van elk punt op de lijn.
Net als voorheen zijn dit de parametervergelijkingen van de lijn in het vlak (in R2), maar om de parametervergelijkingen van de lijn in de ruimte (in R3) te vinden zou het nodig zijn om nog een vergelijking toe te voegen voor de derde variabele Z:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e31f05449ce57a8af9ae4dda38535013_l3.png)
Continue vergelijking van de lijn
De continue vergelijking van elke lijn kan worden afgeleid uit de parametervergelijkingen:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-708dbb33878e2bab0dcc94c84f6ab670_l3.png)
Als we de instelling wissen
![]()
uit elke parametervergelijking verkrijgen we de volgende uitdrukkingen:
![]()
![]()
E Door de twee resulterende vergelijkingen gelijk te stellen, verkrijgen we de continue vergelijking van de lijn:
![]()
![]()
Kort gezegd is de continue vergelijking van de lijn :
![]()
Goud:
-

En

zijn de cartesiaanse coördinaten van elk punt op de lijn.
-

En

zijn de coördinaten van een bekend punt dat deel uitmaakt van de lijn

-

En

zijn de componenten van de richtingsvector van de lijn

Deze formule is voor de continue vergelijking van de lijn bij het werken in 2 dimensies (in 2D). Maar als we bewerkingen in 3 dimensies (3D) zouden uitvoeren, zouden we een extra component aan de lijnvergelijking moeten toevoegen:
![]()
Impliciete of algemene vergelijking van de lijn
Ja
![]()
is de richtingsvector van de lijn en
![]()
een punt dat hoort bij rechts:
![]()
De formule voor de impliciete, algemene of cartesiaanse vergelijking van de lijn is:
![]()
Goud:
-

En

zijn de cartesische coördinaten van elk punt op de lijn.
- de coëfficiënt

is de tweede component van de richtingsvector van de lijn:

- de coëfficiënt

is de eerste component van het richtingsvector veranderd teken:

- de coëfficiënt

wordt berekend door het bekende punt te vervangen

in de vergelijking van de lijn.
de formule kan de impliciete vergelijking van een lijn ook worden verkregen door de breuken van de continue vergelijking te vermenigvuldigen.
Expliciete vergelijking van de lijn
De formule voor de expliciete vergelijking van de lijn is:
![]()
Goud:
-

is de helling van de lijn.
-

het y-snijpunt, dat wil zeggen de hoogte waarop het de Y-as snijdt.
In het onderstaande gedeelte ziet u hoe de parameters worden bepaald
![]()
En
![]()
van de rechte lijn Maar een andere manier om de expliciete vergelijking te vinden is vooral het gebruik van de impliciete vergelijking; hiervoor moet het onbekende worden opgelost
![]()
van de impliciete vergelijking.
Betekenis van parameters m en n
Zoals we zagen bij de definitie van de expliciete vergelijking van de lijn, de parameter
![]()
is de helling van de lijn en
![]()
het y-snijpunt. Maar wat betekent dat? Laten we dit eens bekijken aan de hand van de grafische weergave van een lijn:

De term onafhankelijk
![]()
is het snijpunt van de lijn met de computeras (OY-as). Bijvoorbeeld in de bovenstaande grafiek
![]()
is gelijk aan 1 omdat de lijn de y-as snijdt op y=1.
Aan de andere kant, de term
![]()
geeft de helling van de lijn aan , dat wil zeggen de helling ervan. Zoals je in de grafiek ziet,
![]()
is gelijk aan 2 omdat de lijn 2 verticale eenheden stijgt voor 1 horizontale eenheid.
Het is duidelijk dat als de helling positief is, de functie toeneemt (omhoog), maar als de helling negatief is, neemt de functie af (omlaag).
Bereken de helling van een lijn
Als we eenmaal precies weten wat de helling van een lijn is, gaan we kijken hoe deze wordt berekend. Er zijn dus 3 verschillende manieren om de helling van een lijn numeriek te bepalen:
- Gegeven twee verschillende punten op de lijn

En

De helling van de lijn is gelijk aan:
- Ja

is de richtingsvector van de lijn, de helling is:
- Ja

is de hoek gevormd door de lijn met de abscis-as (X-as), de helling van de lijn is gelijk aan de raaklijn van genoemde hoek:
![]()
![]()
![]()

Punt-hellingvergelijking van de lijn
De formule voor de punt-hellingsvergelijking van de lijn is:
![]()
Goud:
-

is de helling van de lijn.
-

zijn de coördinaten van een punt op de lijn

Canonieke of segmentale vergelijking van de lijn
Hoewel deze variant van de vergelijking van de lijn minder bekend is, kan de canonieke vergelijking van de lijn worden verkregen uit de snijpunten van de lijn met de cartesische assen.
Laat de twee snijpunten met de assen van een gegeven lijn zijn:
Snijden met de X-as:
![]()
Snijden met Y-as:
![]()
De formule voor de canonieke vergelijking van de lijn is:
![]()

In de wiskunde wordt de canonieke vergelijking van de lijn ook wel een segmentvergelijking of symmetrische vergelijking genoemd.
Aan de andere kant de coëfficiënten
![]()
En
![]()
Ze kunnen ook worden gevonden uit de algemene vergelijking van de lijn met behulp van de volgende formules:
![]()
![]()
Alle vergelijkingen van de lijn (formules)
Samenvattend is hier een tabel met de formules van alle vergelijkingen van de lijn:

Voorbeeld van het berekenen van vergelijkingen van de lijn
Nu we de hele uitleg van de vergelijking van de lijn hebben gezien, gaan we kijken hoe een typisch probleem van vergelijkingen van de lijn wordt opgelost:
- Zoek alle vergelijkingen van de lijn bepaald door het punt

en de vector
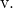
![]()
Allereerst vinden we de vectorvergelijking van de lijn uit de formule:
![]()
Vervang eenvoudigweg de coördinaten van het punt en de vector in de formule:
![]()
Ten tweede vinden we de parametervergelijkingen van de lijn via de overeenkomstige formule:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b4690a2ab033a4016f2d16b9554ddea_l3.png)
En we bepalen ook de continue vergelijking van de lijn met zijn formule:
![]()
![]()
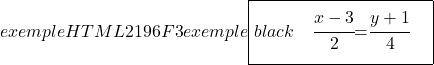
Zoals je hebt gezien zijn vector-, parametrische en continue vergelijkingen eenvoudig te berekenen; je hoeft alleen maar de bijbehorende formules te gebruiken.
Laten we nu verder gaan met het vinden van de algemene (of impliciete) vergelijking van de lijn. Om dit te doen kruisen we de twee breuken van de continue vergelijking:
![]()
![]()
![]()
![]()
Nu kunnen we de expliciete vergelijking van de lijn bepalen die het onbekende oplost
![]()
van de impliciete vergelijking:
![]()
![]()
![]()
![]()
Daarom is de helling van de lijn gelijk aan 2 (term die bij de onafhankelijke variabele hoort
![]()
).
![]()
En hiermee kunnen we de punt-hellingsvergelijking van de lijn berekenen met de formule:
![]()
![]()
![]()
Om ten slotte de segmentvergelijking van de lijn te vinden, berekenen we de snijpunten met de assen OX en OY en passen we de formule toe:
![]()
Snijpunt met de abscis-as (X-as)
![]()
![]()
![]()
![]()
![]()
Snijpunt met de y-as (Y-as)
![]()
![]()
![]()
![]()
![]()
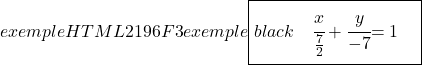
vergelijking van een rechte lijn die door twee punten gaat
Een ander veel voorkomend probleem bij lijnvergelijkingen is het vinden van de vergelijking van de lijn die wordt bepaald door twee gegeven punten. Hoewel we de richtingsvector van de lijn kunnen berekenen met de 2 punten en vervolgens de vergelijking, geven we u hieronder een formule waarmee u direct en eenvoudig de vergelijking van genoemde lijn kunt vinden.
Beschouw twee punten op een lijn:
![]()
De formule om de vergelijking van de lijn vanuit de twee punten te vinden is:
![]()
Met deze formule kunnen we rechtstreeks de punt-hellingsvergelijking van de lijn berekenen als we 2 punten krijgen waar de lijn doorheen gaat.
Opgeloste problemen van vergelijkingen van de lijn
Oefening 1
Zoek de vectorvergelijking, parametervergelijkingen en continue vergelijking van de lijn die door het punt wordt gedefinieerd
![]()
en zijn richtvector
![]()
Wees beide:
![]()
Eerst berekenen we de vectorvergelijking van de lijn op basis van de formule:
![]()
![]()
Vervolgens vinden we de parametervergelijkingen van de lijn met behulp van de bijbehorende formule:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a734c32ae40ca816c19b895e54916eb4_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-bff16cf5ab85c87d8a866a2d74ea2a31_l3.png)
En ten slotte bepalen we de continue vergelijking van de lijn met de bijbehorende formule:
![]()
![]()
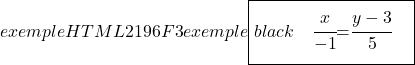
Oefening 2
Zoek de impliciete vergelijking, expliciete vergelijking en punt-hellingvergelijking van de lijn bepaald door het punt
![]()
en zijn richtingsvector is
![]()
![]()
De formule voor de impliciete vergelijking van de lijn is:
![]()
We moeten daarom de coëfficiënten A, B en C vinden. De onbekenden A en B worden verkregen uit de coördinaten van de richtingsvector van de lijn, omdat de volgende gelijkheid altijd wordt geverifieerd:
![]()
Bijgevolg is de coëfficiënt A de tweede coördinaat van de vector, en de coëfficiënt B de eerste coördinaat van het vectorgewijzigde teken:
![Rendered by QuickLaTeX.com \left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9357fbcba6acde824f0fa1cc3e389a0c_l3.png)
Daarom hoeven we alleen de coëfficiënt C te vinden. Om dit te doen, moeten we het punt waarvan we weten dat het bij de lijn hoort, in de vergelijking vervangen:
![]()
![]()
![]()
![]()
![]()
Dus de impliciete, algemene of cartesiaanse vergelijking van de lijn is:
![]()
Nu kunnen we de expliciete vergelijking van de lijn bepalen die het onbekende oplost
![]()
van de impliciete vergelijking:
![]()
![]()
![]()
![]()
Daarom is de helling van de lijn gelijk aan 3 (term vóór de onafhankelijke variabele
![]()
).
![]()
En uit de waarde van de helling van de lijn kunnen we de punt-hellingsvergelijking van de lijn berekenen met de formule:
![]()
![]()
![]()
Oefening 3
Bepaal 3 punten op de volgende lijn, uitgedrukt als een impliciete of algemene vergelijking:
![]()
Om een punt op een lijn te berekenen, hoeven we alleen maar een waarde aan een van de variabelen toe te kennen en vervolgens de waarde van de andere variabele op dat punt te vinden.
Een eerste punt berekenen we door te doen
![]()
![]()
![]()
![]()
![]()
![]()
We vinden dan een tweede punt dat een andere waarde aan de variabele geeft
![]()
Bijvoorbeeld
![]()
![]()
![]()
![]()
![]()
![]()
![]()
En ten slotte berekenen we een derde punt door op te lossen
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Oefening 4
Zoek alle vergelijkingen van de lijn die door het punt wordt gedefinieerd
![]()
en de vector
![]()
![]()
Allereerst vinden we de vectorvergelijking van de lijn uit de formule:
![]()
![]()
Ten tweede vinden we de parametervergelijkingen van de lijn via de overeenkomstige formule:
![Rendered by QuickLaTeX.com \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d2e6878c4d9b80337639f5fa7728a9f9_l3.png)
![Rendered by QuickLaTeX.com \definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3bf46da9a68147118874a619f918077_l3.png)
En we bepalen ook de continue vergelijking van de lijn met behulp van de formule:
![]()
![]()
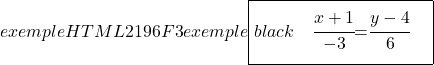
Laten we nu verder gaan met het vinden van de impliciete of algemene vergelijking van de lijn. Om dit te doen kruisen we de twee breuken van de continue vergelijking:
![]()
![]()
![]()
![]()
Nu kunnen we de expliciete vergelijking van de lijn bepalen die het onbekende oplost
![]()
van de impliciete vergelijking:
![]()
![]()
![]()
![]()
Daarom is de helling van de lijn gelijk aan -2 (term die bij de onafhankelijke variabele hoort
![]()
).
![]()
En hiermee kunnen we de punt-hellingsvergelijking van de lijn berekenen met de formule:
![]()
![]()
![]()
Om ten slotte de segmentvergelijking van de lijn te vinden, berekenen we de snijpunten van de lijn met de assen OX en OY en gebruiken we vervolgens de formule:
![]()
Snijpunt met de abscis-as (X-as)
![]()
![]()
![]()
![]()
![]()
Snijpunt met de y-as (Y-as)
![]()
![]()
![]()
![]()
![]()
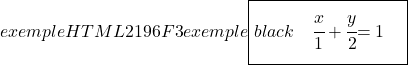
Oefening 5
Zoek de vergelijking van de lijn die door de volgende twee punten gaat:
![]()
Omdat we al twee punten op de lijn kennen, passen we de formule voor de vergelijking van de lijn rechtstreeks toe op 2 gegeven punten:
![]()
Nu vervangen we de cartesiaanse coördinaten van de punten in de formule:
![]()
En ten slotte berekenen we de helling van de lijn:
![]()
![]()
De vergelijking van de lijn die door deze twee punten gaat, is daarom:
![]()