Op deze pagina leert u wat coplanaire vectoren zijn en hoe u kunt bepalen of 2, 3, 4 of meer vectoren coplanair zijn. Bovendien kunt u voorbeelden en oefeningen zien die stap voor stap zijn opgelost met coplanaire vectoren.
Wat zijn coplanaire vectoren?
In de analytische meetkunde is de betekenis van coplanaire (of coplanaire) vectoren als volgt:
Coplanaire vectoren zijn vectoren die tot hetzelfde vlak behoren.
Daarom zijn twee vectoren altijd coplanair omdat een vlak kan worden gevormd met slechts twee vectoren. Aan de andere kant, als er 3, 4 of meer vectoren zijn, is het mogelijk dat een van de vectoren zich niet in hetzelfde vlak bevindt en daarom niet coplanair is.
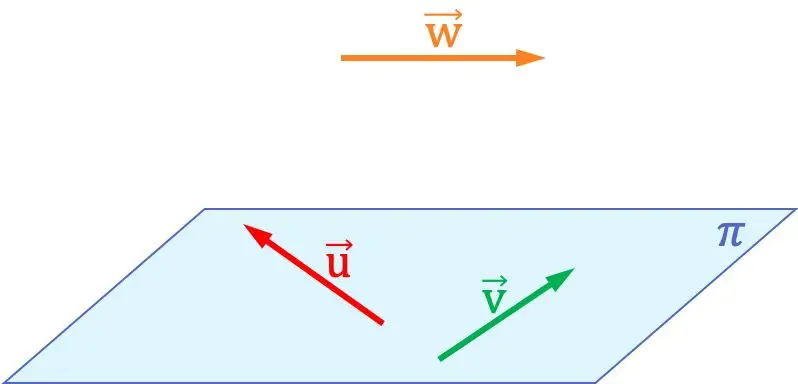
In de grafiek hierboven kun je bijvoorbeeld zien dat de vectoren
![]()
En
![]()
ze liggen in één vlak met elkaar, omdat ze zich in hetzelfde vlak bevinden. Aan de andere kant zijn deze twee vectoren niet coplanair met de vector
![]()
, omdat er geen vlak kan worden gevormd in de ruimte die de drie vectoren bevat.
Uit deze eigenschap kunnen we afleiden dat als 3 of meer vectoren coplanair zijn, de punten die deze vectoren definiëren (begin en einde van de vector) ook coplanaire punten zijn.
Wanneer zijn vectoren coplanair?
Zoals we hebben gezien bij de definitie van coplanaire (of coplanaire) vectoren, zijn twee vectoren altijd coplanair, maar hoeven meer dan twee vectoren de coplanariteitsrelatie niet te respecteren.
Er zijn dus verschillende methoden om te bepalen of drie of meer vectoren coplanair zijn:
- Als het gemengde product van drie vectoren (of het drievoudige puntproduct) gelijk is aan nul, betekent dit dat de drie vectoren coplanair zijn. Als het u niet helemaal duidelijk is hoe deze bewerking wordt berekend, raad ik u aan om te kijken naar wat het gemengde product is van drie vectoren . Hier vindt u de uitleg, evenals voorbeelden en opgeloste oefeningen.
![]()
- Als een reeks vectoren kan worden uitgedrukt als een lineaire combinatie van twee vectoren, impliceert dit dat ze coplanair zijn, wat betekent dat 3 of meer vectoren coplanair zijn als en slechts als ze lineair afhankelijk zijn. Om aan te tonen dat drie of meer vectoren een lineaire combinatie van twee vectoren zijn, volstaat het dat de rangorde van de matrix gevormd door alle vectoren gelijk is aan 2.
![]()
Het is belangrijk dat je een goed begrip hebt van het concept van lineaire afhankelijkheid en onafhankelijkheid , dat wil zeggen wanneer twee vectoren lineair afhankelijk of lineair onafhankelijk zijn, en wat dat betekent. Mocht het je niet helemaal duidelijk zijn, dan vind je in de link een zeer gedetailleerde uitleg, waarbij je bovendien voorbeelden en oefeningen stap voor stap opgelost ziet.
- Als de vectoren in kwestie parallelle vectoren zijn, betekent dit dat ze ook coplanair zijn, dat wil zeggen dat alle parallelle vectoren zich in hetzelfde vlak bevinden.
![]()
Opgeloste problemen van coplanaire vectoren
Oefening 1
Bepaal of de volgende drie vectoren coplanair zijn:
![]()
![]()
![]()
Om te controleren of dit 3 coplanaire vectoren zijn, moeten we het gemengde product tussen de drie vectoren berekenen:
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a1e4b0655c0a3f0165c880f5e64cce0_l3.png)
Het gemengde product van de drie vectoren is nul, dus de 3 vectoren zijn coplanair .
Oefening 2
Bepaal of de volgende drie vectoren coplanair zijn:
![]()
![]()
![]()
Eén manier om te controleren of we met drie coplanaire vectoren te maken hebben, is door het gemengde product tussen de drie vectoren op te lossen. Als we echter goed naar de componenten van de vectoren kijken, kunnen we zien dat ze proportioneel zijn. Daarom zijn de drie vectoren evenwijdig aan elkaar.
![]()
En aangezien alle vectoren evenwijdig zijn, zijn het in feite drie coplanaire vectoren .
Oefening 3
Bepaal of de volgende vier vectoren coplanair zijn:
![]()
![]()
![]()
![]()
Om te weten of de vier vectoren coplanair zijn, moeten we de rangorde berekenen van de matrix die uit alle vectoren bestaat:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8384924c86edafd568505d5f80e1705d_l3.png)
In dit geval berekenen we de reikwijdte van genoemde matrix aan de hand van determinanten:
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2778435c7f53952adf072419af8b268c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-82f278494a221879cc86da92ab4378c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-889142ac348173dd6c838633007f2d06_l3.png)
![]()
De rangorde van de matrix gevormd door alle vectoren is gelijk aan 2, daarom zijn de 4 vectoren coplanair .
Oefening 4
Bereken parameterwaarde
![]()
zodat de volgende 4 punten coplanair zijn:
![]()
![]()
![]()
![]()
Om de vier punten coplanair te laten zijn, moeten de daardoor bepaalde vectoren coplanair zijn. We berekenen daarom deze vectoren:
![]()
![]()
![]()
Wiens vectormatrix is:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
Om de resulterende vectoren coplanair te laten zijn, moet de rangorde van de matrix 2 zijn. En daarom moet de determinant van de gehele 3×3-matrix 0 zijn:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
Eindelijk lossen we het onbekende op
![]()
![]()
![]()