Op deze pagina ontdek je wat het betekent als twee lijnen coplanair zijn. Je zult ook kunnen zien wanneer twee lijnen coplanair zijn en daarnaast vind je voorbeelden en opgeloste oefeningen van coplanaire lijnen.
Wat zijn twee coplanaire lijnen?
In analytische meetkunde is de definitie van coplanaire lijnen als volgt:
Twee lijnen zijn coplanair als ze zich in hetzelfde vlak bevinden. Daarom kunnen coplanaire lijnen alleen secanslijnen , parallelle lijnen of samenvallende lijnen zijn.
Bovendien zijn twee coplanaire lijnen voldoende om een vlak volledig te definiëren. Hoewel een vlak uiteraard meer dan twee coplanaire lijnen kan hebben, bevat elk vlak in feite een oneindig aantal lijnen.
Aan de andere kant, als twee lijnen niet coplanair zijn, betekent dit dat ze elkaar snijden.
Voorbeelden van coplanaire lijnen
Om het concept van coplanaire lijnen beter te begrijpen, is hier een voorbeeld met drie lijnen:
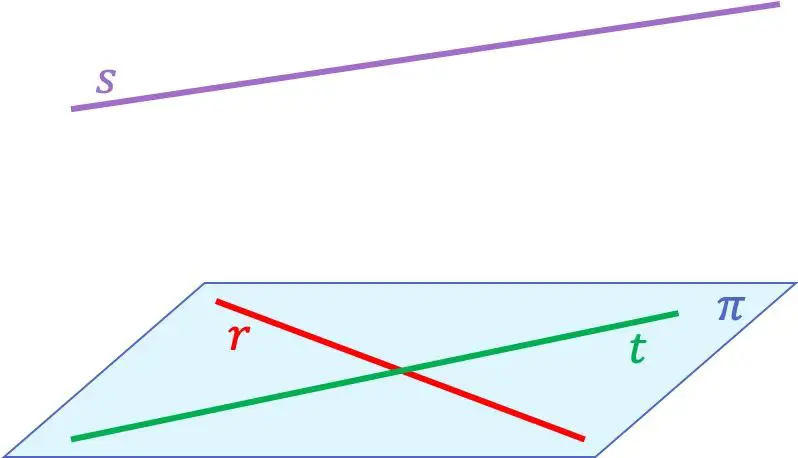
In dit geval de lijnen
![]()
En
![]()
Ze zijn coplanair omdat ze tot hetzelfde vlak behoren. In plaats daarvan de rechte lijn
![]()
ligt niet in één vlak met een van de andere twee lijnen, aangezien het de lijnen snijdt
![]()
En
![]()
Hoe weet je of twee lijnen coplanair zijn?
Zoals we hierboven zagen bij de uitleg van coplanaire lijnen, kunnen dit alleen secansvormige, evenwijdige of samenvallende lijnen zijn. Met andere woorden: twee gekruiste lijnen zullen nooit coplanair zijn.
Om te weten of twee lijnen in één vlak liggen, moet de relatieve positie daartussen worden bepaald. Als het twee elkaar snijdende, evenwijdige of samenvallende lijnen zijn, betekent dit dat het coplanaire lijnen zijn.
Om de coplanariteit van twee lijnen te controleren, moet u dus eerst weten hoe u de relatieve positie van twee lijnen in de ruimte kunt berekenen . Als je nog niet bekend bent met dit concept, kun je het beste eerst de link bekijken, waar je de volledige uitleg vindt, maar ook voorbeelden, oefeningen en opgeloste problemen.
Opgeloste oefening van coplanaire lijnen
Als voorbeeld zullen we een typische oefening op coplanaire lijnen oplossen:
- Bepaal of de volgende twee lijnen al dan niet coplanair zijn:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=4t \\[1.7ex] z=5 \end{cases} \qquad \qquad s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76e57f7dd2bfa67f2cf4eb2ee0455dcf_l3.png)
Het eerste wat we moeten doen is de relatieve positie tussen de twee lijnen vinden en hiervoor moeten we beide met hetzelfde type vergelijking hebben uitgedrukt. Dan passeren we de rechte lijn
![]()
van de algemene (of impliciete) vergelijking tot parametervergelijkingen:
![Rendered by QuickLaTeX.com \displaystyle s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases} \xrightarrow{x \ = \ t} \ \begin{cases} 2t+y=0 \\[1.7ex] z=-2\end{cases} \longrightarrow \ \begin{cases} x=t \\[1.7ex] y=-2t \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8dbc805cb7e0020c9c82c90e56e011_l3.png)
De richtingsvector van elke lijn is dus:
![]()
De coördinaten van de richtingsvectoren van de twee lijnen zijn proportioneel, dus het kunnen alleen samenvallende of evenwijdige lijnen zijn. Daarom is het in dit specifieke geval niet nodig om de exacte relatieve positie te berekenen, aangezien evenwijdige lijnen en samenvallende lijnen coplanaire lijnen zijn. De twee lijnen zijn dus coplanair .