Op deze pagina vindt u hoe de afstand tussen twee lijnen in de ruimte wordt berekend (in R3), ongeacht hun type (parallel, secans, samenvallend, secans, loodrechte lijnen, enz.). Bovendien kunt u stap voor stap voorbeelden en oefeningen zien die zijn opgelost.
Hoe de afstand tussen twee lijnen te berekenen
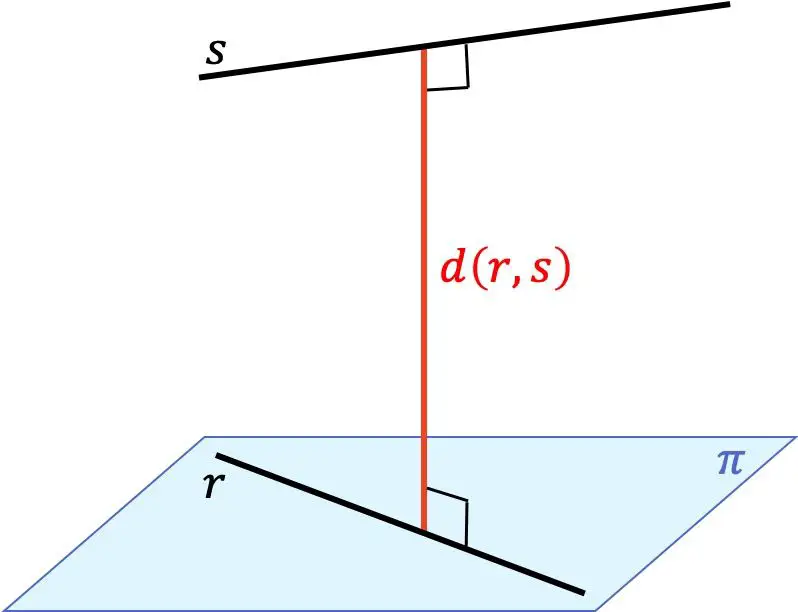
De afstand tussen twee lijnen is de minimale afstand tussen een punt op de ene lijn en een punt op de andere lijn. Deze afstand komt overeen met de lengte van het segment dat van de ene lijn naar de andere lijn gaat en dat tegelijkertijd loodrecht op beide lijnen staat.
Het vinden van de afstand tussen twee verschillende lijnen in de driedimensionale (3D) ruimte hangt dus af van de relatieve positie daartussen:
- Als de twee lijnen samenvallen of elkaar snijden , is de afstand tussen de twee lijnen nul, omdat ze elkaar (minstens) op één punt snijden.
- Als de twee lijnen evenwijdig zijn, moeten we een willekeurig punt op een van de lijnen nemen en de afstand tussen dat punt en de andere lijn berekenen (hieronder ziet u een voorbeeld van hoe u dit kunt doen).
- Als de twee lijnen elkaar in de ruimte snijden , moeten we de formule voor de afstand tussen twee snijdende lijnen toepassen (zie hieronder voor een gedetailleerde uitleg).
Om de afstand tussen twee lijnen te berekenen, moet je dus eerst weten wat voor soort lijnen het zijn en vervolgens, afhankelijk van het geval, de ene of de andere formule gebruiken. Daarom is het belangrijk dat je al beheerst hoe je de relatieve positie van twee lijnen in de ruimte kunt vinden voordat je verdergaat, maar als je je niet meer herinnert hoe het in de link is gedaan, zul je een zeer volledige uitleg zien, evenals voorbeelden en opgeloste oefeningen stap voor stap.
Hoe de afstand tussen twee parallelle lijnen in de ruimte te vinden
Het berekenen van de afstand tussen twee evenwijdige lijnen in de ruimte (in R3) gebeurt op dezelfde manier als in het vlak (in R2): je moet een punt op een van de twee lijnen nemen en de afstand van dit punt op de andere vinden lijn.
De formule voor het berekenen van de afstand van een punt tot een lijn in 3 dimensies (en die wordt gebruikt om de afstand tussen twee parallelle lijnen te bepalen) is dus:
Goud:
-
is de grootte van de richtingsvector van de lijn
-
is een punt op de lijn
een punt op de lijn
En
de vector gedefinieerd door de twee punten
-
is de grootte van het kruisproduct tussen de vectoren
En
We gaan als voorbeeld een afstandsprobleem tussen 2 evenwijdige lijnen in de ruimte oplossen:
- Wat is de afstand tussen de volgende twee parallelle lijnen?
Beide lijnen worden uitgedrukt in de vorm van een vectorvergelijking, daarom kunnen we gemakkelijk de richtingsvector en een punt van elk ervan achterhalen:
![\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91c721e906a848c6c129721fe7908112_l3.png "Rendered by QuickLaTeX.com")
Als u twijfels heeft over het bepalen van de richtingsvector en een punt van een lijn, raden wij u aan de uitleg van de vergelijking van de lijn te bekijken. Daar hebben we het voor alle vergelijkingen van de lijn uitgelegd, omdat het vinden van de richtingsvector en een punt dat bij een lijn hoort afhangt van het type vergelijking waarin de lijn wordt uitgedrukt.
Om nu de afstand tussen de twee parallelle lijnen te vinden, moeten we de formule voor de afstand van een punt tot een lijn toepassen:
Dus aan de ene kant berekenen we de module van de vector die voortkomt uit het vectorproduct. Als u twijfelt over de manier waarop dit wordt berekend, kunt u de vectorproductformule raadplegen, waar u bovendien voorbeelden en opgeloste oefeningen van deze bewerking tussen vectoren kunt zien.
![\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f166cb84d794adae8b8e5678790a5ad8_l3.png "Rendered by QuickLaTeX.com")
En aan de andere kant vinden we de grootte van de vector van de lijn
Ten slotte vervangen we de waarde van elke term in de formule en berekenen we de afstand tussen de lijnen:
Daarom is de afstand tussen de twee lijnen 3,60 eenheden.
Hoe de afstand tussen twee kruisende lijnen in de ruimte te bepalen
Zoals we in het begin zagen, verschilt de methode voor het bepalen van de afstand tussen twee kruisende lijnen van de procedure voor afstanden tussen parallelle lijnen.
Er zijn dus verschillende methoden om de afstand tussen twee kruisende lijnen in de ruimte te bepalen. Op deze pagina leggen we slechts één procedure uit, de eenvoudigste, omdat de andere twee methoden langer en ingewikkelder zijn en feitelijk praktisch niet worden gebruikt.
Laat de richtingsvector en elk punt van twee snijdende lijnen zijn:
![\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-569f8d554a0f3704d247862d0b8ef852_l3.png "Rendered by QuickLaTeX.com")
De formule voor de afstand tussen twee snijdende lijnen is:
![d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c613737cb66f811b123f886afd479e0a_l3.png "Rendered by QuickLaTeX.com")
Goud
![\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|](https://mathority.org/wp-content/ql-cache/quicklatex.com-dbc3e38427d29b2f4444ea732f955500_l3.png "Rendered by QuickLaTeX.com")
is de absolute waarde van het gemengde product van de vectoren
en de vector gedefinieerd door de punten
En
. En aan de andere kant,
is de amplitude van het kruisproduct tussen de richtingsvectoren van de twee gekruiste lijnen.
Om u te laten zien hoe u de afstand tussen twee gekruiste lijnen kunt bepalen, zullen we als voorbeeld een probleem oplossen:
- Wat is de afstand tussen de volgende twee kruisende lijnen?
Eerst moeten we de richtingsvector en een punt op elke lijn identificeren. De twee lijnen worden uitgedrukt in de vorm van een continue vergelijking, daarom:
![\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b990f78d0263975304586abbd330167_l3.png "Rendered by QuickLaTeX.com")
En nu passen we de formule toe voor de afstand tussen twee snijdende lijnen:
Enerzijds lossen we het gemengde product (of het drievoudige scalaire product) op:
![\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-c52c12945d04e320e688caf714569113_l3.png "Rendered by QuickLaTeX.com")
En aan de andere kant vinden we de module van het kruisproduct (of kruisproduct):
![\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-71afa7d4b49e542300c12b5263858665_l3.png "Rendered by QuickLaTeX.com")
Ten slotte vervangen we de waarde van elke term in de formule voor de afstand tussen twee gekruiste lijnen:
![d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0aac39997c35738e8e84a29ff7c97c6_l3.png "Rendered by QuickLaTeX.com")