Op deze pagina vind je wat loodrechte vlakken zijn, hoe je bepaalt of twee vlakken loodrecht staan, hoe je een loodrecht vlak berekent, voorbeelden en opgeloste oefeningen van loodrechte vlakken,…
Wat zijn twee loodrechte vlakken?
In de analytische meetkunde staan twee vlakken loodrecht wanneer ze elkaar onder een rechte hoek (90º) snijden.
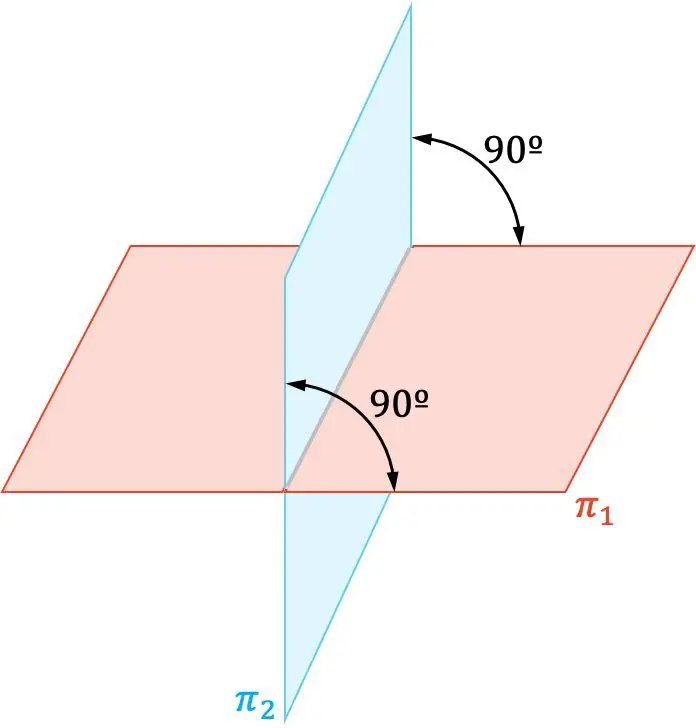
Bovendien zijn de normaalvectoren van twee loodrechte vlakken ook loodrecht op elkaar.
Het is duidelijk dat de afstand tussen twee loodrechte vlakken altijd nul is, omdat ze elkaar in een lijn snijden. Hoewel het heel eenvoudig lijkt, is het concept van de afstand tussen twee vlakken erg belangrijk, dus we raden je aan de link te bezoeken als je er vragen over hebt.
Aan de andere kant zijn twee loodrecht gepositioneerde vlakken niet de enige mogelijke relatieve positie tussen vlakken, aangezien twee vlakken in de ruimte (in R3) ook elkaar kunnen snijden, evenwijdig of samenvallend.
Hoe weet je of het ene vlak loodrecht op het andere staat?
Nadat we de definitie van loodrechte vlakken hebben gezien, gaan we kijken hoe we kunnen weten of twee vlakken loodrecht staan of niet:
Twee vlakken staan loodrecht als hun normaalvectoren loodrecht staan. Om te bepalen of twee vlakken loodrecht op elkaar staan, moeten we daarom de hoek berekenen die wordt gevormd door hun normaalvectoren, en als deze een hoek van 90 graden vormen, betekent dit dat de vlakken loodrecht staan.
Om de loodrechtheid van twee vlakken te vinden, moet je dus weten hoe je de hoek tussen twee vectoren berekent . Als u niet meer weet hoe u dit moet doen, kunt u de link raadplegen, waar u onze uitleg vindt, evenals de benodigde formule om de hoek tussen twee vectoren te bepalen. Daarnaast krijg je voorbeelden te zien en te oefenen met opgeloste oefeningen.
Maar kort gezegd staan twee vectoren loodrecht als hun puntproduct nul is. Daarom zullen twee vlakken loodrecht staan als het puntproduct van de bijbehorende normaalvectoren 0 is.
Voorbeeld van twee loodrechte vlakken
Laten we bijvoorbeeld controleren of de volgende twee vlakken loodrecht staan:
![]()
![]()
De coördinaten X, Y, Z van de vector loodrecht op een vlak vallen samen met de coëfficiënten A, B, C van de algemene (of impliciete) vergelijking ervan. Daarom is de normaalvector voor elk vlak:
![]()
![]()
En nu controleren we of dit twee loodrechte vlakken zijn door het puntproduct tussen hun normaalvectoren te berekenen:
![Rendered by QuickLaTeX.com \begin{aligned} \vv{n}_1 \cdot \vv{n}_2 & = (3,-4,2)\cdot (2,5,7) \\[2ex] & = 3 \cdot 2 +(-4) \cdot 5 +2 \cdot 7 \\[2ex] &=6-20+14 \\[2ex] &\bm{= 0}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94cfcef6a93720224eff0bd4891839ed_l3.png)
Het puntproduct tussen de twee normaalvectoren is 0, dus de twee vlakken staan loodrecht op elkaar.
Bereken een vlak loodrecht op een lijn in een punt
Een typisch vlakken- en lijnenprobleem is het vinden van de vergelijking van een vlak loodrecht op een lijn in een bepaald punt. Vervolgens zullen we zien hoe het wordt opgelost aan de hand van een voorbeeld:
- Zoek de vergelijking van het vlak loodrecht op de lijn.

Over
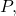
recht gezegd en punt:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=-1+4t \\[1.7ex] z=1+t \end{cases} \qquad \qquad P(1,3,-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ac7260ee9792daec4f32e1f200df01b_l3.png)
Eerst moeten we de vector loodrecht op het betreffende vlak vinden. en zoals de rechte lijn
![]()
loodrecht op het vlak staat, zal de normaalvector ervan samenvallen met de richtingsvector van de lijn.
In dit geval de lijn
![]()
heeft de vorm van parametervergelijkingen, dus de componenten van de richtingsvector zijn de termen vóór de parameter
![]()
![]()
De vector loodrecht op het vlak zal dus dezelfde zijn als de richtingsvector van de lijn:
![]()
En daarom zal de impliciete (of algemene) vergelijking van het plan de volgende zijn:
![]()
Het is daarom voldoende om de waarde van de coëfficiënt D te bepalen. Om dit te doen, vervangen we de coördinaten van het punt waarvan de verklaring ons vertelt dat het tot het vlak behoort in de vergelijking:
![]()
![]()
![]()
![]()
![]()
Kort gezegd is de cartesiaanse vergelijking van het vlak:
![]()
Als je daarentegen meer oefeningen wilt oefenen over de loodrechtheid tussen geometrische objecten, kun je onze pagina over loodrechte lijnen bezoeken. Je vindt er alles wat je moet weten over loodrechte lijnen : wanneer twee lijnen loodrecht staan, hoe je de ene loodrecht op de andere kunt berekenen, voorbeelden, opgeloste oefeningen en nog veel meer.
Eigenschappen van loodrechte vlakken
Alle loodrechte vlakken hebben de volgende kenmerken:
- Symmetrische relatie : Als een vlak loodrecht staat op een ander vlak, staat dit vlak ook loodrecht op het eerste vlak. Deze eigenschap wordt ook vastgehouden door parallelle vlakken.
![]()
- Niet-reflexieve eigenschap : Het is duidelijk dat geen enkel vlak loodrecht op zichzelf kan staan.
![]()
- Stelling: In de driedimensionale (3D) ruimte moet elk paar vlakken loodrecht op een derde vlak noodzakelijkerwijs evenwijdig zijn. Met andere woorden, als een vlak loodrecht staat op een ander vlak en dit vlak staat ook loodrecht op een derde vlak, dan zijn het eerste en het laatste vlak evenwijdig aan elkaar.