Afstand van een punt tot een vlak in de ruimte (formule)

Op deze pagina vind je hoe de afstand tussen een punt en een vlak in de ruimte wordt berekend (formule). Daarnaast kun je voorbeelden zien en oefenen met oefeningen die stap voor stap worden opgelost.

Wat is de afstand van een punt tot een vlak?

In de analytische meetkunde is de afstand van een punt tot een vlak de kortste afstand tussen het punt en een ander punt in het vlak. Deze afstand komt overeen met de lengte van het segment loodrecht op het vlak dat van het punt naar het vlak gaat.

Formule voor de afstand van een punt tot een vlak

Als we eenmaal precies het begrip afstand tussen een punt en een vlak hebben gezien, laten we nu de formule bekijken om die afstand te berekenen:

Gegeven een punt en de algemene (of impliciete) vergelijking van een vlak:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

De formule voor de afstand van een punt tot een vlak is:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Het bewijs van de formule voor de afstand van een punt tot een vlak is behoorlijk vervelend en lang, dus dat zullen we op deze pagina niet doen.

Aan de andere kant, als we bij het toepassen van de formule een resultaat verkrijgen dat gelijk is aan nul, betekent dit uiteraard dat de afstand tussen het punt en het vlak nul is en dat het punt daarom deel uitmaakt van dat vlak.

Merk ten slotte op dat om de formule toe te passen, het plan moet worden gedefinieerd als een algemene (of impliciete) vergelijking. Dus als het zou worden uitgedrukt door een ander type vlakvergelijking, zouden we het eerst in een algemene vergelijking moeten omzetten en dan de formule moeten gebruiken.

Voorbeeld van het berekenen van de afstand van een punt tot een vlak

Zodat je kunt zien hoe de afstand tussen een punt en een vlak numeriek wordt bepaald, lossen we hieronder een voorbeeld op:

Bereken de afstand tussen punt P en vlak π. Dat gezegd hebbende, punt en plan:

$P(1,3,-2) \qquad \qquad \pi: \ 2x+5y-4z+7=0$

Om de afstand van het punt tot het vlak te vinden, past u eenvoudigweg de formule toe die u in het bovenstaande gedeelte ziet:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

Nu vervangen we de waarde van elke onbekende in de formule:

$d(P,\pi) = \cfrac{\lvert 2\cdot 1+5\cdot 3-4\cdot (-2)+7\rvert}{\sqrt{2^2+5^2+(-4)^2}}$

En ten slotte voeren we de bewerkingen uit:

$d(P,\pi) = \cfrac{\lvert 2+15+8+7\rvert}{\sqrt{4+25+16}}$

$\bm{d(P,\pi) = }\cfrac{\bm{32}}{\bm{\sqrt{45}}}$

Merk op dat er in de teller van de breuk een absolute waarde staat en in de noemer een vierkantswortel, dus het resultaat moet altijd positief zijn. Dit is logisch omdat afstanden niet negatief kunnen zijn, maar altijd positief.

Bereken de afstand tussen twee evenwijdige vlakken

Twee parallelle vlakken bevinden zich altijd op dezelfde afstand. Om de afstand tussen twee parallelle vlakken te vinden, kunnen we daarom een punt op een van de twee vlakken nemen en de afstand vanaf dat punt tot het andere vlak berekenen.

Het is een methode om de afstand tussen twee parallelle vlakken te vinden. Er is echter een nog eenvoudiger manier om dit te doen wanneer de coëfficiënten A, B en C van de vergelijkingen van de twee vlakken samenvallen:

Beschouw de algemene (of impliciete) vergelijkingen van twee parallelle vlakken:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

De formule voor het berekenen van de afstand tussen twee evenwijdige vlakken is:

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

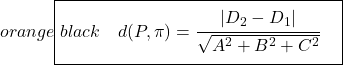
Het is dus zeker gemakkelijker om de afstand tussen twee parallelle vlakken te vinden met behulp van de formule, omdat het gewoon een kwestie is van het toepassen van de formule en dat is alles, maar het hangt af van het probleem. Bovendien denken we dat het het beste is om beide manieren om afstand te berekenen uit te leggen, zodat u degene kunt kiezen die u verkiest.

Voorbeeld van het berekenen van de afstand tussen twee evenwijdige vlakken

Als voorbeeld berekenen we de afstand tussen de volgende twee vlakken:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

We moeten eerst verifiëren dat we te maken hebben met twee evenwijdige vlakken. Alle coëfficiënten van de vlakvergelijkingen zijn dus proportioneel, behalve de onafhankelijke termen, dus het zijn in feite twee parallelle vlakken.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In dit geval vallen de termen A, B en C van de vergelijkingen van de twee vlakken niet samen, maar we kunnen dit bereiken door de gehele vergelijking van het tweede vlak door twee te delen:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

De vergelijkingen van de twee vlakken hebben dus al dezelfde coëfficiënten A, B en C. Daarom kunnen we eenvoudig de afstand tussen de twee vlakken berekenen met de formule voor de afstand tussen twee evenwijdige vlakken:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

We vervangen de waarden en lossen de bewerkingen op:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Zodat de afstand tussen het ene vlak en het andere vlak gelijk is aan één.

Afstandsproblemen van een punt tot een vlak oplossen

Oefening 1

Bereken de afstand tussen het punt P en het vlak waarvan de cartesiaanse (of algemene) vergelijking luidt:

$P(2,0,-1) \qquad \qquad \pi: \ x-3y+2z-4=0$

zie oplossing

Om de afstand van het punt tot het vlak te berekenen, moet u de bijbehorende formule gebruiken:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

We vervangen de waarde van elke parameter in de formule:

$d(P,\pi) = \cfrac{\lvert 1\cdot 2+(-3)\cdot 0+2\cdot (-1)-4\rvert}{\sqrt{1^2+(-3)^2+2^2}}$

En ten slotte voeren we de bewerkingen uit:

$d(P,\pi) = \cfrac{\lvert 2+0-2-4\rvert}{\sqrt{1+9+4}}$

$d(P,\pi) = \cfrac{\lvert -4\rvert}{\sqrt{14}}$

$\bm{d(P,\pi) = }\cfrac{\bm{4}}{\bm{\sqrt{14}}}$

Oefening 2

Bereken de afstand tussen punt P en vlak π:

$P(-1,4,3) \qquad \qquad \pi: \ y=5x-2z$

zie oplossing

Voordat we de formule voor de afstand van een punt tot een vlak gebruiken, moeten we eerst het vlak uitdrukken in de vorm van een impliciete (of algemene) vergelijking:

$\pi: \ -5x+y+2z=0$

En nu kunnen we de formule gebruiken om de afstand van het punt tot het vlak te bepalen:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

We vervangen de waarde van elke term in de formule:

$d(P,\pi) = \cfrac{\lvert -5\cdot (-1)+1\cdot 4+2\cdot 3+0\rvert}{\sqrt{(-5)^2+1^2+2^2}}$

En ten slotte voeren we de bewerkingen uit:

$d(P,\pi) = \cfrac{\lvert 5+4+6\rvert}{\sqrt{25+1+4}}$

$\bm{d(P,\pi) = }\cfrac{\bm{15}}{\bm{\sqrt{30}}}$

Oefening 3

Gebruik de formule voor de afstand tussen een punt en een vlak om te bepalen of punt P in het vlak π ligt.

$P(0,-3,5) \qquad \qquad \pi: \ 4x+6y+2z+8=0$

zie oplossing

Om te controleren of het punt tot het vlak behoort, kunnen we de afstand tussen de twee berekenen: als de afstand nul is, betekent dit dat het punt wel tot het vlak behoort, maar als de afstand anders is dan 0 betekent dit dat de punt ligt buiten het vlak. plan.

Daarom bepalen we de afstand tussen het punt en het vlak aan de hand van de formule:

$d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}}$

$d(P,\pi) = \cfrac{\lvert 4\cdot 0+6\cdot (-3)+2\cdot 5+8\rvert}{\sqrt{4^2+6^2+2^2}}$

$d(P,\pi) = \cfrac{\lvert -18+10+8\rvert}{\sqrt{16+36+4}}$

$d(P,\pi) = \cfrac{0}{\sqrt{56}}$

$\bm{d(P,\pi) = 0}$

De afstand tussen het punt en het vlak is gelijk aan nul, dus feitelijk behoort het punt tot het vlak.

Oefening 4

Bereken de afstand tussen de volgende twee vlakken:

$\pi_1 : \ 2x-y+5z-3=0 \qquad \qquad \pi_2 : \ 2x-y+5z-7=0$

zie oplossing

We moeten eerst verifiëren dat we te maken hebben met twee evenwijdige vlakken. Alle coëfficiënten van de vergelijkingen van de twee vlakken zijn proportioneel, met uitzondering van de onafhankelijke termen, dus dit zijn inderdaad twee parallelle vlakken.

$\cfrac{2}{2}=\cfrac{-1}{-1}=\cfrac{5}{5} \neq \cfrac{-3}{-7} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

In dit geval berekenen we de afstand tussen de twee vlakken met de formule, aangezien hun coëfficiënten A, B en C gelijk zijn:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

We vervangen dus de waarden in de formule en voeren de bewerkingen uit:

$d(P,\pi) = \cfrac{\lvert -7-3\rvert}{\sqrt{2^2+(-1)^2+5^2}}= \cfrac{\lvert -10\rvert}{\sqrt{30}} = \cfrac{\bm{10}}{\bm{\sqrt{30}}}$

Oefening 5

Bereken de afstand tussen de volgende twee evenwijdige vlakken:

$\pi_1 : \ \begin{cases} x=3+4\lambda-2 \mu \\[1.7ex]y=-2+\lambda+6 \mu \\[1.7ex]z=5-\lambda+3 \mu \end{cases}\qquad \qquad \pi_2 : \ 3x+2y-2z-9=0$

zie oplossing

Het voorgrondvlak wordt gedefinieerd in de vorm van parametrische vergelijkingen, dus om de formule voor de afstand tussen twee parallelle vlakken toe te passen moeten we deze eerst omzetten in de vorm van een algemene vergelijking en dat kost veel berekeningen en tijd. Daarom is het sneller als we een punt op dat vlak nemen en de afstand vanaf dat punt tot het andere vlak berekenen.

De coördinaten van een punt waar het vlak π ₁ doorheen gaat, komen dus overeen met de onafhankelijke termen van elke parametervergelijking:

$P(3,-2,5)$