Punt symmetrisch ten opzichte van een ander punt, een lijn en een vlak

Hier leest u hoe u het symmetriepunt kunt berekenen ten opzichte van een ander punt, ten opzichte van een lijn en ten opzichte van een vlak. Bovendien kunt u stap voor stap voorbeelden en oefeningen zien die zijn opgelost.

Punt symmetrisch naar een ander punt

Voordat we kijken hoe het symmetrische punt wordt berekend, gaan we eerst bekijken wat een symmetrisch punt precies is ten opzichte van een ander punt:

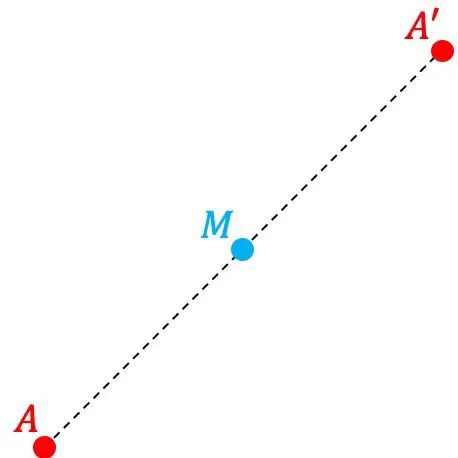
Punt A’ is het symmetrische punt van punt A ten opzichte van een ander punt M als punt A’ symmetrisch gelegen is op dezelfde afstand van punt M als de afstand tussen de punten A en M. Daarom is M het middelpunt van het segment gevormd door punten A en A’.

punt symmetrisch ten opzichte van een ander punt

$d(A,M) = d(A',M )$

Aan de andere kant zeggen we ook dat punt M het symmetriecentrum is.

Om de coördinaten van het symmetriepunt te berekenen, gebruiken we dus de formule voor het middelpunt van een lijnstuk :

$\cfrac{A+A'}{2}=M$

Uit deze vergelijking extraheren we het onbekende punt A’ en verkrijgen we de formule voor het punt dat symmetrisch is ten opzichte van een ander punt:

$\color{orange} \boxed{ \color{black} \quad A' = 2M - A \quad \vphantom{\Bigl)}}$

Voorbeeld van het vinden van het punt symmetrisch ten opzichte van een ander punt

Als voorbeeld berekenen we het symmetriepunt van punt A ten opzichte van punt M. Beschouw de twee punten:

$A(1,3,0) \qquad \qquad M(-1,4,2)$

Om het symmetriepunt tussen deze twee punten te bepalen, passen we de formule toe voor het symmetriepunt ten opzichte van een ander punt:

$A' = 2M - A$

Nu vervangen we de punten in de formule:

$A' = 2(-1,4,2) -(1,3,0)$

En wij opereren:

$A' = (-2,8,4) -(1,3,0)$

$\bm{A'=(-3,5,4)}$

punt symmetrisch ten opzichte van een rechte lijn

We hebben zojuist het idee gezien van een punt dat symmetrisch is ten opzichte van een ander punt. Welnu, het symmetrische punt van een punt ten opzichte van een lijn lijkt erg op elkaar:

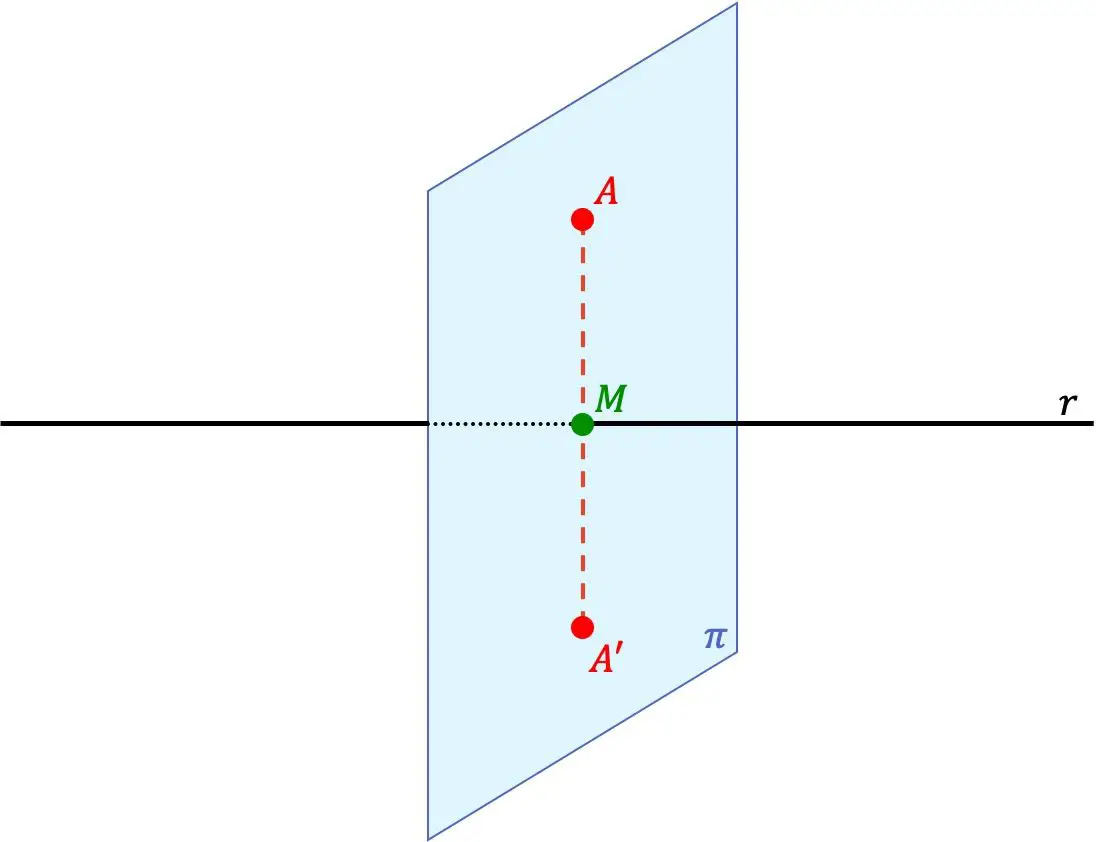
Punt A’ is het symmetrische punt van punt A ten opzichte van een lijn als de twee punten A’ en A op dezelfde lijn liggen, loodrecht op de lijn en bovendien de afstand tussen punt A’ en de lijn gelijk is aan de afstand tussen punt A en de lijn.

symmetrisch punt van een punt ten opzichte van een lijn

$d(A,r)= d(A',r)$

De lijn r is dus ook een symmetrieas tussen de punten.

Om dus het symmetriepunt van punt A ten opzichte van de lijn r te bepalen, moeten we de volgende procedure volgen:

We vinden het vlak loodrecht op de lijn r die door punt A gaat (vlak π van de vorige grafische weergave). Om dit te doen, moeten we de richtingsvector van de lijn gebruiken, die de normaalvector van het vlak zal zijn.
We berekenen het snijpunt tussen het gevonden vlak en de lijn (punt M in de vorige afbeelding).
We gebruiken de symmetrische punt-over-punt-formule (gezien in het gedeelte hierboven) om het symmetrische punt van punt A te vinden ten opzichte van punt M. Het resultaat is het symmetrische punt waar we naar op zoek waren.

Voorbeeld van het berekenen van het symmetriepunt ten opzichte van een lijn

Zodra we weten hoe we het symmetriepunt van een ander punt ten opzichte van een lijn moeten berekenen, zullen we als voorbeeld een oefening opgelost zien:

Zoek het symmetrische punt van punt A ten opzichte van de lijn r. Punt en lijn gezegd:

$\displaystyle A(4,0,-1) \qquad \qquad r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases}$

Eerst moeten we het vlak berekenen dat loodrecht staat op de lijn r en dat door punt A gaat. De vector loodrecht op dit vlak is de richtingsvector van de lijn, waarvan de componenten de termen vóór de parameter zijn.

$t$

omdat het wordt uitgedrukt in de vorm van parametervergelijkingen:

$\vv{n}=(1,4,-3)$

En de coëfficiënten A, B en C van de vergelijking van een vlak vallen samen met de coördinaten van zijn normaalvector, dus:

$\vv{n}=(1,4,-3) \quad \longrightarrow \quad \pi : \ 1x+4y-3z+D=0$

Punt A moet op dit vlak liggen, dus we kunnen nu punt A in de vergelijking van het vlak vervangen om de coëfficiënt D te vinden:

$A(4,0,-1)$

$4+4\cdot 0-3\cdot (-1)+D=0$

$4+3+D=0$

$7+D=0$

$D=-7$

De vergelijking van het vlak loodrecht op de lijn ry die door punt A gaat, is dus:

$\pi : \ x+4y-3z-7=0$

Zodra we de vergelijking van het vlak kennen, moeten we het snijpunt van het vlak en de lijn berekenen. Om dit te doen, vervangen we de coördinaten van de lijn in de vergelijking van het vlak en lossen we de resulterende vergelijking op:

$\displaystyle r: \ \begin{cases}x=1 + t \\[1.7ex] y=5 +4t\\[1.7ex] z=-4-3t \end{cases} \qquad \qquad \pi : \ x+4y-3z-7=0$

$(1+t)+4(5+4t)-3(-4-3t)-7=0$

$1+t+20+16t+12+9t-7=0$

$26t+26=0$

$26t=-26$

$t=\cfrac{-26}{26}$

$t=-1$

Nu vervangen we de waarde van

$t$

verkregen in de vergelijking van de lijn:

$\displaystyle t=-1 \ \longrightarrow \ \begin{cases}x=1 -1=0 \\[1.7ex] y=5 +4\cdot (-1)=1\\[1.7ex] z=-4-3\cdot (-1)=-1 \end{cases}$

Het snijpunt tussen de lijn r en het vlak loodrecht daarop is dus:

$M(0,1,-1)$

Tenslotte is het voldoende om het symmetrische punt van punt A te vinden ten opzichte van punt M; Hiervoor kunnen we de formule aan het begin van deze pagina gebruiken:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(0,1,-1) - (4,0,-1) \\[2ex] & = (0,2,-2)-(4,0,-1)\\[2ex] & = \bm{(-4,2,-1)} \end{aligned}$

punt symmetrisch ten opzichte van een vlak

Voordat we de methode bekijken voor het bepalen van het symmetriepunt van een ander punt ten opzichte van een vlak, laten we eens kijken wat de definitie ervan is:

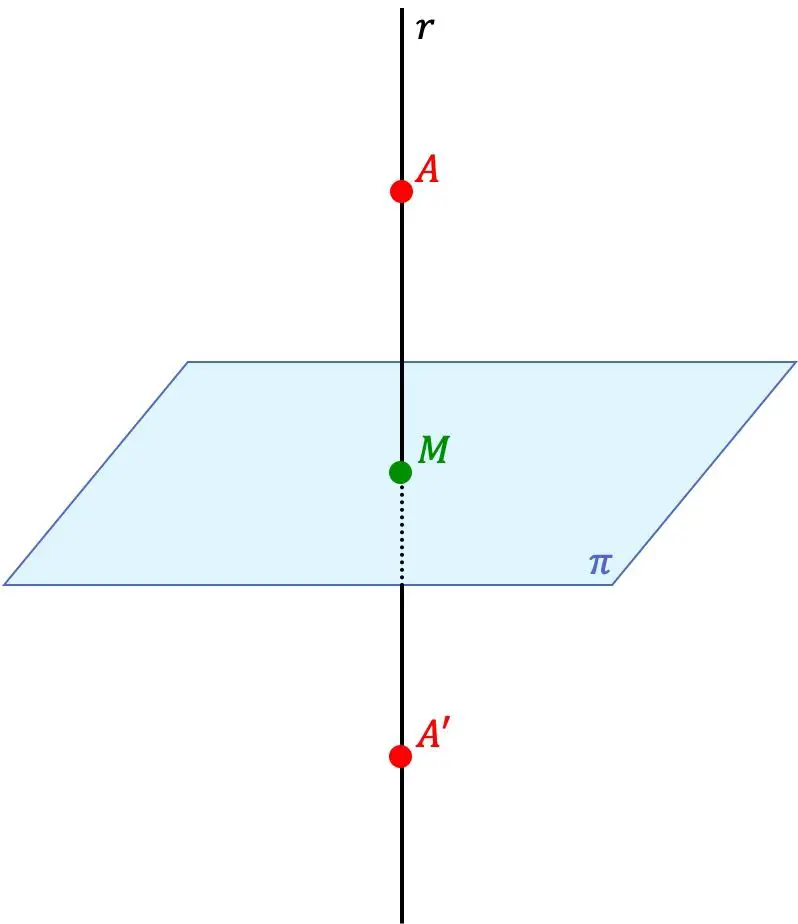
Punt A’ is het symmetrische punt van punt A ten opzichte van een vlak als de twee punten A’ en A op dezelfde lijn loodrecht op het vlak liggen en bovendien de afstand tussen punt A’ en het vlak gelijk is aan de afstand tussen punt A en het vlak.

punt symmetrisch ten opzichte van een ander punt ten opzichte van een vlak

$d(A,\pi)= d(A',\pi)$

Het vlak is dus ook een symmetrievlak tussen de twee punten.

Om dus de cartesische coördinaten van het symmetrische punt van punt A ten opzichte van het vlak π te kennen, moet u de volgende stappen volgen:

We vinden de vergelijking van de lijn loodrecht op het vlak dat door punt A gaat. Hiervoor gebruiken we de vector loodrecht op het vlak als richtingsvector van de lijn.
We berekenen het snijpunt tussen het vlak en de gevonden lijn (punt M van de vorige afbeelding).
We gebruiken de symmetrische punt-over-punt-formule (gezien in het begingedeelte) om het symmetrische punt van punt A te vinden ten opzichte van punt M. Het resultaat is het symmetrische punt waarnaar we op zoek waren.

Voorbeeld van het bepalen van het symmetriepunt ten opzichte van een vlak

Hieronder zie je een opgelost probleem met betrekking tot het symmetriepunt van een ander punt ten opzichte van een vlak:

Bepaal het symmetriepunt van A ten opzichte van het vlak π. Dat gezegd hebbende, punt en plan:

$\displaystyle A(3,-4,2) \qquad \qquad \pi: \ 2x+y-z-6=0$

Het eerste dat we moeten doen is de vergelijking vinden van de lijn die loodrecht op het vlak staat en die door punt A gaat. Om dit te doen, kunnen we de vector loodrecht op het vlak gebruiken als de richtingsvector van de lijn, waarvan de componenten X, Y, Z zijn de coëfficiënten van respectievelijk de termen A, B en C van de vergelijking van het vlak:

$\pi: \ 2x+y-z-6=0 \quad \longrightarrow \quad \vv{n} = (2,1,-1)$

We kunnen nu de parametervergelijkingen construeren van de lijn loodrecht op het vlak met de gevonden richtingsvector en een van zijn punten (punt A):

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases}$

Zodra we de loodrechte lijn kennen, berekenen we het snijpunt van het vlak en de lijn door de coördinaten van de lijn in de vergelijking van het vlak te vervangen:

$\displaystyle r: \ \begin{cases}x=3 + 2t \\[1.7ex] y=-4 +t\\[1.7ex] z=2-t \end{cases} \qquad \qquad \pi : \ 2x+y-z-6=0$

$2(3+2t)+(-4+t)-(2-t)-6=0$

$6+4t-4+t-2+t-6=0$

$6t-6=0$

$6t=6$

$t=\cfrac{6}{6}$

$t=1$

Nu vervangen we de waarde van

$t$

verkregen in de vergelijking van de lijn:

$\displaystyle t=1 \ \longrightarrow \ \begin{cases}x=3 + 2\cdot 1 =5\\[1.7ex] y=-4 +1=-3\\[1.7ex] z=2-1=1 \end{cases}$

Het snijpunt tussen het vlak en de loodlijn is dus:

$M(5,-3,1)$

Ten slotte hoeven we alleen maar het symmetrische punt van punt A te vinden ten opzichte van punt M. En om dit te doen, kunnen we de formule aan het begin van deze pagina gebruiken:

$\begin{aligned} A' & = 2M - A \\[2ex] &= 2(5,-3,1) - (3,-4,2) \\[2ex] & = (10,-6,2)-(3,-4,2)\\[2ex] & = \bm{(7,-2,0)} \end{aligned}$