Parametrische vergelijkingen van het vlak

Op deze pagina vindt u wat de parametervergelijkingen van een plan zijn en hoe deze worden berekend (formule). Daarnaast kun je voorbeelden zien en oefenen met oefeningen die stap voor stap worden opgelost.

Wat zijn de parametervergelijkingen van een vlak?

In de analytische meetkunde zijn de parametervergelijkingen van een vlak vergelijkingen waarmee elk vlak wiskundig kan worden uitgedrukt. Om de parametervergelijkingen van een vlak te vinden, hebben we alleen een punt en twee lineair onafhankelijke vectoren nodig die bij dat vlak horen.

Formulering van parametervergelijkingen van het plan

Beschouw een punt en twee richtingsvectoren van een vlak:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

De formule voor de parametervergelijkingen van een vlak is:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Goud

$\lambda$

$\mu$

zijn twee scalairen, dat wil zeggen twee reële getallen.

Het is belangrijk dat de twee richtingsvectoren van de vlakvergelijking lineair onafhankelijk zijn, dat wil zeggen dat ze een verschillende (niet-parallelle) richting hebben. Anders zou de bovenstaande vergelijking geen plan vertegenwoordigen.

Houd er aan de andere kant rekening mee dat er naast de parametervergelijking ook andere manieren zijn om een vlak in de ruimte analytisch uit te drukken (in R3), zoals de algemene vlakvergelijking . In deze link vindt u de formule, hoe deze wordt berekend op basis van de parametervergelijkingen van het plan, voorbeelden en opgeloste oefeningen.

Voorbeeld van het vinden van parametervergelijkingen van een vlak

Als we eenmaal hebben gezien wat de parametervergelijking van het vlak is, gaan we kijken hoe deze wordt berekend aan de hand van een voorbeeld:

Zoek de parametervergelijkingen van het vlak dat door het punt gaat
$P(1,3,2)$

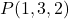
en bevat de vectoren

$\vv{\text{u}}=(2,0,-1)$

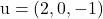
En

$\vv{\text{v}}=(4,2,3)$

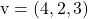
Om de parametervergelijkingen van het plan te bepalen, past u eenvoudigweg de formule toe:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

En nu vervangen we het punt en elke richtingsvector in de vergelijking:

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

Hoe je van de vectorvergelijking van een vlak naar parametervergelijkingen gaat

Een andere methode om de parametervergelijkingen van een vlak te bepalen is aan de hand van de vectorvergelijking van een vlak. Hieronder zie je de demo.

Laat de vectorvergelijking van elk vlak zijn:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

We bedienen en voeren eerst de producten van vectoren uit via de scalairen:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

Vervolgens voegen we de componenten toe:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

En ten slotte verkrijgen we de parametrische vergelijking van het vlak door de coördinaten te assimileren die overeenkomen met elke variabele afzonderlijk:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Zoals je in de twee bovenstaande voorbeelden kunt zien, is het vinden van de parametervergelijkingen van een vlak relatief eenvoudig. De problemen kunnen echter een beetje ingewikkeld worden, dus hieronder vindt u verschillende opgeloste oefeningen met verschillende moeilijkheidsgraden, zodat u kunt oefenen.

Opgeloste problemen van parametervergelijkingen van het vlak

Oefening 1

Bepaal de parametervergelijkingen van het vlak dat de vector bevat

$\vv{\text{u}}=(2,1,5)$

en doorloopt de volgende twee punten:

$A(3,2,-1)$

$B(-2,-1,1).$

zie oplossing

Om de vergelijking van een vlak te kennen, heb je een punt en twee vectoren nodig en in dit geval hebben we maar één vector, we moeten daarom een andere richtende vector van het vlak vinden. Om dit te doen, kunnen we de vector berekenen die de twee punten van het vlak definieert:

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

Nu we al twee richtingsvectoren van het vlak en een punt kennen, gebruiken we daarom de formule voor de parametervergelijkingen van het vlak:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

En we vervangen de twee vectoren en een van de twee punten op het vlak in de vergelijking:

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

Oefening 2

Zoek de parametervergelijkingen van het vlak dat de volgende drie punten bevat:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

zie oplossing

Om de parametervergelijkingen van het vlak te vinden, moeten we twee lineair onafhankelijke vectoren vinden die in het vlak met elkaar verbonden zijn. En hiervoor kunnen we twee vectoren berekenen die worden gedefinieerd door de 3 punten:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

De coördinaten van de twee gevonden vectoren zijn niet proportioneel, dus lineair onafhankelijk van elkaar.

Nu we al twee richtingsvectoren en een punt op het vlak kennen, passen we de formule toe voor de parametervergelijking van het vlak:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

En we vervangen de twee vectoren en een van de drie punten van het vlak in de vergelijking:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Oefening 3

Bereken de parametervergelijkingen van het vlak gedefinieerd door de volgende vectorvergelijking:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

zie oplossing

Om de vectorvergelijking van het vlak om te zetten in een parametrische vergelijking, moet je met de coördinaten werken en vervolgens elke variabele afzonderlijk oplossen:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

Oefening 4

Zoek de parametervergelijkingen van het vlak dat de lijn bevat

$r$

en is evenwijdig aan de rechterkant

$s.$

zijnde de lijnen:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

zie oplossing

Om de parametervergelijkingen van het vlak te vinden, moeten we twee richtingsvectoren en een punt op het vlak kennen. De instructie vertelt ons dat deze de regel bevat

$r$

Daarom kunnen we de richtingsvector en een punt op deze lijn nemen om het vlak te definiëren. Bovendien vertelt de verklaring ons dat het vlak evenwijdig is aan de lijn

$s,$

dus we kunnen de richtingsvector van deze lijn ook gebruiken voor de vlakvergelijking.

het recht

$r$

wordt uitgedrukt in de vorm van parametervergelijkingen, dus de componenten van de richtingsvector zijn de coëfficiënten van de parametertermen

$t:$

$\vv{r} =(1,-3,2)$

En de cartesiaanse coördinaten van een punt op dezelfde lijn zijn de onafhankelijke termen van de parametervergelijkingen:

$P(1,2,4)$

Aan de andere kant, de rechte lijn

$s$

heeft de vorm van een continue vergelijking, zodat de componenten van zijn richtingsvector de noemers zijn van de breuken:

$\vv{s} =(2,2,-3)$

Daarom zijn de parametervergelijkingen van het plan:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Wat zijn de parametervergelijkingen van een vlak?

Formulering van parametervergelijkingen van het plan

Voorbeeld van het vinden van parametervergelijkingen van een vlak

Hoe je van de vectorvergelijking van een vlak naar parametervergelijkingen gaat

Opgeloste problemen van parametervergelijkingen van het vlak

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren