Op deze pagina worden de verschillende relatieve posities uitgelegd die bestaan tussen een lijn en een cirkel. Bovendien kunt u zien hoe u de relatieve positie tussen een lijn en een cirkel kunt vinden.
Wat zijn de relatieve posities van een lijn en een cirkel?
In de analytische meetkunde kan de relatieve positie van een lijn ten opzichte van een cirkel alleen uitwendig, rakend of secans zijn:
- Buitenkant : wanneer de afstand tussen de lijn en het middelpunt van de cirkel groter is dan de straal.
- Raaklijn : wanneer de afstand tussen de lijn en het middelpunt van de cirkel gelijk is aan de straal.
- Secans : wanneer de afstand tussen de lijn en het middelpunt van de cirkel kleiner is dan de straal.
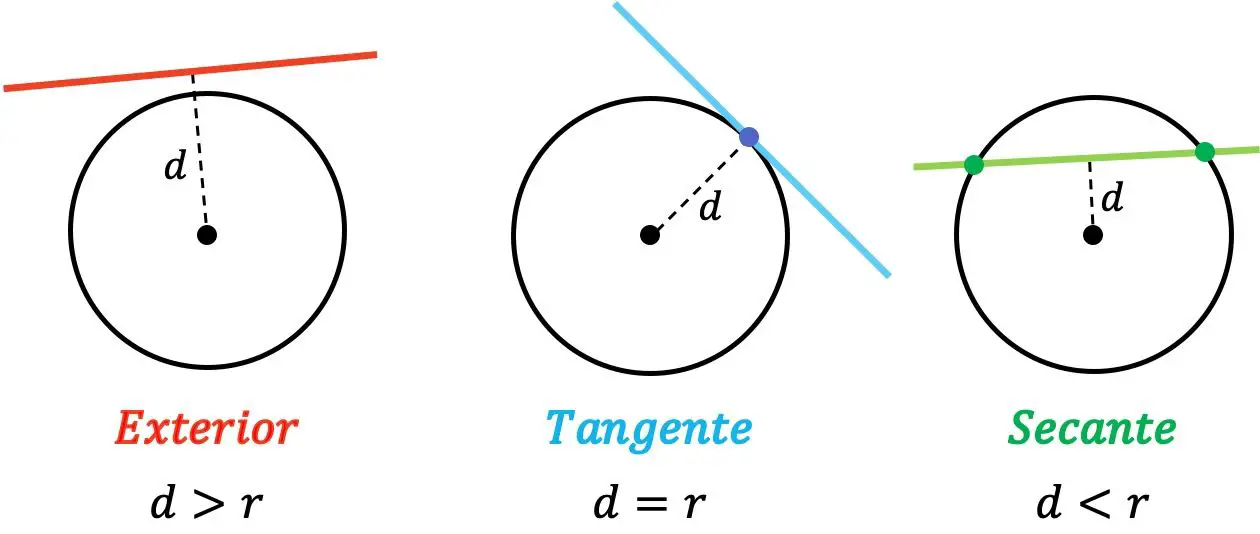
Dus als een lijn buiten een cirkel ligt, snijdt deze deze op geen enkel punt. Aan de andere kant, wanneer de lijn de cirkel raakt, hebben de twee een punt gemeenschappelijk. En ten slotte is een lijn secans op een cirkel wanneer deze deze op twee verschillende punten snijdt.
Hoe bepaal je de relatieve positie tussen een lijn en een cirkel?
Er zijn twee manieren om de relatieve positie van een lijn ten opzichte van een cirkel in het vlak te vinden: één door de afstand tussen de lijn en het middelpunt van de cirkel te berekenen, en de andere door een samengesteld stelsel van vergelijkingen op te lossen van de vergelijking van de lijn en de vergelijking van de cirkel.
Vervolgens zullen we precies zien wat elke methode is.
Methode 1: Afstand tussen de lijn en het middelpunt van de cirkel
Zoals we zagen bij de uitleg van het concept van relatieve positie tussen een lijn en een cirkel, geeft de afstand tussen een lijn en het middelpunt van een cirkel aan wat voor soort relatieve positie het is.
Deze methode bestaat dus uit het vinden van de afstand tussen de lijn en het middelpunt van de cirkel. Om dit te kunnen doen, moet je uiteraard weten hoe je de afstand tussen een punt en een lijn berekent . Op deze pagina kun je zien hoe je dat moet doen, evenals voorbeelden en opgeloste oefeningen om te oefenen.
Dus, afhankelijk van het resultaat van de verkregen afstand, zal het een of ander geval zijn:
- De lijn ligt buiten de cirkel als de verkregen afstand groter is dan de straal van de cirkel.
- De lijn raakt de cirkel als de verkregen afstand gelijk is aan de straal van de cirkel.
- De lijn zal de cirkel snijden als de verkregen afstand kleiner is dan de straal van de cirkel.
Methode 2: een stelsel vergelijkingen oplossen
Een andere manier om de relatieve positie van een lijn ten opzichte van een cirkel te vinden, is door een systeem van vergelijkingen te gebruiken dat wordt gevormd door de vergelijking van de lijn en de vergelijking van de cirkel. Om deze methode toe te passen, moet je uiteraard weten wat de vergelijking van de omtrek is en wat de formule voor de vergelijking van de lijn is.
Afhankelijk van het aantal oplossingen van het stelsel vergelijkingen, zullen we met het ene of het andere geval worden geconfronteerd:
- Als het stelsel vergelijkingen geen oplossing heeft, betekent dit dat de lijn en de cirkel geen gemeenschappelijk punt hebben, dus ligt de lijn buiten de cirkel.
- Als het stelsel vergelijkingen 1 oplossing heeft, betekent dit dat de lijn en de cirkel een gemeenschappelijk punt hebben, dus de lijn raakt de cirkel.
- Als het stelsel vergelijkingen twee oplossingen heeft, betekent dit dat de lijn en de cirkel twee punten gemeenschappelijk hebben, dus de lijn is secans ten opzichte van de cirkel.