Omtrekvergelijking -

Op deze pagina vind je alles over de vergelijking van de omtrek: gewone vergelijking, algemene vergelijking, andere soorten vergelijkingen van de omtrek, wanneer de vergelijking van een omtrek correct is,… Daarnaast zie je voorbeelden van hoe je de vergelijking vindt van een omtrek en je kunt oefenen met opgeloste oefeningen.

Gewone vergelijking van de cirkel

Laten we, voordat we kijken wat de omtrekvergelijking is, eerst het begrip omtrek in herinnering brengen:

De omtrek is de verzameling punten op het vlak die op gelijke afstand liggen van een vast punt dat het middelpunt wordt genoemd.

Daarom bevinden alle punten op een cirkel zich op dezelfde afstand van het middelpunt.

Bovendien is de cirkel een van de vier kegelsneden, samen met de ellips, parabool en hyperbool. Dat wil zeggen, een cirkel kan worden verkregen door een kegel af te snijden met een vlak evenwijdig aan de basis.

De eenvoudigste manier om een cirkel in het cartesiaanse vlak te beschrijven is aan de hand van de gewone vergelijking. De formule voor de gewone omtrekvergelijking is dus als volgt:

De gewone vergelijking van de cirkel is:

$(x-a)^2+(y-b)^2=r^2$

Goud:

$r$

is de straal van de cirkel.
$a$

En

$b$

zijn de coördinaten van het middelpunt van de cirkel:

$C(a,b)$

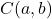
Hoewel we het niet zullen demonstreren omdat het een beetje vervelend is, kan deze vergelijking worden verkregen uit de stelling van Pythagoras.

Laten we eens kijken hoe de gewone vergelijking van een cirkel wordt berekend met een voorbeeld:

Bepaal de gewone vergelijking van de cirkel met straal 5 waarvan het middelpunt het punt is
$C(3,-1).$

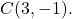
De formule voor de gewone vergelijking van een cirkel is:

$(x-a)^2+(y-b)^2=r^2$

Daarom hoeven we alleen het onbekende te vervangen

$r$

door de waarde van de straal en de onbekenden

$a$

$b$

door respectievelijk de coördinaten X en Y van het middelpunt van de cirkel:

$(x-3)^2+(y-(-1))^2=5^2$

Dus de gewone vergelijking van de cirkel is:

$\bm{(x-3)^2+(y+1)^2=25}$

Algemene vergelijking van de cirkel

Een ander type omtrekvergelijking is de algemene vergelijking; deze wordt in feite het meest gebruikt. We zullen dan zien hoe we de algemene vergelijking van elke omtrek kunnen verkrijgen uit de gewone vergelijking.

Beschouw de gewone vergelijking van een cirkel:

$(x-a)^2+(y-b)^2=r^2$

Als we de opmerkelijke gelijkheden (of opmerkelijke producten) ontwikkelen:

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

Nu maken we 3 wijzigingen in de variabelen:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

En tenslotte verkrijgen we de algemene vergelijking van de omtrek:

$x^2+y^2+Ax+By+C=0$

De formule voor de algemene vergelijking van de omtrek is daarom:

$x^2+y^2+Ax+By+C=0$

waar het middelpunt van de cirkel is:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

En de straal van de cirkel is:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

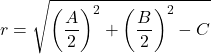
Dus deze vergelijking van de omtrek wordt altijd verkregen door de gewone vergelijking. Hier is een voorbeeld om te zien hoe het werkt:

Bepaal de algemene vergelijking van de cirkel met straal 6 waarvan het middelpunt het punt is
$C(2,4).$

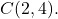
Eerst moeten we de gewone vergelijking van de cirkel vinden. Om dit te doen gebruiken we zijn formule:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

En nu werken we totdat we de algemene vergelijking van de omtrek vinden, dat wil zeggen totdat we niet langer kunnen vereenvoudigen:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

De algemene vergelijking van de cirkel is dus:

$\bm{x^2+y^2-4x-8y-16=0}$

Hoewel dit voor het probleem niet nodig was, kunnen we nu het middelpunt en de straal van de gevonden vergelijking berekenen om te verifiëren dat deze correct is.

Om het middelpunt van de cirkel te bepalen, gebruiken we de formule:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

In feite valt het middelpunt van de cirkel samen met dat van de verklaring.

We controleren ook de straal van de omtrek met de formule:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

En de straal is ook gelijk aan die van de stelling. Daarom is de berekende omtrekvergelijking correct.

Het bestaan van een omtrek

Alle vergelijkingen in de vorm van

$x^2+y^2+Ax+By+C=0$

corresponderen met een cirkel. Om dit type uitdrukking echt de vergelijking van een cirkel te laten zijn, moet dus aan de volgende drie voorwaarden worden voldaan:

De coëfficiënten van
$x^2$

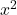
en van

$y^2$

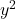
ze moeten gelijk zijn aan 1. Houd er rekening mee dat als beide variabelen werden voorafgegaan door een ander getal dan één, maar ze allebei hetzelfde getal hadden, de hele vergelijking door dat getal kon worden gedeeld, zodat hun coëfficiënten 1 zijn.
De vergelijking kan geen term hebben
$xy.$
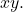
De volgende uitdrukking moet positief zijn:

De twee cirkelvergelijkingen die we hebben gezien, de gewone vergelijking en de algemene vergelijking, worden het meest gebruikt om een cirkel in het vlak wiskundig uit te drukken (in R2). Er zijn echter verschillende soorten vergelijkingen om dit geometrische object te beschrijven. Hieronder vindt u de uitleg van elk ervan.

Canonieke vergelijking van de cirkel

De canonieke vergelijking, of gereduceerde vergelijking, van een cirkel wordt gebruikt om elke cirkel te beschrijven waarvan het middelpunt zich in de oorsprong van de coördinaten bevindt , dat wil zeggen in het punt (0,0). Genoemde vergelijking is als volgt:

$x^2+y^2=r^2$

Als bovendien de straal gelijk zou zijn aan eenheid (1), zou de vergelijking van de omtrek zijn:

$x^2+y^2=1$

Deze laatste vergelijking komt overeen met de goniometrische omtrek, ook wel eenheidsomtrek of eenheidscirkel genoemd. Het is de cirkel met straal 1, gecentreerd op de oorsprong van de coördinaten.

Vergelijkingen van twee concentrische cirkels

Twee concentrische vergelijkingen zijn vergelijkingen waarvan het middelpunt zich in hetzelfde punt bevindt. En het enige dat twee concentrische cirkels verschillend is, is de straal.

Om aan deze voorwaarde te voldoen, zijn de vergelijkingen van twee concentrische cirkels precies hetzelfde, afgezien van hun onafhankelijke termen, die verschillend moeten zijn.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

De volgende twee cirkels zijn bijvoorbeeld concentrisch, aangezien al hun coëfficiënten identiek zijn, behalve de onafhankelijke termen:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

Parametrische vergelijking van de cirkel

Net als de lijn kan ook de vergelijking van een cirkel worden geparametriseerd met de trigonometrische functies van sinus en cosinus. De parametervergelijkingen van de cirkel zijn dus:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

waar het punt

$(a,b)$

is het middelpunt van de cirkel en

$r$

Dit is jouw afdeling.

Opgeloste problemen van de vergelijking van een cirkel

Oefening 1

Bereken de algemene vergelijking van de cirkel met straal 5 waarvan het middelpunt zich in het punt bevindt

$C(-1,2).$

zie oplossing

Om de algemene vergelijking van de cirkel te vinden, moeten we eerst de gewone vergelijking vinden. Om dit te doen, gebruiken we de formule voor de gewone vergelijking van een cirkel:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

Zodra we de gewone vergelijking kennen, werken we totdat we de algemene vergelijking van de cirkel vinden:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

De algemene vergelijking van de cirkel is dus:

$\bm{x^2+y^2+2x-4y-20=0}$

Oefening 2

Zoek voor elk van de volgende cirkels de coördinaten van het middelpunt en de lengte van de straal.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

zie oplossing

omtrek A)

$(x-2)^2+(y+5)^2=36$

De omtrek wordt uitgedrukt in de vorm van een gewone vergelijking, waarvan de formule is:

$(x-a)^2+(y-b)^2=r^2$

Daarom zijn de coördinaten van het middelpunt van de cirkel:

$C(a,b)$

$\bm{C(2,-5)}$

En de straal is:

$r^2=36$

$\bm{r=6}$

omtrek B)

$x^2+y^2+8x-10y+1 = 0$

Deze omtrek wordt uitgedrukt in de vorm van een algemene vergelijking, dus om de coördinaten van het middelpunt te berekenen, moet je de volgende formule gebruiken:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

Aan de andere kant is de formule om de straal van de cirkel te vinden:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

omtrek C)

$x^2+y^2=4$

De omtrek wordt uitgedrukt in de vorm van een gewone vergelijking, waarvan de formule is:

$(x-a)^2+(y-b)^2=r^2$

Daarom zijn de coördinaten van het middelpunt van de cirkel:

$C(a,b)$

In dit geval heeft de vergelijking geen term.

$a$

geen van beide

$b,$

het is daarom gecentreerd op de oorsprong van de coördinaten:

$\bm{C(0,0)}$

En de straal is:

$r^2=4$

$\bm{r=2}$

Oefening 3

Welke van de volgende vergelijkingen is de vergelijking van een cirkel?

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

zie oplossing

Om een uitdrukking de vergelijking van een cirkel te laten zijn, moeten de volgende voorwaarden waar zijn:

1. De coëfficiënten van

$x^2$

en van

$y^2$

Ze moeten gelijk zijn aan 1.
2. De vergelijking kan geen term hebben

$xy.$

Vergelijking A)

$x^2+y^2+4x-6y-1=0$

De coëfficiënten van

$x^2$

$y^2$

zijn 1 en de vergelijking heeft geen term

$xy.$

Het volstaat daarom om de derde voorwaarde te controleren:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”216″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”146″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”49″ style=”vertical-align: -2px;”> <p class=$ 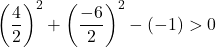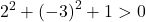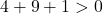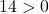De vergelijking voldoet aan de 3 voorwaarden en is dus de vergelijking van een cirkel.

Vergelijking B)

$x^2+y^2+5x+5y+2xy-4 = 0$

De vergelijking heeft een term met

$xy,$

waarbij de vergelijking niet overeenkomt met een cirkel.

Vergelijking C)

$2x^2+2y^2-8x+4y+2=0$

De coëfficiënten van

$x^2$

$y^2$

zijn niet 1, maar we kunnen de vergelijking transformeren door alle termen te delen:

$x^2+y^2-4x+2y+1=0$

Op deze manier nu de coëfficiënten van

$x^2$

$y^2$

ja, ze zijn 1 en bovendien heeft de vergelijking geen term

$xy.$

We hoeven daarom alleen de derde voorwaarde te bevestigen:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”189″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”158″ style=”vertical-align: -5px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p class=$ 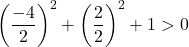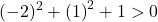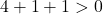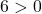De vergelijking voldoet aan de 3 voorwaarden en is dus de vergelijking van een cirkel.

Vergelijking D)

$x^2+y^2+x+2y+6=0$

De coëfficiënten van

$x^2$

$y^2$

zijn 1 en de vergelijking heeft geen term

$xy.$

Het volstaat daarom om de derde voorwaarde te controleren:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”175″ style=”vertical-align: -17px;”> 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”128″ style=”vertical-align: -4px;”> } \ 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”82″ style=”vertical-align: -4px;”> <p class=$ 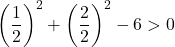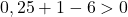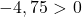De vergelijking voldoet niet aan de laatste voorwaarde en is dus niet de vergelijking van een cirkel .

Oefening 4

Bepaal de vergelijking van de cirkel die door de volgende drie punten gaat:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

zie oplossing

De algemene vergelijking van elke cirkel is:

$x^2+y^2+Ax+By+C=0$

Daarom moeten we de coördinaten van de punten in de cirkelvergelijking vervangen om de parameters te vinden

$A,$

$B$

$C.$

Met het eerste punt vinden we de coëfficiënt

$C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

Met het tweede punt vinden we de coëfficiënt

$A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

En vanaf het derde punt vinden we de coëfficiënt

$B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

Concluderend is de algemene vergelijking voor de omtrek:

$\bm{x^2+y^2-3x+y=0}$

Oefening 5

Als de tegenovergestelde uiteinden van een cirkel de volgende twee punten zijn:

$A(2,3) \qquad B(6,-1)$

Wat is de gewone vergelijking van de cirkel?

zie oplossing

Als de twee punten de uitersten van de cirkel zijn, zal het middelpunt het middelpunt tussen deze twee punten zijn:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

Aan de andere kant is de diameter van de cirkel de afstand tussen de twee punten, die kan worden berekend met behulp van de grootte van de vector die de twee punten vormen:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

En de straal van de cirkel is de helft van de diameter:

$r = \cfrac{\sqrt{32}}{2}$

De gewone vergelijking van de cirkel is daarom:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

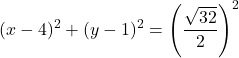
Tenslotte, als dit artikel nuttig voor u was, zult u zeker ook geïnteresseerd zijn in onze hyperbool- (wiskunde) en parabool- (wiskunde) -pagina’s. Je vindt er een gedetailleerde uitleg van wat de hyperbool en de parabool zijn, hun vergelijkingen, hun kenmerken, voorbeelden, opgeloste oefeningen…

Omtrek vergelijking

Gewone vergelijking van de cirkel

Algemene vergelijking van de cirkel

Het bestaan van een omtrek

Canonieke vergelijking van de cirkel

Vergelijkingen van twee concentrische cirkels

Parametrische vergelijking van de cirkel

Opgeloste problemen van de vergelijking van een cirkel

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren