Snijlijnen - Mathority

Op deze pagina vind je alles over secanslijnen: wat ze betekenen, de verschillende soorten die er bestaan, hoe je weet of twee lijnen secans zijn, hoe je hun gemeenschappelijk punt kunt vinden,… Je zult ook verschillende voorbeelden en opgeloste oefeningen kunnen zien van secanslijnen.

Wat zijn twee snijdende lijnen?

In de wiskunde is de definitie van snijlijnen als volgt:

Twee lijnen snijden elkaar wanneer ze elkaar slechts op één punt snijden. Daarom hebben snijdende lijnen slechts één punt gemeen. Bovendien moeten twee elkaar snijdende lijnen noodzakelijkerwijs in hetzelfde Cartesiaanse vlak liggen.

Het concept dat twee lijnen elkaar in één punt snijden is belangrijk, want als ze meer dan één snijpunt zouden hebben, zouden het samenvallende lijnen zijn en, aan de andere kant, als ze geen snijpunt zouden hebben, zouden het evenwijdige lijnen zijn.

Voorbeelden van kruisende lijnen

Nadat we de betekenis van twee elkaar kruisende lijnen hebben gezien, gaan we nu naar twee verschillende voorbeelden van dit soort lijnen kijken:

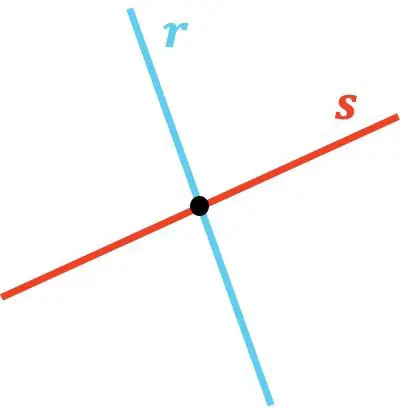
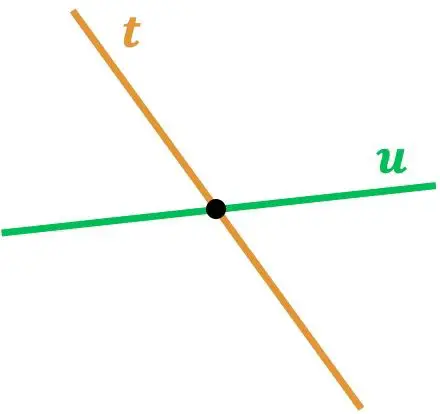
Zoals je kunt zien, snijden de lijnen r en s elkaar omdat ze elkaar op één punt raken. En op dezelfde manier snijdt lijn t lijn u , omdat er een punt is waar ze elkaar snijden.

Soorten kruisende lijnen

Er zijn twee soorten kruisende lijnen:

Loodrechte lijnen : zijn lijnen die elkaar snijden in een rechte hoek van 90°.
Schuine lijnen: bestaan uit lijnen die elkaar snijden in een scherpe hoek tussen 0º en 90º (niet inbegrepen).

Loodrechte rechte lijnen

Loodrechte lijnen zijn die lijnen die elkaar snijden en vier hoeken van 90 graden vormen.

Op dezelfde manier voldoen de hellingen van twee loodrechte lijnen altijd aan de volgende voorwaarde:

$m_r = -\cfrac{1}{m_s}$

Een andere eigenschap van loodrecht snijdende lijnen is dat het puntproduct tussen hun richtingsvectoren (een vector die de richting van een lijn aangeeft) gelijk is aan nul.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = 0$

Als je meer geïnteresseerd bent in loodrechte lijnen, kun je in deze link voorbeelden van loodrechte lijnen zien. Daarnaast zul je ook ontdekken hoe je een lijn loodrecht op een andere kunt berekenen, de eigenschappen van dit type lijn, oefeningen die stap voor stap worden opgelost, enz.

schuine lijnen

Schuine lijnen zijn die lijnen die elkaar snijden en in paren scherpe hoeken en stompe hoeken vormen. Dat wil zeggen: maak twee scherpe hoeken (kleiner dan 90°) en twee stompe hoeken (groter dan 90°). Volgens de definitie van de hoek van twee lijnen is de hoek tussen twee lijnen echter de kleinste van de hoeken die deze vormt.

De hoek tussen twee schuine lijnen met hun hellingen kan worden berekend met behulp van de volgende formule:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Hoe weet je of twee lijnen elkaar snijden?

Er zijn hoofdzakelijk 3 methoden om de relatieve positie van twee lijnen te vinden:

Met de richtingsvectoren van de twee lijnen.
Met de hellingen van de twee lijnen.
Met de impliciete (of algemene) vergelijking van de twee lijnen.

Vervolgens zullen we de uitleg zien van de 3 methoden die bestaan om te weten wanneer twee lijnen elkaar kruisen.

Van de richtingsvectoren van de lijnen

Als de coördinaten van de richtingsvectoren (vector die de richting van een lijn markeert) van twee verschillende lijnen niet proportioneel zijn , snijden deze twee lijnen elkaar.

Laten we een stap voor stap opgeloste oefening bekijken van twee kruisende lijnen:

$\displaystyle r: \ \begin{cases} x=1+2t \\[2ex] y= 5-3t \end{cases}\qquad \qquad s: \ \begin{cases} x=1+t \\[2ex] y=2+4t \end{cases}$

Beide lijnen worden uitgedrukt als parametervergelijkingen, dus de componenten van de richtingsvector van elke lijn zijn de getallen vóór de parameter

$t:$

$\vv{r} =(2,-3) \qquad \qquad \vv{s}=(1,4)$

Om te zien of de richtingsvectoren proportioneel zijn, moeten we hun coördinaten onderling verdelen. Als we in beide delingen hetzelfde resultaat verkrijgen, zijn ze proportioneel; aan de andere kant, als het resultaat anders is, betekent dit dat de vectoren niet proportioneel zijn.

$\cfrac{2}{1} \neq \cfrac{-3}{4}$

De verdelingen van de componenten zijn niet gelijkwaardig, daarom zijn de vectoren niet proportioneel en daarom snijden de lijnen elkaar.

aan het begin van de pistes

Als twee lijnen verschillende hellingen hebben, betekent dit dat de lijnen elkaar snijden.

De volgende twee lijnen snijden elkaar bijvoorbeeld omdat ze verschillende hellingen hebben:

$r: \ y=-2x+4 \qquad \qquad s: \ y=3x+1$

De helling van de lijn

$r$

is -2 en de helling van de lijn

$s$

is 3.

$m_r =-2 \neq m_s =3$

Omdat de twee lijnen niet dezelfde helling hebben, snijden ze elkaar.

Uit de impliciete vergelijking van de lijn

Via de impliciete vergelijkingen (of algemene vergelijkingen) van de lijnen kan ook worden vastgesteld of twee lijnen elkaar wel of niet snijden. De impliciete vergelijking van de lijn is als volgt:

$Ax+By+C=0$

Twee lijnen snijden elkaar dus wanneer hun coëfficiënten A en B niet proportioneel zijn.

Laten we een voorbeeld bekijken van twee elkaar kruisende lijnen gedefinieerd met hun impliciete vergelijking:

$r: \ 3x-y+5=0 \qquad \qquad s: \ -2x+6y-1=0$

Om te verifiëren dat dit twee elkaar snijdende lijnen zijn, moeten we de evenredigheid van de coëfficiënt A analyseren (het getal vóór de variabele

$x$

) met de coëfficiënt B (cijfer vóór de variabele

$y$

$\cfrac{3}{-2} \neq \cfrac{-1}{6}$

De twee termen zijn niet proportioneel, dus in feite snijden de twee lijnen elkaar.

Zoek het gemeenschappelijke punt van twee snijdende lijnen

Zoals we hebben gezien, hebben snijdende lijnen slechts één punt gemeen. Om het snijpunt van twee snijlijnen te berekenen , is het dus noodzakelijk om het stelsel vergelijkingen op te lossen dat door de twee lijnen wordt gevormd.

Als voorbeeld vinden we het snijpunt van de volgende twee lijnen:

$r: \ x+2y-5=0 \qquad \qquad s: \ 2x-3y+3=0$

Om het snijpunt van de twee lijnen te bepalen, moeten we het stelsel van lineaire vergelijkingen oplossen dat door de twee lijnen wordt gevormd:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\}$

In dit geval zullen we het systeem oplossen met de substitutiemethode. We zullen daarom de variabele isoleren

$x$

uit de eerste vergelijking en vervang deze door de tweede vergelijking:

$\left.\begin{array}{l} x+2y-5=0\\[2ex] 2x-3y+3=0\end{array}\right\} \begin{array}{l}\longrightarrow \ x=5-2y \\[2ex]&\end{array}$

$2(5-2y)-3y+3=0$

$10-4y-3y=3$

$-4y-3y=3-10$

$-7y=-7$

$y=\cfrac{-7}{-7} = 1$

En zodra we weten hoeveel het onbekende waard is

$y$

We vervangen de waarde ervan in de gevonden uitdrukking

$x:$

$x=5-2y \ \xrightarrow{y \ = \ 1} \ x=5-2\cdot 1$

$x = 5-2 = 3$

De oplossing van het stelsel vergelijkingen is daarom het snijpunt van de twee lijnen. En dit punt is

$\bm{(3,1)}.$

lijn die een cirkel snijdt

Als we zeggen dat twee lijnen elkaar kruisen, bedoelen we normaal gesproken het concept dat we zojuist hebben gezien. In de meetkunde is er echter een andere betekenis van de snijlijn:

Een lijn die een cirkel snijdt, is een lijn die een cirkel (of een curve) op twee verschillende punten snijdt.

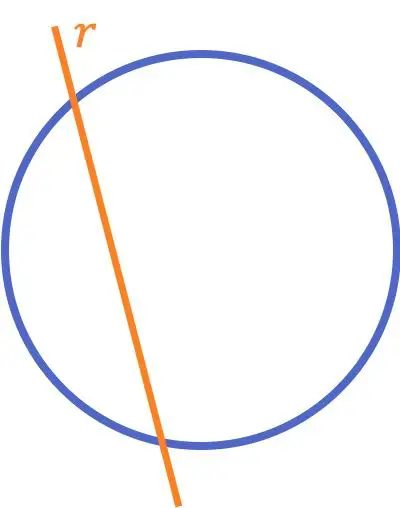
In tegenstelling tot het concept van twee elkaar kruisende lijnen dat gewoonlijk op de basisschool wordt onderwezen, wordt deze definitie van een lijn die een cirkel snijdt vaak bestudeerd in latere lessen, samen met alle relatieve posities van lijnen met cirkels.

Snijdende lijnen