Op deze pagina vind je de uitleg van de verschillende methoden die er bestaan om de relatieve positie van twee lijnen in het vlak (in R2) te bepalen. Daarnaast krijg je verschillende voorbeelden te zien en kun je oefenen met stap voor stap opgeloste oefeningen.
Wat is de relatieve positie van twee lijnen in het vlak?
Voordat je naar de relatieve posities tussen twee lijnen in het vlak kijkt, moet je uiteraard precies weten wat een lijn is. Je kunt dit vinden in de definitie van lijn .
Bij het werken in twee dimensies (in R2) zijn er dus 3 soorten mogelijke relatieve posities tussen twee lijnen:
snijdende lijnen

Twee snijdende lijnen hebben slechts één punt gemeen.
Parallelle lijnen

Twee lijnen zijn evenwijdig als ze geen gemeenschappelijk punt hebben. Tenminste, als ze elkaar nooit kruisen.
samenvallende lijnen

Twee lijnen zijn hetzelfde als al hun punten gemeenschappelijk zijn.
Aan de andere kant hangt de hoek tussen twee lijnen in het vlak ook af van hun relatieve positie:
- Snijdende lijnen snijden elkaar onder een hoek tussen 0º (niet inbegrepen) en 90º (inclusief). Als ze bovendien slechts een rechte hoek van 90 graden vormen, betekent dit dat de twee lijnen loodrecht staan.
- Evenwijdige lijnen vormen een hoek van 0º, omdat ze dezelfde richting hebben.
- En om dezelfde reden maken de samenvallende lijnen ook een hoek van 0° ertussen.
Als je wilt weten hoe de hoek tussen twee lijnen wordt berekend, kun je de formule voor de hoek tussen twee lijnen bekijken. Hier vindt u een gedetailleerde uitleg over hoe u de hoek tussen twee lijnen bepaalt, evenals verschillende voorbeelden en zelfs opgeloste oefeningen, zodat u het concept kunt oefenen en volledig kunt begrijpen.
Hoe de relatieve positie van twee lijnen in het vlak te vinden
Het kennen van de relatieve positie tussen twee lijnen in de tweedimensionale ruimte hangt af van hoe de lijnen worden uitgedrukt:
- Lijnrichtingsvectoren: als twee lijnen een verschillende richtingsvector hebben, moeten ze elkaar snijden. Aan de andere kant, als de coördinaten van hun richtingsvectoren gelijk of proportioneel zijn, kunnen ze parallel zijn of samenvallen (het is noodzakelijk om te controleren of ze een gemeenschappelijk punt hebben).
- Expliciete vergelijking: wanneer twee lijnen verschillende hellingen hebben
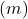
ze drogen. Integendeel, als de lijnen dezelfde helling hebben, maar een andere volgorde aan de oorsprong
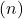
ze zijn parallel. Ten slotte raken twee lijnen verward als ze oorspronkelijk gelijke hellingen en ordinaten hebben.
- Algemene (of impliciete) vergelijking: twee lijnen met niet-proportionele coëfficiënten A en B zullen elkaar altijd snijden. Ze zullen echter parallel zijn als deze twee parameters evenredig zijn met elkaar, maar niet met de coëfficiënt C. En tenslotte, als de drie termen proportioneel zijn, impliceert dit dat de lijnen verward zijn.
Als je twijfels hebt over de vergelijkingen van de lijn hierboven, kun je de uitleg van de vergelijkingen van de lijn in het vlak raadplegen. Hier vind je de formule van alle lijnvergelijkingen, hoe ze worden berekend, voorbeelden en opgeloste oefeningen van lijnvergelijkingen.
In de volgende tabel vindt u een overzicht van de voorgaande eigenschappen:

Vervolgens zien we twee voorbeelden van hoe u de relatieve positie tussen twee lijnen kunt bepalen:
voorbeeld 1
- Zoek de relatieve positie tussen de volgende twee lijnen, gedefinieerd in de vorm van een expliciete vergelijking:
![]()
De twee lijnen hebben dezelfde helling:
![]()
Maar ze hebben aan de oorsprong verschillende computers:
![]()
Omdat ze dus dezelfde helling hebben maar verschillende snijpunten, zijn de lijnen evenwijdig .
Voorbeeld 2
- Bepaal de relatieve positie tussen de volgende twee lijnen, uitgedrukt met hun impliciete (of algemene) vergelijking:
![]()
Beide lijnen worden uitgedrukt als een expliciete vergelijking, daarom moeten we kijken of hun coëfficiënten proportioneel zijn:
![]()
De 3 termen van de lijnen zijn proportioneel, daarom vallen de lijnen samen .
Bepaal de relatieve positie van twee lijnen in het vlak met een stelsel vergelijkingen
Een andere manier om de relatieve positie tussen twee lijnen te kennen, is door het systeem van vergelijkingen te analyseren dat wordt gevormd door de vergelijkingen van de lijnen:
- Als het systeem een unieke oplossing heeft , kruisen de lijnen elkaar. Bovendien is het snijpunt van de twee lijnen de oplossing van het systeem.
- Als het een systeem zonder oplossing is, geeft dit aan dat de lijnen geen gemeenschappelijke punten hebben en daarom evenwijdige lijnen zijn.
- Als het systeem oneindig veel oplossingen heeft , betekent dit dat de lijnen alle punten gemeenschappelijk hebben en daarom snijdende lijnen zijn.
Voorbeeld 3
- Bereken de relatieve positie van de volgende twee lijnen met behulp van een stelsel vergelijkingen:
![]()
Om de relatieve positie van de twee lijnen te vinden, moeten we het volgende stelsel van lineaire vergelijkingen oplossen, gevormd door de twee lijnen:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-243b1e787e6532fbafbfca53d934f4ad_l3.png)
In dit geval zullen we het systeem oplossen met de substitutiemethode. We zullen daarom de variabele isoleren
![]()
uit de tweede vergelijking en vervang deze door de eerste vergelijking:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad3456c92c838f40d60afdb45e1eb2f3_l3.png)
![]()
![]()
![]()
![]()
![]()
En zodra we weten hoeveel het onbekende waard is
![]()
We vervangen de waarde ervan in de gevonden uitdrukking
![]()
![]()
![]()
We hebben daarom slechts één oplossing verkregen van het stelsel vergelijkingen dat uit de twee lijnen bestaat, dus de twee lijnen snijden elkaar . En het punt waar ze elkaar kruisen is de oplossing van het systeem, dat wil zeggen het punt
![]()
Problemen opgelost met de relatieve positie van twee lijnen in het vlak
Oefening 1
Bepaal of de volgende lijnen elkaar snijden, evenwijdig lopen of samenvallen:
![]()
Beide lijnen worden uitgedrukt als een impliciete (of algemene) vergelijking, daarom moeten we kijken of hun coëfficiënten proportioneel zijn:
![]()
Alleen de coëfficiënten A en B van de lijnen zijn evenredig met elkaar, en niet met de coëfficiënt C. Daarom zijn de twee lijnen evenwijdig .
Oefening 2
Zoek de relatieve positie tussen de volgende twee lijnen, uitgedrukt als parametervergelijkingen:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bafb951a2141722b0bbb7a1681f506ea_l3.png)
We zouden het stelsel van vergelijkingen gevormd door de twee lijnen kunnen oplossen om hun relatieve positie te vinden. Omdat ze echter de vorm hebben van parametrische vergelijkingen, kan men gemakkelijk hun richtingsvectoren vinden en als ze niet proportioneel zijn, betekent dit dat de lijnen elkaar snijden. En in dit geval zullen we niet zoveel tijd besteden aan het oplossen van een heel systeem van vergelijkingen.
Zodat de cartesische coördinaten van de richtingsvector van elke lijn de getallen vóór de parameter zijn
![]()
![]()
Zodra we de richtingsvectoren kennen, controleren we hun evenredigheid:
![]()
De richtingsvectoren zijn niet proportioneel, daarom kruisen de lijnen elkaar .
Oefening 3
Geef aan of de volgende lijnen elkaar snijden, evenwijdig of samenvallen en zoek ook een snijpunt ertussen (indien van toepassing).
![]()
De twee lijnen worden gedefinieerd door hun expliciete vergelijking en hebben verschillende hellingen:
![]()
Omdat ze verschillende hellingen hebben, kruisen de lijnen elkaar .
Omdat de lijnen elkaar snijden, zullen ze daarom één punt gemeen hebben en om dit te berekenen moeten we het stelsel vergelijkingen oplossen dat door de twee lijnen wordt gevormd:
![Rendered by QuickLaTeX.com \left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b3923ff74a214543ddd2cc44a42e3813_l3.png)
In dit geval zullen we het systeem oplossen met de egalisatiemethode omdat beide
![]()
zijn al verwijderd:
![]()
![]()
![]()
![]()
![]()
En zodra we het onbekende hebben
![]()
we vervangen de waarde ervan in elke uitdrukking van
![]()
om erachter te komen hoeveel het waard is:
![]()
![]()
Het snijpunt van de twee lijnen is dus het resultaat van het systeem:
![]()
Oefening 4
Bereken de waarde van de onbekenden
![]()
En
![]()
zodat de volgende twee lijnen evenwijdig zijn:
![]()
De lijnen worden beschreven in algemene (of impliciete) vergelijkingsvorm. Om de twee lijnen evenwijdig te laten zijn, moeten hun coëfficiënten A en B daarom proportioneel zijn, dat wil zeggen dat aan de volgende vergelijking moet worden voldaan:
![]()
We moeten daarom de vorige vergelijking oplossen om de waarde van het onbekende te verkrijgen
![]()
Om dit te doen, vermenigvuldigen we de breuken kruiselings:
![]()
![]()
![]()
Aan de andere kant, als de lijnen evenwijdig zijn, kunnen hun onafhankelijke termen niet evenredig zijn met de andere coëfficiënten:
![]()
Daarom lossen we, net als voorheen, de ongelijkheid op door de breuken kruiselings te vermenigvuldigen:
![]()
![]()
![]()
Kortom, zodat de twee lijnen evenwijdig zijn
![]()
moet 2 en zijn
![]()
kan elk reëel getal zijn, behalve 3.
Oefening 5
Zoek de expliciete vergelijking van de lijn evenwijdig aan de lijn
![]()
en wat er aan de overkant gebeurt
![]()
eerlijk zijn
![]()
![]()
Zodat de lijn evenwijdig is aan de lijn
![]()
beide moeten dezelfde helling hebben. en de helling van de lijn
![]()
is 2:
![]()
Daarom is de vergelijking van de lijn die we moeten vinden:
![]()
En zodra we de helling van de lijn kennen, kunnen we het y-snijpunt berekenen door het punt dat bij de lijn hoort in de vergelijking van de lijn te vervangen:
![]()
![]()
![]()
![]()
![]()
Dus de expliciete vergelijking van de lijn is:
![]()
Als je zo ver bent gekomen, betekent dit dat je de relatieve posities tussen twee lijnen in het plan al onder de knie hebt. Goed gedaan!
Maar één ding vragen velen zich af: wat is het nut van het kennen van de relatieve positie tussen twee lijnen?
Welnu, een van de toepassingen van de relatieve positie tussen lijnen is om de afstand tussen 2 lijnen te kunnen kennen, aangezien de berekening van de afstand tussen twee lijnen afhangt van hun relatieve positie:
- Als de lijnen elkaar snijden of samenvallen, is de afstand nul.
- Aan de andere kant, wanneer de lijnen evenwijdig zijn, moet een specifieke formule worden toegepast. Als je meer geïnteresseerd bent, kun je kijken hoe de afstand tussen twee parallelle lijnen wordt berekend.