Hoek tussen twee lijnen (formule)

Op deze pagina vindt u de uitleg over het berekenen van de hoek tussen twee lijnen (formule). Ook krijg je diverse voorbeelden te zien en daarnaast kun je oefenen met stap voor stap opgeloste oefeningen.

Wat is de hoek tussen twee lijnen?

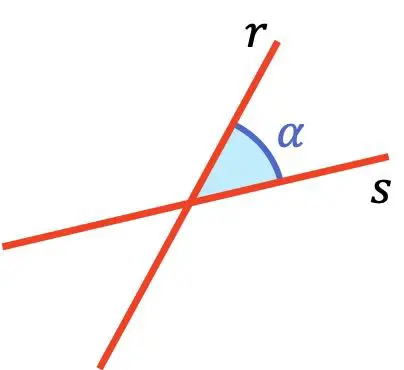
De hoek tussen twee lijnen is de kleinste hoek tussen deze twee lijnen.

In het plan zijn er vier soorten lijnen, afhankelijk van de hoek die ze ertussen vormen: snijdende lijnen (tussen 0º en 90º), loodrechte lijnen (90º), evenwijdige lijnen (0º) en samenvallende lijnen (0º).

snijdende lijnen

Snijlijnen snijden elkaar in een scherpe hoek tussen 0 en 90 graden.

Loodrechte rechte lijnen

Loodrechte lijnen snijden elkaar in een rechte hoek van 90 graden.

Parallelle lijnen

Parallelle lijnen raken elkaar nooit en maken er een hoek van 0° tussen.

samenvallende lijnen

Twee samenvallende lijnen hebben alle punten gemeen en daarom is er altijd een hoek van 0° tussen hen.

Concluderend is de berekening van de hoek tussen twee evenwijdige, samenvallende of loodrechte lijnen onmiddellijk: de evenwijdige lijnen en de samenvallende lijnen vormen een hoek van 0 graden omdat ze dezelfde richting hebben, en de loodrechte lijnen snijden elkaar met een hoek van 90 graden . Aan de andere kant, om de hoek tussen twee snijdende lijnen te vinden, moet je een formule toepassen (we zullen deze hieronder zien).

Hoe wordt de hoek tussen twee lijnen berekend?

Er zijn twee manieren om de hoek tussen twee lijnen te berekenen. De eerste methode gebruikt de richtingsvector van elke lijn en de tweede methode is gebaseerd op de helling van elke lijn.

Geen van beide procedures is beter dan de andere; beide zijn in feite vrij eenvoudig, maar afhankelijk van hoe de lijnen worden uitgedrukt, is de ene of de andere methode praktisch. Wij raden daarom aan dat u weet hoe u beide wiskundige methoden moet gebruiken.

Lijnvectororiëntatiemethode

De formule voor het berekenen van de hoek tussen twee lijnen met behulp van hun richtingsvectoren is:

Gegeven de richtingsvectoren van twee verschillende lijnen:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

De hoek tussen deze twee lijnen kan worden berekend met de volgende formule:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Goud

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

zijn de modules van de vectoren

$\vv{\text{u}}$

$\vv{\text{v}}$

respectievelijk.

Onthoud dat de formule voor de grootte van een vector is:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Laten we eens kijken hoe we de hoek tussen twee lijnen kunnen vinden met een voorbeeld:

Bereken de hoek tussen de volgende twee lijnen:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

Om de hoek tussen de twee lijnen te berekenen, moet je eerst de richtingsvector van elke lijn vinden.

het recht

$r$

wordt uitgedrukt in de vorm van een parametrische vergelijking , daarom zijn de componenten van de vector die de richting ervan markeert:

$\vv{r} = (-3,4)$

en de wet

$\displaystyle s$

wordt gedefinieerd in de vorm van een impliciete (of algemene) vergelijking, dus de coördinaten van zijn richtingsvector zijn:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Nu we de richtingsvector van elke lijn kennen, kunnen we de formule voor de hoek tussen twee lijnen gebruiken:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

We bepalen daarom de grootte van de twee vectoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

We voeren de vectorbewerkingen van de hoekformule uit:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

En ten slotte berekenen we de hoek gevormd door de twee lijnen met de inverse van de cosinus:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Onthoud dat u de inverse van de cosinus kunt berekenen met behulp van de rekenmachine met de sleutel

$\boxed{\cos ^{-1}}.$

helling methode

Om deze methode te begrijpen, moet je uiteraard de helling van de lijn kennen. U kunt dit concept in de link bekijken, waar u een gedetailleerde uitleg vindt van wat het betekent, hoe het wordt berekend, voorbeelden en opgeloste oefeningen van de helling van een lijn.

De formule voor het berekenen van de hoek tussen twee lijnen vanaf hun hellingen is:

Of twee verschillende lijnen:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

De hoek tussen deze twee lijnen kan worden bepaald met de volgende formule:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Goud

$m_1$

$m_2$

zijn de hellingen van de lijnen

$r_1$

$r_2$

respectievelijk.

Laten we eens kijken hoe we de hoek tussen twee lijnen kunnen berekenen met behulp van hun hellingen met een voorbeeld:

Zoek de hoek tussen de volgende twee lijnen:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

De helling van elke lijn is het getal vóór de variabele

$x:$

$m_r = 4$

$m_s = -3$

Daarom kan de hoek tussen de twee lijnen worden gevonden door de hellingsformule toe te passen:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

En tenslotte vinden we de hoek met het omgekeerde van de raaklijn:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Onthoud dat u de inverse van de tangens kunt berekenen met behulp van de rekenmachine met de sleutel

$\boxed{\tan ^{-1}}.$

We hebben zojuist een voorbeeld gezien met de hellingen van twee lijnen, uitgedrukt als een expliciete vergelijking, maar als ze de vorm hadden van een punthellingsvergelijking, zou dezelfde procedure moeten worden gebruikt.

Hoekproblemen tussen twee lijnen oplossen

Oefening 1

Bepaal de hoek gevormd door de volgende twee lijnen:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

zie oplossing

In dit geval zullen we de richtingsvectormethode gebruiken. Daarom moeten we eerst de richtingsvector van elke lijn vinden. Beide lijnen worden uitgedrukt als parametervergelijkingen, dus de componenten van hun richtingsvectoren zijn de termen vóór de parameter

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Nu we de richtingsvector van elke lijn kennen, kunnen we de formule voor de hoek tussen twee lijnen gebruiken:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

We bepalen daarom de grootte van de twee vectoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

We lossen het scalaire product op tussen de twee vectoren van de teller en de vermenigvuldiging van de modules van de noemer:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

En ten slotte vinden we de hoek gevormd door de twee lijnen door de inverse van de cosinus te doen:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Oefening 2

Zoek de hoek tussen de volgende twee lijnen:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

zie oplossing

We zullen dit probleem oplossen met behulp van de richtingsvectormethode, dus eerst moeten we de richtingsvector van elke lijn vinden. het recht

$r$

wordt uitgedrukt in de vorm van een algemene (of impliciete) vergelijking, zodat de componenten van de vector die de richting ervan markeren zijn:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

en de wet

$\displaystyle s$

wordt gedefinieerd in de vorm van een continue vergelijking, dus de cartesische coördinaten van zijn richtingsvector zijn de getallen van de noemers:

$\vv{s} = (6,3)$

Zodra we de richtingsvector van elke lijn kennen, kunnen we de formule voor de hoek tussen twee lijnen gebruiken:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

We bepalen daarom de modules van de twee vectoren:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

We voeren de bewerkingen uit tussen vectoren van de hoekformule:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

En ten slotte berekenen we de hoek gevormd door de twee lijnen met de inverse van de cosinus:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Oefening 3

Wat is de hoek tussen de volgende twee lijnen?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

zie oplossing

In dit geval zullen we de methode van de hellingen van de lijnen gebruiken om de hoek te achterhalen die ze maken, aangezien de lijnen de vorm hebben van een expliciete vergelijking.

De helling van elke lijn is het getal dat bij de onafhankelijke variabele hoort

$x:$

$m_r = -2$

$m_s = 5$

Daarom kan de hoek tussen de twee lijnen worden bepaald door de hellingsformule toe te passen:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

En tenslotte vinden we de hoek tussen de twee lijnen door de raaklijn om te keren:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Oefening 4

Zoek de vergelijking van de lijn die door het punt gaat

$P(5,-1)$

en maakt een hoek van 45° met de lijn

$r.$

Wees gezegd:

$\displaystyle r: \ y=2x+4$

zie oplossing

Om het probleem op te lossen, bellen wij

$s$

aan de rechterkant die we gaan berekenen. Bovendien zullen we de hellingsmethode gebruiken omdat we de helling van de lijn kennen

$r:$

$m_r=2$

Uit de formule voor de hoek tussen twee lijnen (hellingmethode) kunnen we de waarde van de helling van de lijn verkrijgen

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

We vervangen de bekende waarden in de formule:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

En we proberen de resulterende vergelijking op te lossen:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

De absolute waarde van de vergelijking maakt het enigszins moeilijk op te lossen, omdat je zowel de positieve als de negatieve opties moet analyseren:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

We hebben daarom twee mogelijke oplossingen: een lijn met helling -3 en een andere lijn met helling een derde.

De formule voor de punt-hellingvergelijking van een lijn is:

$y-y_0=m(x-x_0)$

Daarom kunnen we, zodra we de helling van de twee mogelijke lijnen kennen, de punt-hellingsvergelijking van elke lijn schrijven met het punt waar ze doorheen moeten gaan volgens de verklaring:

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

Wat is de hoek tussen twee lijnen?

Hoe wordt de hoek tussen twee lijnen berekend?

Lijnvectororiëntatiemethode

helling methode

Hoekproblemen tussen twee lijnen oplossen

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren