Vergelijkingspunt – helling van de lijn

Op deze pagina vindt u de formule voor de punt-hellingsvergelijking van de lijn en ook de verschillende manieren om deze te berekenen. Daarnaast kun je verschillende voorbeelden zien en oefenen met oefeningen die stap voor stap worden opgelost.

Formule voor de punt-hellingvergelijking van de lijn

De punt-hellingvergelijking van een lijn is een manier om een lijn wiskundig uit te drukken. In het bijzonder hebt u alleen de helling en de coördinaten van een punt op de lijn nodig om de punt-hellingsvergelijking van een lijn te vinden.

De formule voor de punt-hellingvergelijking van de lijn is als volgt:

$y-y_0=m(x-x_0)$

Goud

$m$

is de helling van de lijn en

$x_0, y_0$

zijn de coördinaten van een punt op de lijn

$P(x_0,y_0).$

Laten we eens kijken hoe de punt-hellingsvergelijking van de lijn wordt berekend aan de hand van een voorbeeld:

Schrijf de punt-hellingvergelijking van de lijn die door het punt gaat
$P(2,-1)$

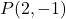
en helling m=3.

De formule voor de punt-hellingvergelijking van de lijn is als volgt:

$y-y_0=m(x-x_0)$

In dit geval vertelt de verklaring ons dat de helling van de lijn m=3 is, dus de vergelijking van de lijn zal als volgt zijn:

$y-y_0=3(x-x_0)$

Verder weten we ook dat de lijn door het punt gaat

$P(2,-1)$

, moeten we daarom de coördinaten van dit punt in de vergelijking vervangen:

$P(2,-1)$

$y-y_0=3(x-x_0) \ \xrightarrow{x_0=2 \ ; \ y_0=-1} \ y-(-1)=3(x-2)$

De punt-hellingsvergelijking van de lijn is daarom:

$\bm{y+1=3(x-2)}$

Houd er rekening mee dat er naast de punt-hellingsvergelijking ook andere manieren zijn om een lijn analytisch uit te drukken: de vectorvergelijking, parametervergelijkingen, de continue vergelijking, de impliciete vergelijking (of algemeen) en de expliciete vergelijking van een lijn. Als u meer geïnteresseerd bent, kunt u op onze website bekijken wat elk van hen is.

Wat betekent de helling van een lijn?

Zoals we zagen bij de definitie van de punt-hellingvergelijking van een lijn, de parameter

$m$

is de helling van de lijn. Maar echt… wat betekent de helling van een lijn? Laten we dit eens bekijken aan de hand van de grafische weergave van een lijn:

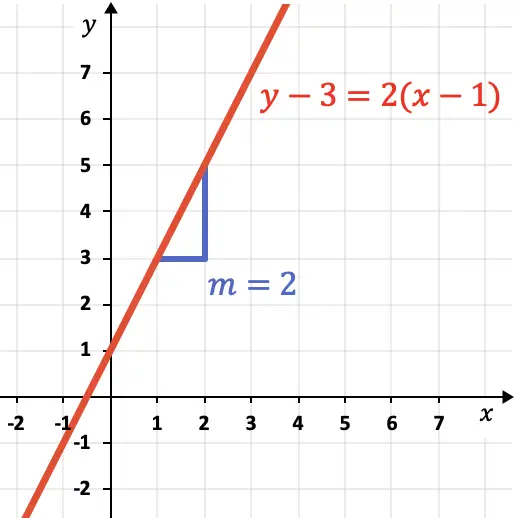
Wat is de punt-hellingvergelijking van een lijn?

De helling van de lijn geeft de steilheid aan. Zoals u kunt zien aan de grafieklijn,

$m$

is gelijk aan 2 omdat de lijn 2 verticale eenheden stijgt voor 1 horizontale eenheid.

Het is duidelijk dat als de helling positief is, de functie toeneemt (omhoog), maar als de helling negatief is, neemt de functie af (omlaag).

Hoe de helling van een lijn te berekenen

Verder zijn er 3 verschillende manieren om de helling van een lijn numeriek te bepalen:

Gegeven twee verschillende punten op de lijn
$P_1(x_1,y_1)$

En

$P_2(x_2,y_2),$

De helling van de lijn is gelijk aan:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Ja
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

is de richtingsvector van de lijn, de helling is:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Ja
$\alpha$

is de hoek gevormd door de lijn met de abscis-as (X-as), de helling van de lijn is gelijk aan de raaklijn van genoemde hoek:

$m = \text{tg}(\alpha )$

formule voor de expliciete vergelijking van de lijn

Relatieve positie van lijnen

Ten slotte wordt de helling van een lijn ook gebruikt om de relatie tussen verschillende lijnen te kennen. Omdat twee parallelle lijnen dezelfde helling hebben en, aan de andere kant, als de helling van één lijn het negatieve omgekeerde is van de helling van een andere lijn, betekent dit dat deze twee lijnen loodrecht staan.

Bereken de punt-hellingvergelijking van de lijn die door twee punten gaat

Een veel voorkomend probleem is het bepalen van de punt-hellingvergelijking vanuit twee punten die tot de lijn behoren. Laten we eens kijken hoe het wordt opgelost aan de hand van een voorbeeld:

Zoek de punt-hellingsvergelijking van de lijn die door de volgende twee punten gaat:

$P_1(5,2) \qquad P_2(3,6)$

Om de punt-hellingsvergelijking van de lijn te vinden, moeten we bepalen wat de helling van de lijn is. We berekenen dus de helling van de lijn met behulp van de dubbele puntformule:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{6-2}{3-5} = \cfrac{4}{-2}= -2$

De punt-hellingvergelijking van de lijn zal dus als volgt zijn:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Daarom hoeven we alleen de cartesiaanse coördinaten van een punt op de lijn in de vergelijking in te vullen:

$P_1(5,2)$

$y-y_0=-2(x-x_0) \ \xrightarrow{x_0=5 \ ; \ y_0=2} \ y-2=-2(x-5)$

$\bm{y-2=-2(x-5)}$

Het is ook goed als we het andere punt van de uitspraak in de vergelijking van de lijn plaatsen:

$P_1(3,6)$

$y-6=-2(x-3)$

Zoek de punt-hellingvergelijking van een lijn uit de grafiek

Zoals we in de bovenstaande paragrafen hebben gezien, zijn er verschillende manieren om de punt-hellingsvergelijking van een lijn numeriek te vinden. Het is echter ook grafisch te vinden. Laten we eens kijken hoe dit wordt gedaan aan de hand van een voorbeeld:

Bepaal de punt-hellingvergelijking van de lijn in de volgende grafiek:

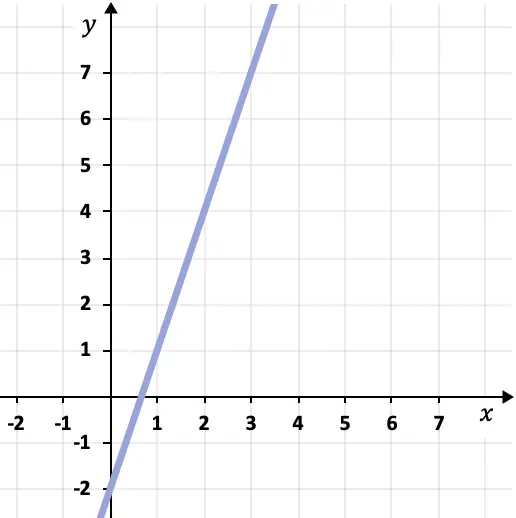
Om de punt-hellingvergelijking voor de getekende lijn te bepalen, moeten we de helling ervan en een punt op de lijn vinden.

In dit geval is de helling van de lijn gelijk aan 3, omdat de lijn voor elke horizontale eenheid 3 verticale eenheden stijgt.

$m = 3$

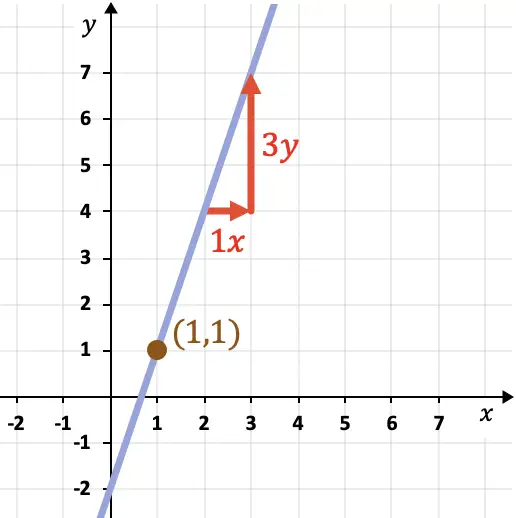
Vervolgens hebben we een punt op de lijn nodig. Om dit te doen, kunnen we elk punt op de grafiek kiezen waar de lijn doorheen gaat, bijvoorbeeld het punt (1,1).

$P(1,1)$

Daarom kunnen we nu de punt-hellingsvergelijking van de lijn vinden door de formule toe te passen:

$y-y_0=m(x-x_0)$

$y-1=3(x-1)$

grafisch de helling van het vergelijkingspunt van een lijn bepalen

Problemen met punt-hellingvergelijkingen opgelost

Oefening 1

Schrijf de punt-hellingvergelijking van de lijn die door het punt gaat

$P(1,4)$

en de helling ervan is

$m=-2.$

zie oplossing

De formule voor de punt-hellingsvergelijking van de lijn is:

$y-y_0=m(x-x_0)$

In dit geval vertelt de verklaring ons dat de helling van de lijn m=-2 is, dus de vergelijking van de lijn zal als volgt zijn:

$y-y_0=-2(x-x_0)$

Verder weten we uit de stelling ook dat de lijn door het punt gaat

$P(1,4)$

, is het daarom voldoende om de coördinaten van het punt in de vergelijking van de lijn te vervangen:

$P(1,4)$

$\bm{y-4=-2(x-1)}$

Oefening 2

Wat is de punt-hellingsvergelijking van de lijn die door de volgende twee punten gaat?

$P_1(1,6) \qquad P_2(4,0)$

zie oplossing

Om de punt-hellingsvergelijking van de lijn te vinden, moeten we bepalen wat de helling van de lijn is. We berekenen daarom de helling van de lijn met de formule:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{0-6}{4-1} = \cfrac{-6}{3}= -2$

De punt-hellingvergelijking van de lijn zal dus als volgt zijn:

$y-y_0=m(x-x_0)$

$y-y_0=-2(x-x_0)$

Daarom hoeven we alleen de coördinaten van een punt op de lijn in de vergelijking in te vullen:

$P_1(1,6)$

$\bm{y-6=-2(x-1)}$

Het zou ook correct zijn geweest om het andere punt van de verklaring in de vergelijking te verwerken:

$y=-2(x-4)$

Oefening 3

Zoek de punt-hellingsvergelijking van de lijn die door de volgende twee punten gaat:

$P_1(1,-2) \qquad P_2(2,3)$

zie oplossing

Om de punt-hellingsvergelijking van de lijn te vinden, moet u eerst de helling ervan berekenen:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{3-(-2)}{2-1} = \cfrac{3+2}{1}=\cfrac{5}{1}= 5$

De punt-hellingvergelijking van de lijn zal dus als volgt zijn:

$y-y_0=m(x-x_0)$

$y-y_0=5(x-x_0)$

Daarom hoeven we alleen de coördinaten van een punt op de lijn in de vergelijking in te vullen:

$P_1(1,-2)$

$y-(-2)=5(x-1)$

$\bm{y+2=5(x-1)}$

Het is ook correct om het andere punt in de bewering in de vergelijking van de lijn te plaatsen:

$y-3=5(x-2)$

Oefening 4

Bereken de punt-hellingvergelijking voor de lijn die een hoek van 45° vormt met de X-as en door de coördinaatoorsprong gaat.

zie oplossing

Als de lijn een hoek van 45 graden maakt met de OX-as, is de helling:

$m = \text{tg}(45º) = 1$

$y-y_0=1(x-x_0)$

$y-y_0=x-x_0$

En zodra we de helling van de lijn kennen, kunnen we de punt-hellingvergelijking vinden door een punt op de lijn in de vergelijking te vervangen. Bovendien vertelt de verklaring ons dat de lijn door de coördinaatoorsprong gaat, wat betekent dat deze door het punt (0,0) gaat. Nog:

$P(0,0)$