Op deze pagina vindt u de uitleg van de regel (of wet) van het parallellogram. Daarnaast ziet u verschillende voorbeelden van het optellen en aftrekken van vectoren met behulp van de parallellogramregel, evenals toepassingen in de echte wereld.
Wat is de parallellogramregel?
Zoals je al weet, kunnen vectorgrootheden niet op dezelfde manier worden opgeteld of afgetrokken als reële getallen, omdat ze twee componenten (in R2) of drie componenten (in R3) hebben en omdat vectoren verschillende richtingen kunnen hebben. Daarom zijn er andere methoden nodig om vectorbewerkingen uit te voeren, zoals de parallellogramregel, die uit het volgende bestaat:
In de wiskunde is de parallellogramregel een procedure voor het optellen of aftrekken van twee vectoren van hun grafische weergave.
De parallellogrammethode wordt ongetwijfeld het meest gebruikt bij het optellen en aftrekken van vectoren (grafisch), omdat het een zeer gemakkelijke techniek is om te gebruiken. In de natuurkunde wordt het bijvoorbeeld gebruikt om krachten op te tellen en af te trekken.
Aan de andere kant varieert de regel enigszins, afhankelijk van of we vectoren willen optellen of aftrekken, dus hieronder zullen we beide versies afzonderlijk uitleggen.
Parallellogramregel voor het optellen van twee vectoren
Als we twee vectoren grafisch willen optellen, zijn de stappen om de parallellogramregel of -wet toe te passen:
- Eerst tekenen we de vectoren en plaatsen ze op hetzelfde toepassingspunt, dat wil zeggen dat we de oorsprong van beide vectoren op hetzelfde punt plaatsen.
- Vervolgens tekenen we aan het einde van de ene vector een lijn evenwijdig aan de andere vector. En we herhalen de stap met de andere vector. We krijgen daarom de tekening van een parallellogram (vandaar de naam van de regel).
- Ten slotte zal de uit de som resulterende vector de diagonaal zijn van het parallellogram, die loopt van de gemeenschappelijke oorsprong van de vectoren naar het snijpunt van de twee parallelle lijnen.
In het volgende algemene voorbeeld kunt u zien hoe de parallellogramregel wordt gebruikt:

Als je wilt oefenen met de parallellogramregel, kun je in de volgende link meer voorbeelden en verschillende opgeloste vectoroptellingoefeningen raadplegen. Op deze pagina vindt u ook andere methoden om vectoren grafisch toe te voegen en zelfs hoe u ze numeriek kunt toevoegen.
Parallellogramregel voor het aftrekken van twee vectoren
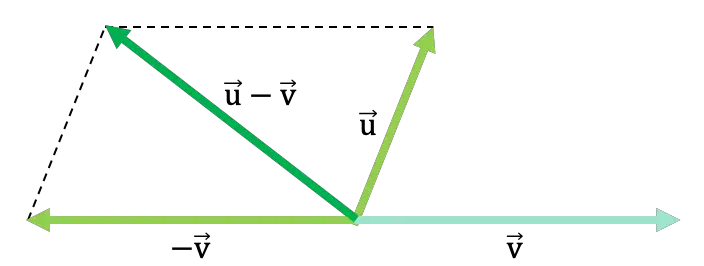
De parallellogramregel of -methode wordt ook gebruikt om twee vectoren van een grafiek af te trekken. De stappen voor het vectoraftrekken zijn dus:
- Eerst vertegenwoordigen we de twee vectoren in de grafiek en plaatsen ze op hetzelfde toepassingspunt, dat wil zeggen dat we de oorsprong van beide vectoren op hetzelfde punt plaatsen.
- Ten tweede tekenen we de tegenovergestelde vector van de vector die wordt afgetrokken in de bewerking, of met andere woorden: we keren de vector om die wordt afgetrokken.
- Vervolgens tekenen we een lijn evenwijdig aan de tekenveranderingsvector aan het einde van de vector, wat neerkomt op . En we herhalen het proces met de andere vector. Zodat we de tekening van een parallellogram krijgen (vandaar de naam van de regel).
- Ten slotte zal het resultaat van de aftrekking de vector zijn die loopt van de gemeenschappelijke oorsprong van de twee vectoren naar het punt waar de twee parallelle lijnen elkaar kruisen.
Kijk naar het volgende algemene voorbeeld waarin twee vectoren worden afgetrokken door de parallellogramwet:
In de volgende link kun je meer voorbeelden zien van vectoraftrekken met de parallellogramregel, je kunt ook oefenen met opgeloste vectoraftrekkingsoefeningen . Daarnaast zul je andere technieken vinden om vectoren van hun grafiek af te trekken en, ten slotte, hoe ze numeriek worden afgetrokken.
Ten slotte, als de uitleg van deze techniek nuttig voor u was, zult u zeker ook geïnteresseerd zijn om te weten wat de rechterhandregel is. Op de linkpagina kunt u zien wat het is, voor welke vectorbewerking het wordt gebruikt en welke verschillende varianten van deze regel bestaan.