Hoe de modulus van een vector te berekenen

Op deze pagina ziet u de uitleg van de grootte van een vector en hoe u deze kunt berekenen met de formule. U kunt ook zien hoe u de module kunt vinden vanuit twee punten: de oorsprong en het einde. Daarnaast ontdek je hoe je de componenten van een vector kunt bepalen op basis van zijn modulus en de eigenschappen van de modulus van een vector. Je kunt zelfs oefenen met voorbeelden, oefeningen en stap-voor-stap problemen.

Wat is de modulus van een vector?

De grootte van een vector vertegenwoordigt de afstand tussen zijn oorsprong en zijn einde. Daarom is de grootte van een vector gelijk aan de lengte van de vector.

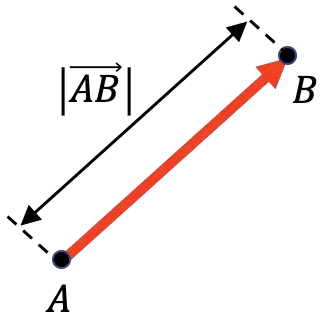
Zoals je kunt zien in de grafische weergave hierboven, wordt de grootte van een vector gesymboliseerd door een verticale balk aan elke kant van de vector:

$\lvert \vv{AB}\rvert$

Aan de andere kant is de modulus van een vector hetzelfde als de norm van een vector , dus je kunt het ook zo geschreven zien. Dit is de reden waarom er wiskundigen zijn die ook de module van een vector weergeven met twee verticale balken aan elke kant:

$\lvert \lvert \vv{AB}\rvert\rvert$

Formule voor de modulus van een vector

Om de grootte van een vector in het vlak te vinden, moeten we de volgende formule toepassen:

Om de grootte van een vector te bepalen, moeten we de (positieve) vierkantswortel berekenen van de som van de kwadraten van zijn componenten. Met andere woorden, als we de volgende vector hebben:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

De module is:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

We berekenen bijvoorbeeld de grootte van de volgende vector met behulp van de formule:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Bereken de grootte van een vector met de coördinaten van zijn oorsprong en einde

We hebben zojuist gezien hoe de grootte van een vector wordt bepaald als we de componenten ervan kennen, maar wat zou er gebeuren als we alleen de punten zouden kennen waar hij begint en waar hij eindigt?

Om dus de grootte van een vector te berekenen op basis van de coördinaten van zijn oorsprong en zijn einde, moet u deze twee stappen volgen:

Eerst vinden we de componenten van de vector. Om dit te doen, moeten we het extremum minus de oorsprong aftrekken.
En dan berekenen we de module van de vector die we hebben verkregen met de formule die we in de vorige sectie hebben gezien.

Laten we eens kijken hoe dit wordt gedaan aan de hand van een voorbeeld:

Bereken de grootte van de vector waarvan de oorsprong het punt is
$A(2,1)$

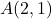
en als laatste punt

$B(-1,4).$

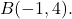
We moeten eerst de componenten van de vector vinden, dus trekken we het eindpunt minus de oorsprong af:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Zodra we de vector kennen, berekenen we de grootte ervan met behulp van de vectorgrootteformule:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

En we laten het resultaat als een vierkantswortel staan, omdat het niet exact is.

Hoe de componenten van een vector te berekenen op basis van zijn modulus

We hebben gezien hoe we de grootte van een vector uit zijn componenten kunnen halen, maar het proces kan ook worden omgekeerd. Met andere woorden, we kunnen de componenten van een vector berekenen via zijn modulus.

Het proces van het vinden van de componenten van een vector op basis van zijn grootte wordt vectorontbinding genoemd. Om een vector te ontbinden hebben we uiteraard de grootte ervan nodig, en de hoek die deze vormt met de abscis-as (X-as).

Zodat de X- en Y-componenten van de vector kunnen worden berekend met de trigonometrische verhoudingen:

Zoals je in de afbeelding kunt zien, vormt de grootte van een vector een rechthoekige driehoek met zijn componenten, zodat de elementaire formules van de trigonometrie kunnen worden toegepast.

Er moet rekening mee worden gehouden dat, in tegenstelling tot de modulus van een vector, de componenten ervan negatief kunnen zijn omdat de sinus en cosinus negatieve waarden kunnen aannemen.

Als voorbeeld zullen we de vectorontleding oplossen van de vector waarvan de grootte en hoek met de OX-as zijn:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

De horizontale component van de vector is gelijk aan de module vermenigvuldigd met de cosinus van de hoek:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

En de verticale component van de vector is gelijk aan het vermenigvuldigen van de module met de sinus van de hoek:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

De vector is dus de volgende:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Moduluseigenschappen van een vector

Modulus is een type vectorbewerking met de volgende kenmerken:

De grootte van een vector kan nooit negatief zijn , hij zal altijd gelijk zijn aan of groter zijn dan 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

In feite is de enige vector die bestaat met een magnitude nul, de nulvector, dat wil zeggen de vector

$\vv{\text{u}}= (0,0) .$

De grootte van het product van een vector met een reëel getal (of een scalair) is gelijk aan het vermenigvuldigen van de absolute waarde van de scalair met de grootte van de vector. Daarom geldt de volgende gelijkheid:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

De driehoeksongelijkheid wordt geverifieerd: de modulus van de som van twee vectoren is kleiner dan of gelijk aan de som van hun modules afzonderlijk.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Bovendien is de grootte van de som van twee vectoren gerelateerd aan het puntproduct door de volgende vergelijking:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

eenheid Vector

In de wiskunde is een eenheidsvector een vector waarvan de modulus gelijk is aan één.

$\lvert \vv{\text{u}} \rvert=1$

Daarom is de lengte van een eenheidsvector één eenheid.

Het lijkt misschien erg moeilijk voor een vector om een modulus van precies 1 te hebben, maar het is eigenlijk eenvoudig om dit type vector te vinden:

Om de eenheidsvector van een vector te vinden, deelt u deze eenvoudigweg door zijn modulus:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Goud

$\vv{\text{v}}_u$

is de eenheidsvector van

$\vv{\text{v}},$

$\lvert \vv{\text{v}} \rvert$

uw module.

De eenheidsvector wordt ook versor of genormaliseerde vector genoemd.

Bovendien heeft de eenheidsvector dezelfde richting en richting als de originele vector.

We berekenen bijvoorbeeld de eenheidsvector van de volgende vector:

$\vv{\text{v}}=(1,-1)$

Om de vector te normaliseren, moeten we eerst de grootte ervan berekenen:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

En ten slotte berekenen we de eenheidsvector door de oorspronkelijke vector te delen door zijn modulus:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Opgeloste vectormodule-oefeningen

Oefening 1

Bereken de grootte van de volgende vector:

$\vv{a}=(6,8)$

zie oplossing

Om de module van de vector te berekenen, moeten we de formule ervan toepassen:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Oefening 2

Rangschik de volgende vectoren van kort naar langst.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

zie oplossing

De lengte van een vector is gelijk aan zijn grootte. Daarom moeten we de moduli van alle vectoren berekenen:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

De vectoren gerangschikt van de kleinste naar de grootste lengte (of module) zijn dus:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Oefening 3

Bepaal de grootte van de vector waarvan de oorsprong het punt is

$A(-3,2)$

en als laatste punt

$B(7,-4).$

zie oplossing

Om de module ervan te berekenen, moet je eerst de vector vinden. Om dit te doen, trekken we het extremum minus de oorsprong af:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Zodra we de vector kennen, wordt de modulus berekend met behulp van de modulusformule:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Oefening 4

Ontleed de volgende vector en vind de componenten ervan:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

zie oplossing

De horizontale component van de vector is gelijk aan de module vermenigvuldigd met de cosinus van de hoek:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

En de verticale component van de vector is gelijk aan het vermenigvuldigen van de module met de sinus van de hoek:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

De vector is dus de volgende:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

In dit geval zijn de twee componenten identiek, dat wil zeggen dat de hellingshoek van de vector 45 graden is.

Oefening 5

Bereken de vector met dezelfde richting en richting als de volgende vector maar met module 1.

$\vv{a} = (-4,3)$

zie oplossing

De vector met dezelfde richting en dezelfde richting maar met module 1 is de eenheidsvector. Om het te berekenen, vinden we eerst de module van de vector:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$