Het getal van Euler (ook bekend als de constante van Euler) is een belangrijk en essentieel wiskundig getal op verschillende gebieden van de wiskunde, waaronder getaltheorie, topologie, groepentheorie en functietheorie. Het wordt weergegeven door de Griekse letter “e” en de geschatte waarde is 2,71828.
Het getal e volgt uit de formule voor de exponentiële functie en is een fundamenteel getal in de complexe getaltheorie.
Het is ook een natuurlijk getal dat voorkomt bij het oplossen van veel wiskundige problemen, waaronder het berekenen van waarschijnlijkheid en het modelleren van groei- en vervalprocessen.
Wat is de oorsprong van het getal van Euler?
Het Eulergetal is vernoemd naar de Zwitserse wiskundige Leonhard Euler (1707-1783), die een van de grootste wiskundigen aller tijden was en wordt beschouwd als de vader van de moderne wiskunde.
Euler heeft waardevolle bijdragen geleverd aan veel gebieden van de wiskunde, waaronder getaltheorie, meetkunde, calculus, natuurkunde en astronomie.
Hij was het die het getal e (het getal van Euler genoemd) voor het eerst definieerde en gebruikte in zijn werk over de berekening en theorie van logaritmen. Eulers formule voor complexe getallen is ook een van zijn meest opmerkelijke bijdragen aan de wiskunde.
Hoe wordt deze waarde verkregen?
In feite zijn er verschillende methoden om het Euler-getal te berekenen. Het is echter de moeite waard te vermelden dat geen van beide methoden een exact resultaat oplevert. Daarom is de nummering continu en oneindig, maar wordt deze niet herhaald.
In feite zijn er momenteel meer dan 1 biljoen getallen bekend die het getal e vormen. De oneindige reeks die het Eulergetal definieert is:

Goud “!” is faculteit, die wordt gedefinieerd als het product van alle natuurlijke getallen tot dat getal. Bijvoorbeeld:
5! = 5 4 3 2 1 = 120
We kunnen deze reeks grafisch zien als de som van een reeks rechthoeken met een hoogte van 1 en een afnemende breedte, waarbij de breedte van elke rechthoek 1/n! is, waarbij n het aantal faculteiten is.
Als we het aantal rechthoeken in de som vergroten, komt de benadering van het gebied onder de curve van de exponentiële functie steeds dichter bij het getal van Euler.
Samenvattend is het getal van Euler een getal dat voortkomt uit de som van een oneindige reeks en dat van fundamenteel belang is voor veel gebieden van de wiskunde. Hoewel het een irrationeel getal is, is de geschatte waarde 2,71828.
Het is belangrijk om in gedachten te houden dat Euler deze methode zelf heeft geïmplementeerd om e tot 18 decimalen te berekenen.
Een andere manier om het te berekenen:
We kunnen de geschatte waarde van het Eulergetal op een lijn berekenen met behulp van een reeks eindige termen . Als we bijvoorbeeld de eerste oneindige reeks nemen die hierboven is gedefinieerd:

We kunnen de geschatte waarde berekenen door de eerste termen van de reeks toe te voegen. Als we bijvoorbeeld de eerste zes termen toevoegen:
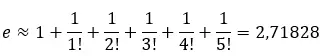
We kunnen deze reeks op een lijn uitzetten om te zien hoe deze de geschatte waarde van 2,71828 benadert.
Grafisch kan de lijn die het Eulergetal vertegenwoordigt, worden getekend als een reeks rechthoeken met een hoogte van 1 en afnemende breedte, waarbij de breedte van elke rechthoek 1/n! is, waarbij n het aantal faculteiten is.
Als we het aantal rechthoeken in de som vergroten, komt de benadering van het gebied onder de curve van de exponentiële functie steeds dichter bij het getal van Euler.
Exponentiële vergelijkingen met het getal van Euler
Exponentiële vergelijkingen met het Eulergetal kunnen worden gebruikt om een grote verscheidenheid aan verschijnselen in wetenschappen zoals natuurkunde, biologie en economie te modelleren. Hier zijn enkele voorbeelden:
Exponentiële groei en verval
Dit model beschrijft de snelheid waarmee een bevolking groeit of afneemt , of de snelheid waarmee een giftige stof afbreekt.
Als een bevolking bijvoorbeeld met 5% per jaar groeit, kan de omvang ervan worden beschreven met de formule:
P(t) = P0 · e 0,05t , waarbij P0 de initiële populatiegrootte is.
Radioactief vervalmodellen
Dit model beschrijft de snelheid waarmee radioactieve atomen in de loop van de tijd vervallen.
De formule is als volgt:
N(t) = N0 e -λt
waarbij N0 het initiële aantal atomen is, is λ een constante die afhangt van het radioactieve materiaal en t de tijd.
Dit zijn slechts enkele voorbeelden van hoe exponentiële vergelijkingen met het getal van Euler in de praktijk kunnen worden gebruikt. Er zijn veel andere gebieden waarop exponentiële vergelijkingen nuttig en relevant zijn.
Wat zijn de toepassingen van het getal van Euler?
Het Eulergetal heeft een breed scala aan toepassingen op verschillende gebieden van wiskunde en wetenschappen. Enkele velden waarin het getal e wordt gebruikt zijn:
- Berekening en wiskundige analyse : het wordt gebruikt bij de studie van exponentiële en logaritmische functies en bij de resolutie van differentiaalvergelijkingen.
- Getaltheorie – gebruikt bij de studie van de verdeling van priemgetallen en bij het oplossen van problemen die verband houden met de getaltheorie.
- Waarschijnlijkheid en statistiek : het wordt gebruikt bij het oplossen van problemen met betrekking tot de kansverdeling en het schatten van verwachte waarden.
- Cryptografie – Gebruikt bij de studie van coderings- en decoderingsalgoritmen.
- Natuurkunde – gebruikt om problemen op te lossen die verband houden met de thermodynamica, kwantummechanica en statistische natuurkunde.
- Chemie : het wordt gebruikt bij het oplossen van problemen die verband houden met chemische thermodynamica en chemische kinetiek.
Euler’s formule voor complexe getallen
De formule van Euler voor complexe getallen legt een verband tussen trigonometrische en exponentiële functies. De formule is geschreven:

Waar “e” de basis is van natuurlijke logaritmen, “i” de denkbeeldige eenheid is, “x” een reëel getal is, en “cos” en “sin” respectievelijk de goniometrische functies cosinus en sinus zijn.
Deze formule is zeer nuttig op veel gebieden van de wiskunde, waaronder de getaltheorie, de functietheorie en de complexiteitstheorie, en heeft een grote verscheidenheid aan toepassingen in de techniek, natuurkunde en economie.
Een praktisch voorbeeld van het gebruik ervan is de weergave van signalen en systemen in Fourier-analyse, waarbij periodieke signalen worden weergegeven als een som van complexe sinusoïdale signalen.
De formule van Euler wordt gebruikt om te beschrijven hoe deze complexe signalen zich verhouden tot de feitelijke trigonometrische functies die de individuele sinusoïdale signalen beschrijven.
Het getal van Euler en de samengestelde rente
Samengestelde rente is een financieel concept dat het proces beschrijft waarbij een som geld, de zogenaamde hoofdsom, rente verdient op rente die in de loop van de tijd toeneemt.
Met andere woorden: de rente die wordt verdiend met een belegging komt niet alleen voort uit het startkapitaal, maar ook uit de rente die in voorgaande perioden is verdiend.
Het Euler-getal en de samengestelde rente zijn gerelateerd omdat de formule voor het berekenen van de samengestelde rente het Euler-getal gebruikt. De formule voor samengestelde rente is:
A = P e rt
Waar A het eindbedrag is, is P de hoofdsom, r de rentevoet, t de tijd en e het Eulergetal. Op deze manier is het Eulergetal een belangrijke factor in de wiskundige formulering voor het berekenen van samengestelde rente.
Een voorbeeld van het berekenen van samengestelde rente met concrete cijfers zou zijn:
Stel dat we een investering hebben van € 1.000,- tegen een rente van 5% per jaar gedurende 2 jaar. De formule om samengestelde rente te berekenen zou zijn:
A = P e rt = 1000 e 0,05 2 = 1000 1,1025 = €1102,5.
Dit betekent dat na 2 jaar ons startkapitaal van € 1.000,- dankzij de gegenereerde samengestelde rente zal zijn gestegen naar € 1.102,50.
Voorbeelden van wiskundige oefeningen met het Eulergetal
Hier zijn twee voorbeelden van opgeloste wiskundige problemen met het Eulergetal:
1. Zoek de waarde van “e ix ” waarbij x een reëel getal is:
De identiteit van Euler vertelt ons dat e ix = cos(x) + i · sin(x). Als we de waarde van x kennen, kunnen we daarom de waarde van e ix berekenen met behulp van trigonometrische functies.
2. Bereken e^(x 2 ) voor een gegeven waarde van x:
We kunnen de Taylorreeks gebruiken om de waarde van e^(x 2 ) te berekenen. De Taylorreeks van e x is een oneindige uitbreiding die het mogelijk maakt om opeenvolgende benaderingen van de waarde van e x te berekenen, afhankelijk van de gebruikte term.

Als we in deze reeks x 2 vervangen door x, krijgen we de Taylorreeks voor e^(x 2 ).