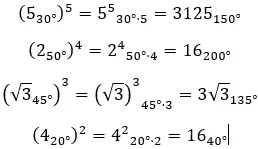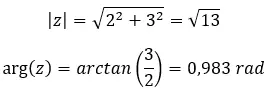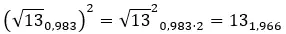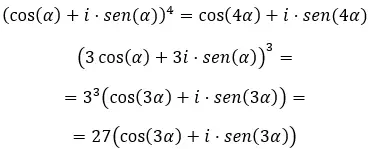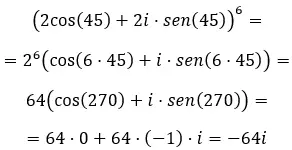Het oplossen van de machten van complexe getallen is vrij eenvoudig, als je de juiste methode kent. Daarom zullen we in dit artikel uitleggen hoe je complexe machten op drie manieren kunt oplossen: voor complexe getallen in binominale vorm, in polaire vorm en in trigonometrische vorm.
Hoe los je de macht van een complex getal op?
Zoals we in de inleiding al zeiden, kunnen zich bij het werken met complexe bevoegdheden drie situaties voordoen. De eerste en eenvoudigste is wanneer we het getal in polaire vorm krijgen. De tweede is wanneer we het getal in binominale vorm krijgen en de derde is wanneer we het getal in trigonometrische vorm krijgen.
Met andere woorden: bij het werken met complexen in polaire vorm kan de oefening sneller worden opgelost. Daarom wordt aanbevolen om het betreffende getal om te zetten in polaire vorm. Maar eigenlijk zijn alle methoden eenvoudig op te lossen . Dat gezegd hebbende, leggen we u uit hoe alle gevallen worden opgelost en bieden we u een oefening aan.
Machten van complexe getallen in polaire vorm
Als we complexe machten in polaire vorm willen oplossen, verhogen we eenvoudigweg de modulus naar any en vermenigvuldigen we het argument met n. Wiskundig uitgedrukt verkrijgen we de volgende formule:
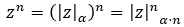
Hier zijn enkele voorbeelden, zodat u kunt proberen ze zelf op te lossen:
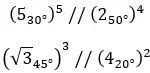
Machten van complexe getallen in binomiale vorm
Aan de andere kant, als we complexe machten in binominale vorm willen oplossen, kunnen we twee verschillende methoden gebruiken. De eerste gaat over het oplossen van de macht op een “algebraïsche” manier (oplossen alsof ik een variabele ben). En het tweede systeem is om de binomiale vorm naar polair om te zetten en vervolgens de procedure van daarvoor te volgen.
Als je niet weet hoe je van binomiale naar polaire vorm moet gaan, leggen we dat heel duidelijk uit in ons artikel over complexe getallen . Hoewel, nu zullen we het snel zien met een voorbeeld.
Probeer de volgende complexe macht op te lossen: (2 + 3i) 2 .
Machten van complexe getallen in trigonometrische vorm
Als we ten slotte complexe machten in trigonometrische vorm willen oplossen, moeten we de bekende formule van de Moivre gebruiken. Die als volgt geschreven is:
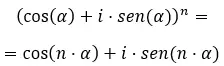
Als u deze formule kent, probeer dan de volgende oefeningen op te lossen: