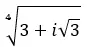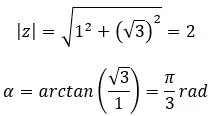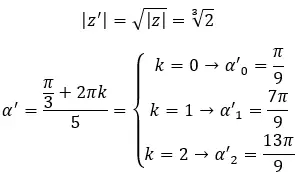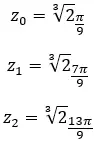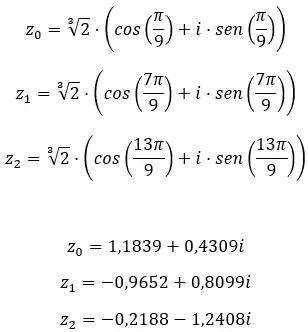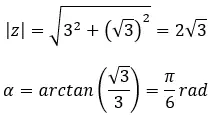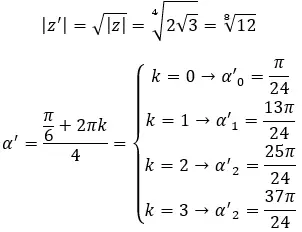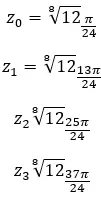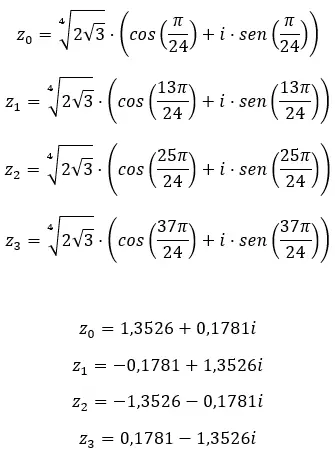Het berekenen van de wortels van complexe getallen is vrij eenvoudig. Als je de procedure eenmaal begrijpt, is het behoorlijk repetitief. Vervolgens leggen we het uit en geven we je een voorbeeld, zodat je het in echte oefeningen kunt leren toepassen.
nde wortels van complexe getallen
Het concept van de n-de wortel is gelijk aan het zeggen van de wortel van de orde n. Daarom wordt dezelfde methode gebruikt om de vierkantswortel en de vijfde wortel van een complex getal te berekenen. Afhankelijk van deze volgorde zal het aantal oplossingen uiteraard veranderen.
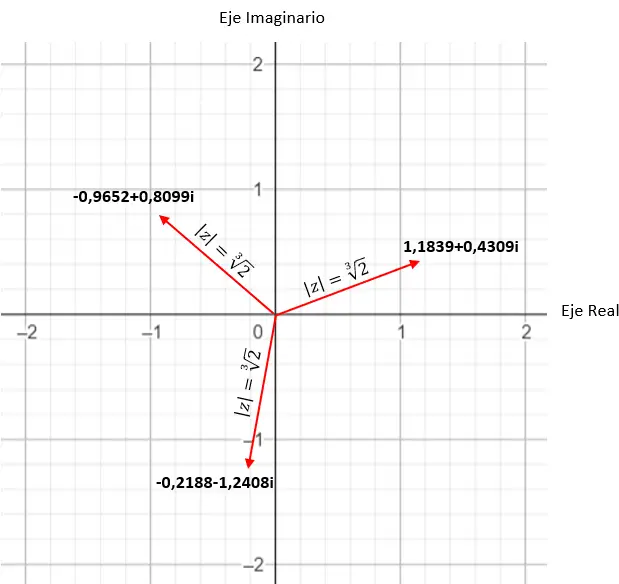
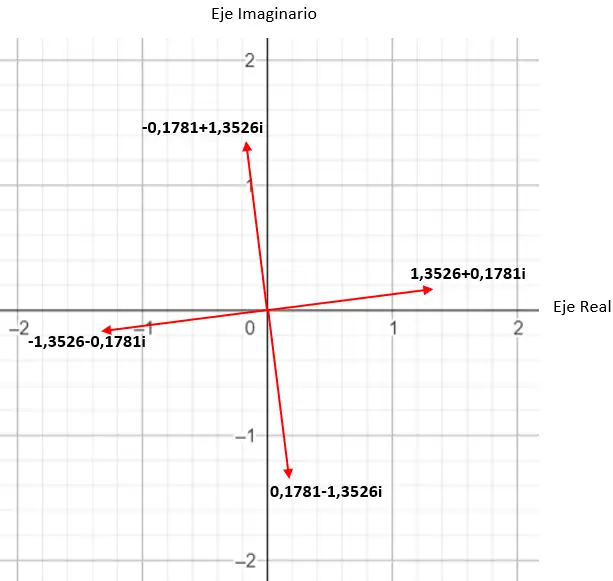
Als we bijvoorbeeld de vierde wortel van een complex berekenen, krijgen we vier verschillende oplossingen. En als we het in het complexe vlak uitdrukken, zien we dat er een regelmatige veelhoek met vier zijden ontstaat, gecentreerd op de oorsprong van het vlak. Dit is een zeer interessante eigenschap, die we later in detail zullen zien (in de voorbeeldensectie).
Nu we dit concept hebben verduidelijkt, zullen we zien hoe we de wortel van een complex getal in polaire vorm kunnen berekenen (het gebruik van deze notatie is het meest comfortabel voor het oplossen van een wortel). U hoeft eenvoudigweg de wortel van de modulus te berekenen en het argument uit te drukken in termen van n. Met andere woorden, de wortel van het volgende complexe getal (z):
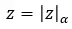
Deze bedragen om te berekenen:
- Module: De n-de wortel van de initiële module.
- Argument: Voeg 2πk in radialen of 360k in graden toe aan het argument en deel door n.
Wiskundig gezien gebruiken we de volgende twee formules om de module en het argument te berekenen:
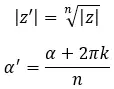
Waar, k = 0, 1, 2, …, n-1.
En daarom drukken we het resultaat als volgt uit:
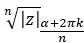
Voor alle duidelijkheid: de n oplossingen die we zullen verkrijgen door deze wortel op te lossen, zullen gevormd worden door dezelfde module en n verschillende argumenten.
Voorbeelden van het berekenen van n-de wortels van complexen
We zullen nu enkele voorbeelden zien van het berekenen van de n-de wortels van complexe getallen. We raden u aan de problemen zelf op te lossen en als u klaar bent, de oplossing te bekijken. Vergeet niet dat de methode hierboven wordt uitgelegd.
Zoek de derde wortel van het complexe getal: 1 + i √3 .
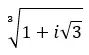
Zoek de vierde wortel van het complexe getal: 3+i √ 3 .