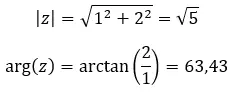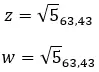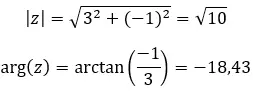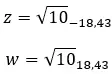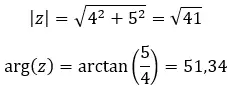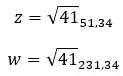In dit artikel bespreken we de eigenschappen van complexe getallen , wat handig kan zijn bij het oplossen van berekeningen en het vereenvoudigen van uitdrukkingen. Laten we meteen naar deze eigenschappen gaan.
Modulus en argument van een complex getal
De eerste eigenschap van een complex getal is de modulus en het argument van een complex getal. Het is heel eenvoudig te berekenen, omdat u slechts een paar formules hoeft toe te passen.
De formule om de module te berekenen:

De formule om het argument te berekenen:

Als het getal nu in polaire of trigonometrische vorm wordt uitgedrukt, is het niet nodig om berekeningen uit te voeren. Omdat in dezelfde expressie module en argument worden vermeld.
In de onderstaande afbeelding zie je de formule voor een getal in polaire vorm, waarbij |z| is de modulus en α is het argument.

En in deze andere afbeelding kun je de structuur zien van een getal, uitgedrukt in trigonometrische vorm, waarbij |z| is de modulus en α is het argument.

gelijke complexe getallen
Gelijke complexe getallen zijn getallen die modulus en argument delen. Dus uit deze twee waarden:

Deze zijn hetzelfde als aan de volgende eigenschap wordt voldaan.
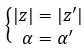
Aan de andere kant, als we beide getallen in binominale vorm hebben, kunnen we heel snel en eenvoudig controleren of het twee gelijke complexe getallen zijn. Er moet eenvoudigweg aan de volgende uitdrukking worden voldaan:
een + bi = een + bi
Laten we een voorbeeld bekijken en bepalen of de volgende twee complexe getallen gelijk zijn:
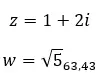
Complexe getallen vervoegen
Laten we nu verder gaan met een van de belangrijkste eigenschappen van complexe getallen, omdat weten hoe we de conjugaat van een complex moeten berekenen ons veel helpt bij het oplossen van complexe delingen en het maken van vereenvoudigingen.
Dus uit deze twee waarden:

We zeggen dat ze geconjugeerd zijn als ze een module delen en tegengestelde argumenten hebben. Het moet daarom worden ingevuld:
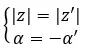
Aan de andere kant, als we beide getallen in binominale vorm hebben, kunnen we heel snel en gemakkelijk controleren of het twee complexe geconjugeerde getallen zijn. Er moet eenvoudigweg aan de volgende uitdrukking worden voldaan:
un + bi = un – bi
Laten we een voorbeeld bekijken en bepalen of de volgende twee complexe getallen geconjugeerd zijn:
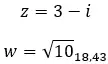
Tegenover complexe getallen
Vervolgens gaan we verder met het bekijken van de eigenschap van tegengestelde complexe getallen. Van deze twee waarden:

We kunnen zeggen dat ze tegengesteld zijn als ze dezelfde module hebben en hun argumenten 180 graden of π radialen verschillen:
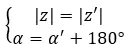
Aan de andere kant, als we beide getallen in binominale vorm hebben, kunnen we een nog snellere en eenvoudigere methode gebruiken om erachter te komen of het twee tegengestelde complexe getallen zijn. Er moet eenvoudigweg aan de volgende uitdrukking worden voldaan:
a + bi = -a – bi
Laten we een voorbeeld bekijken en bepalen of de volgende twee complexe getallen tegengesteld zijn:
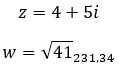
andere eigenschappen
Het is duidelijk dat deze getallenset andere eigenschappen heeft, zoals inverse complexe getallen en een paar andere die rechtstreeks verband houden met elementaire rekenkundige bewerkingen. Hoewel deze allemaal worden behandeld in andere artikelen, die u in de onderstaande lijst kunt zien.