Je hebt vast wel eens gehoord van de reeks denkbeeldige getallen of de denkbeeldige eenheid. Het is een wiskundig concept dat voortkomt uit de wiskundige behoefte om getallen uit te drukken die niet tot de reële getallen behoren.
Wat zijn denkbeeldige getallen?
Denkbeeldige getallen zijn getallen die, wanneer ze worden gekwadrateerd, een negatief getal opleveren. Daarom zijn dit waarden die gelijkwaardig zijn aan de vierkantswortel van een negatief getal. De denkbeeldige eenheid (het getal i) is bijvoorbeeld gelijk aan de vierkantswortel van -1.
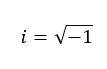
Deze getallen behoren niet tot de reële getallen, omdat in de reële verzameling negatieve wortels niet kunnen worden opgelost. Dit is waar het belang van de denkbeeldige setting ligt. Deze set is uitgevonden om met negatieve wortels om te kunnen gaan en om al die vergelijkingen en kwadratische problemen op te kunnen lossen die “geen oplossing hebben”, omdat ze ons een negatieve wortel geven.
Om verwarring te voorkomen is het belangrijk om onderscheid te maken tussen denkbeeldige getallen en complexe getallen . Complexen zijn getallen die zijn samengesteld uit een reëel getal en een denkbeeldig getal . Daarom zijn denkbeeldige beelden een subcategorie van complexen, die geen reëel deel hebben. In de volgende tabel kunt u de verschillen beter waarderen.
| complex getal | koninklijke partij | verbeelding deel | Beschrijving |
| 4+7i | 4 | 7i | Complex |
| 3 | 3 | 0 | puur koninklijk |
| 2i | 0 | 2i | Puur verbeelding |
Om de situering van deze digitale set af te ronden, kunnen we in de volgende afbeelding een structuur van alle sets visualiseren. Zoals we kunnen zien, omvatten complexe getallen alle soorten getallen . Deze kunnen op hun beurt worden onderverdeeld in reële getallen en pure denkbeeldige getallen (die we in dit artikel behandelen).

Voorbeelden van denkbeeldige getallen
Uit de denkbeeldige eenheid (i) kunnen we andere denkbeeldige getallen afleiden. U hoeft alleen maar de volgende formule toe te passen:
m = ri
Waar m een denkbeeldig getal is, is r een reëel getal en i de denkbeeldige eenheid. In de volgende afbeelding kun je zien hoe we verschillende denkbeelden uit negatieve wortels halen.
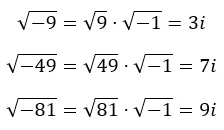
In feite kunnen we het extrapoleren naar de volgende uitdrukking:
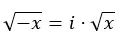
Eigenschappen van denkbeeldige getallen
Denkbeeldige getallen hebben een aantal zeer interessante eigenschappen . Over sommige hebben we het al gehad aan het begin van dit artikel, over andere niet:
- Denkbeelden behoren niet tot het geheel van realiteiten, omdat het getallen zijn die fysiek niet bestaan en niet kunnen worden weergegeven in onze realiteit.
- Dit zijn waarden die gelijkwaardig zijn aan negatieve wortels.
- Ze kunnen grafisch worden weergegeven op de denkbeeldige lijn.
- Denkbeeldige machten (dit is een concept dat we in de volgende sectie zullen uitleggen) zijn een grote hulp bij het vereenvoudigen van numerieke berekeningen met denkbeeldige waarden.
- De formule van Euler is een uitdrukking waarmee u denkbeeldige getallen aan reële getallen kunt koppelen.
Bewerkingen met denkbeeldige getallen
Nu je alle belangrijke kenmerken van denkbeeldige getallen kent, is het tijd om te leren hoe je bewerkingen ermee kunt oplossen. Om met denkbeeldige waarden te werken , moet je dezelfde stappen volgen die je volgt om met echte waarden te werken, behalve dat je rekening moet houden met één concept: denkbeeldige krachten.
verbeeldingskracht
Denkbeeldige getallen hebben een zeer interessante eigenschap die optreedt wanneer je de denkbeeldige eenheid met zichzelf vermenigvuldigt. Dat wil zeggen, dit gebeurt wanneer je krachten van denkbeeldige eenheid maakt. Als we de krachten opschrijven, zoals in de volgende lijst, kan een patroon worden ontdekt:
ik 0 = 1
Ik 1 = Ik
ik 2 = ik · ik = ( √ -1) · ( √ -1) = -1
ik 3 = ik 2 ik = (-1) ik = -i
ik 4 = ik 2 ik 2 = (-1) (-1) = 1
Als we dit concept kennen, wordt het voor ons veel gemakkelijker om bewerkingen met denkbeeldige getallen op te lossen, omdat we moeilijke bewerkingen kunnen vereenvoudigen en een beetje gemakkelijker kunnen maken. Het goede aan deze krachten is ook dat ze zich voor onbepaalde tijd herhalen. We kunnen dit zien als we nog een paar bevoegdheden toevoegen:
ik 5 = ik
ik 6 = -1
ik 7 = -ik
ik 8 = 1
enz.
En bij negatieve krachten gebeurt dit ook.
Rekenkundige bewerkingen met denkbeeldige getallen
Vervolgens geven we u een voorbeeld van elke eenvoudige rekenkundige bewerking, zodat u de denkbeeldige getalberekeningen opgelost kunt zien.
- Denkbeeldige getallen optellen: het is precies hetzelfde als het optellen van reële getallen, vergeet alleen niet de i toe te voegen.
4i + 3i = 7i
- Aftrekken van denkbeeldige getallen: Aftrekkingen worden ook op dezelfde manier opgelost als in de echte verzameling.
4i – 3i = ik
- Vermenigvuldiging van denkbeeldige getallen: in dit geval moeten we de denkbeeldige machten in gedachten houden die we eerder noemden.
3i 4i = 12 ik 2 = 12 (-1) = -12
- Deling van denkbeeldige getallen: bij dit soort delingen moeten we ook waakzaam zijn, voor het geval we een denkbeeldige kracht tegenkomen die ons in staat stelt de operatie te vereenvoudigen.
12i ÷ 4i = 3
Vergelijkingen met denkbeeldige getallen
Zoals we eerder zeiden, krijgen we bij het oplossen van vergelijkingen in de reële verzameling soms negatieve wortels en daarom hebben de vergelijkingen “geen oplossing” . Maar nu we de denkbeelden kennen, kunnen we deze vergelijkingen oplossen. Laten we een voorbeeld bekijken:
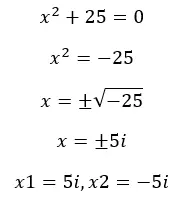
Waar worden denkbeeldige getallen voor gebruikt?
Denkbeeldige getallen komen voort uit de behoefte om waarden uit te kunnen drukken die buiten de reële verzameling liggen. Daarom lijkt het in eerste instantie misschien alsof ze niet veel nuttige toepassingen hebben. Maar de waarheid is dat het precies het tegenovergestelde is. Want als we ze combineren met de echte, krijgen we de complexe getallen.
En deze hebben vele toepassingen. Ze worden gebruikt om wisselstroom te bestuderen (omdat deze negatieve waarden heeft). Het gebruik ervan is ook zeer wijdverbreid op het gebied van golven (dat toepassingen heeft in de natuurkunde, telecommunicatie-elektronica en kwantummechanica). Naast vele andere toepassingen.
Bovendien komt het vaak voor dat wanneer je een kwadratische vergelijking oplost, de waarde je een negatieve wortel oplevert en je niet kunt opereren… Met verbeeldingen kun je ze oplossen . Concluderend kunnen we dus zeggen dat het een verzameling is die ons in staat stelt onze meer abstracte kennis uit te breiden.