De formule van Euler is een wiskundig concept dat twee elementaire concepten van de wiskunde met elkaar verbindt: complexe getallen en trigonometrie. Dit maakt het een van de belangrijkste conceptualisaties en met de meeste toepassingen in de hele wiskunde. In dit artikel zullen we zien hoe deze formule eruit ziet en welke toepassingen deze heeft.
Wat is de formule van Euler?
De formule van Euler is een fundamentele wiskundige vergelijking gebaseerd op het Euler-getal , dat complexe getallen relateert aan trigonometrie. Het werd in de 18e eeuw ontdekt door de Zwitserse wiskundige Leonhard Euler en wordt sindsdien op verschillende gebieden gebruikt, van natuurkunde tot informatica.
De formule van Euler wordt geschreven als e ix = cos(x) + i sin(x) , waarbij e de basis is van de natuurlijke logaritme, i dedenkbeeldige eenheid is (gedefinieerd als de vierkantswortel van -1), en x een reële eenheid is. nummer. Deze vergelijking specificeert dat het complexe getal e ix gelijk is aan de som van het reële getal cos(x) en het product van het denkbeeldige getal i door het reële getal sin(x).

Het belang van de formule van Euler ligt in het feit dat complexe getallen kunnen worden uitgedrukt in termen van reële getallen en trigonometrie, waardoor ze gemakkelijker te manipuleren en te berekenen zijn.
Bewijs van de formule van Euler
Het bewijs van de formule van Euler is gebaseerd op het gebruik van de Taylorreeks voor de exponentiële functie en de trigonometrische identiteit voor cosinus en sinus.
Eerst beschouwen we de Taylorreeks voor de exponentiële functie:

Vervolgens vervangen we x door ix in de bovenstaande vergelijking, waarbij i de denkbeeldige eenheid is (vierkantswortel van -1):
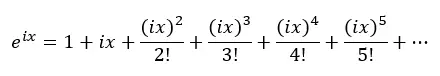
Dus passen we de machten van i toe en vervangen deze in de vorige vergelijking:
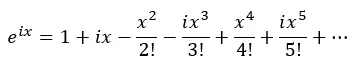
Nu groeperen we de reële termen en de termen met i:
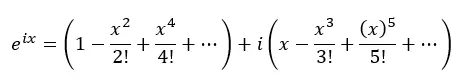
In feite is elk van de bovenstaande haakjes de Taylorreeks voor cosinus en sinus:
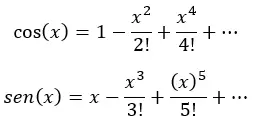
Ten slotte vereenvoudigen we (door elke uitdrukking tussen haakjes te vervangen door de cosinus en sinus van x) en verkrijgen we:

Voorbeeld van de formule van Euler
Nu je weet hoe deze wiskundige formule werkt, raden we je aan het volgende praktische voorbeeld op te lossen: Druk het complexe getal e 2i (in radialen) uit in binomiale vorm:
De belangrijkste toepassing van de formule van Euler is het omzetten van een complex getal uitgedrukt in exponentiële vorm in binomiale vorm. We zullen daarom de formule gebruiken : e ix = cos(x) + i sin(x)
e 2i = cos(2) + ik sin(2)
e2i = -0,416 + 0,909i
En we zouden het getal al in binominale vorm hebben. Van daaruit kunnen we de grafische weergave in het complexe vlak maken. Om dit te doen, is het noodzakelijk om te begrijpen dat een complex getal wordt weergegeven in het complexe vlak door als coördinaten het reële deel op de abscis (x-as) en het imaginaire deel op de ordinaat (y-as) te gebruiken.
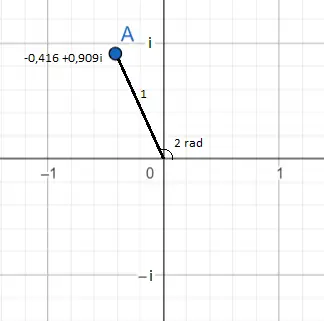
In de vorige afbeelding wordt het complexe getal e 2i weergegeven, dat gelijk is aan -0,416 + 0,909i. Dit kun je zien als een blauwgekleurde stip. De locatie in het vlak is vanuit twee hoeken te zien.
De eerste en meest voor de hand liggende is de weergave van het getal in binomiale vorm : -0,416 (op de abscis) en 0,909 (op de computer). En de tweede is in exponentiële vorm : de module van e 2i is gelijk aan 1, omdat dit het getal is dat vóór e staat (aangezien er geen getal vóór e staat, moeten we ons voorstellen dat er een 1 is) en in de exponent staat een 2, daarom is het argument of de hoek gelijk aan twee radialen.
Als je deze laatste paragraaf niet helemaal begrijpt , raden we je aan ons artikel over complexe getallen te lezen. Welnu, daar geven we een zeer diepgaande uitleg van de verschillende manieren om een complex getal en al zijn eigenschappen te schrijven.
Grafische weergave van de formule van Euler
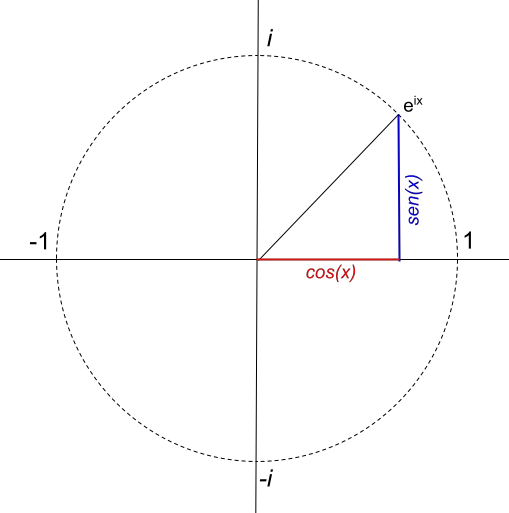
In het vorige voorbeeld kon je zien hoe de formule van Euler wordt toegepast en hoe deze grafisch wordt weergegeven in het complexe vlak. Maar als we iets verder gaan en proberen een functie weer te geven die equivalent is aan de formule van Euler, ontdekken we iets heel merkwaardigs: het genereert een cirkel met straal 1 :
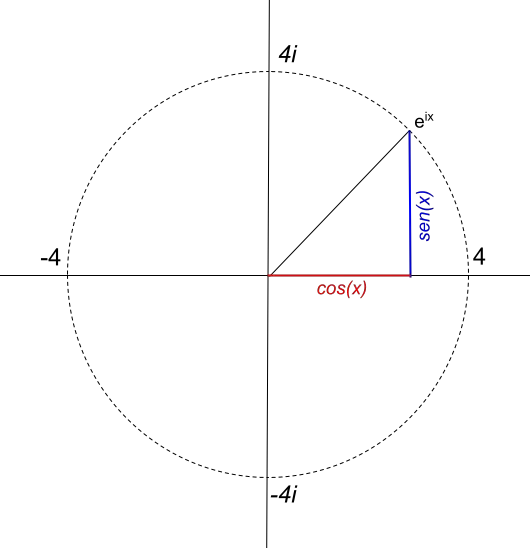
De straal van de cirkel hangt echter rechtstreeks af van de waarde van de module van het complexe getal. Als we bijvoorbeeld een cirkel met straal 4 willen weergeven, is de functie 4e ix . De functie 4e ix wordt dus als volgt weergegeven:
Terugkerend naar de cirkel met straal 1, als we besluiten e iπ (in radialen) weer te geven, moeten we eerst berekenen:
e πi = cos(π) + ik sin(π)
eπi = -1 + i 0
eπi = -1
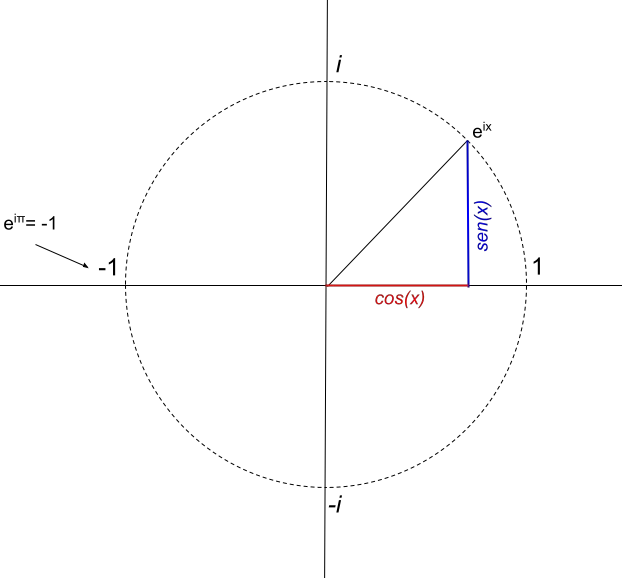
We verkrijgen e πi = -1, wat de beroemde Euler-identiteit is.
We leiden hieruit af dat het complexe getal e πi slechts één reëel deel heeft, dat gelijk is aan -1. Daarom zou de weergave ervan zodanig zijn dat:
Toepassingen van de formule van Euler
- Complexe getallen: de formule van Euler is een relatie tussen goniometrische functies en complexe getallen. Met deze formule kunnen we complexe getallen op verschillende manieren uitdrukken: binomiaal, exponentieel en polair.
- Taylorreeks: De formule van Euler wordt gebruikt om de functies van de Taylorreeks uit te breiden.
- Lineaire algebra: De formule van Euler wordt gebruikt bij matrixdiagonalisatie, een fundamentele techniek in lineaire algebra.
- Differentiaal- en integraalrekening: De formule van Euler wordt gebruikt bij het oplossen van differentiaalvergelijkingen, wat een relevante techniek is in de calculus.
Bovendien heeft het toepassingen in veel wiskundige theorieën en zelfs in concepten buiten het wiskundige domein, zoals natuurkundige stellingen.
conclusies
Zoals je in dit artikel hebt gezien, vindt de grootste toepassing van de formule van Euler plaats in complexe getallen : in de numerieke uitdrukking en in de weergave ervan. Het is waar dat dit enige toepassing heeft in de algebra, maar in essentie werk je met complexe getallen. Het is daarom belangrijk om ze vooral goed te begrijpen.
Dat gezegd hebbende, hopen we dat we u hebben geholpen dit concept beter te begrijpen. En als je vragen hebt of niet weet hoe je een oefening moet doen, aarzel dan niet om ons te schrijven in de reacties.