Het getal Pi is eenwiskundige constante die de relatie weergeeft tussen de omtrek van een cirkel en de diameter ervan. Het is een irrationeel getal. Met andere woorden, het is geen exacte breuk . Daarom kan het niet worden weergegeven als een eindig decimaal getal. De waarde van Pi is ongeveer 3,14159 en wordt weergegeven door de Griekse letter π.
Pi is een belangrijk getal in de wiskunde. Daarom heeft het vele toepassingen op verschillende gebieden. Het wordt bijvoorbeeld in de geometrie gebruikt om de oppervlakte te berekenen. Ook de omtrek van cirkels en andere ronde figuren. Aan de andere kant, in trigonometrie om hoeken en lengtes van bogen te berekenen. Ten slotte in techniek en natuurkunde om grootheden zoals volume en capaciteit te berekenen.
Pi-dag wordt elk jaar op 14 maart gevierd omdat de datum dicht bij de waarde van Pi (3,14) ligt. Deze datum wordt gevierd om Pi’s rol in de wiskunde te herdenken en de belangstelling voor deze fundamentele constante te bevorderen.
Wie heeft het getal Pi ontdekt?
Het getal Pi is al sinds de oudheid bekend en het was de Griekse wiskundige Archimedes (287-212 v.Chr.) die het nauwkeurig heeft beschreven . In feite gebruikte hij het om de oppervlakte en het volume van geometrische figuren te berekenen.
In de 18e eeuw bewees de Zwitserse wiskundige Johann Lambert dat Pi een irrationeel getal is. Later, in de 19e eeuw, legde de Duitse wiskundige Ferdinand von Lindemann uit dat Pi een transcendentaal getal is. Dat wil zeggen, het kan niet worden uitgedrukt als een exacte oplossing van een polynoomvergelijking met rationale coëfficiënten.
Door de geschiedenis heen hebben verschillende wiskundigen bijgedragen aan het begrip van het getal Pi en technieken ontwikkeld om het met grotere precisie te berekenen. Tegenwoordig is Pi nog steeds een van de belangrijkste en bekendste wiskundige constanten ter wereld en blijft het een onderwerp van studie in de wiskunde.
Waarom is het getal Pi oneindig?
De waarde van Pi is ongeveer 3,14159, maar in werkelijkheid is het een getal dat oneindig doorloopt na de komma. Dit betekent dat Pi een oneindig getal is en niet volledig kan worden weergegeven door een decimaal getal.
Hoewel de waarde van Pi oneindig is, kunnen in de praktijk geschatte waarden van Pi met grote precisie worden berekend. Inmiddels zijn miljoenen cijfers van Pi berekend en er is aangetoond dat Pi geen regelmatige patronen kent in de decimale cijfers. Al gebeurde dit via supercomputers omdat we niet zoveel getallen kunnen berekenen.
Welke methoden bestaan er om de geschatte waarde van het getal Pi te berekenen?
Er zijn verschillende praktische methoden om de waarde van Pi te berekenen. Vervolgens leggen we stap voor stap de drie methoden uit die het meest door wiskundigen worden gebruikt.
1. De methode van Archimedes
De Griekse wiskundige Archimedes gebruikte een geometrische methode om een geschatte waarde van Pi te berekenen. Om deze methode te gebruiken, volgt u de onderstaande stappen:
1. Teken een cirkel en trek een lijn door het middelpunt van de cirkel en snijd deze op twee tegenoverliggende punten, zoals hieronder weergegeven:
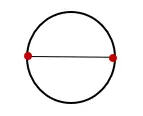
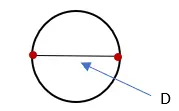
2. Meet de lengte van de lijn die de cirkel snijdt en label deze met “D”. Deze maat is de diameter van de cirkel.
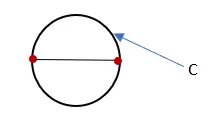
3. Meet de lengte van de lijn die de cirkel vormt en label deze met “C”. Deze maat is de omtrek van de cirkel.
4. Deel de omtrek van de cirkel (C) door de diameter van de cirkel (D). Het resultaat is een geschatte waarde van Pi.
Bijvoorbeeld: als de diameter van de cirkel 6 is en de omtrek 18, dan is de geschatte waarde van Pi 18 ÷ 6 = 3. Uiteraard is dit voorbeeld erg eenvoudig, maar als je het doet met waarden van een werkelijke omtrek , je zult zien dat de methode correct werkt.
We raden je zelfs aan het te proberen: meet een kopje of iets dat een ronde vorm heeft, en kijk of het voor jou werkt.
2. Monte Carlo-methode
De Monte Carlo-methode is een probabilistische methode die wordt gebruikt om geschatte waarden van Pi te berekenen. Om dit te doen, wordt een groot aantal punten willekeurig gegenereerd op een vlak en wordt het aantal punten geteld dat binnen een cirkel past die in een vierkant is ingeschreven. Het proces wordt als volgt toegepast:
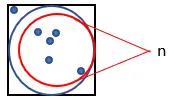
1. Teken een cirkel binnen een vierkant met zijde 1, zoals hieronder weergegeven:

2. Genereer willekeurig een groot aantal punten in het vierkant.
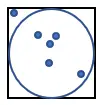
3. Tel het aantal punten dat in de cirkel past. Laten we deze grootheid “n” noemen.
4. Tel het totaal aantal gegenereerde punten. Noem deze hoeveelheid “m”.
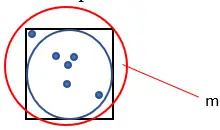
5. Bereken de geschatte waarde van Pi met behulp van de volgende formule: Pi = (4 · n) ÷ m.
Als er bijvoorbeeld 380 punten zijn gegenereerd en 300 passen in de cirkel, dan is de geschatte waarde van Pi (4 · 300) ÷ 380 = 3,16. Deze waarde lijkt veel op de eerste twee decimalen van Pi, maar net als bij de vorige methode geeft het gebruik van werkelijke metingen u een nog nauwkeurigere waarde .
3. Iteratiemethode
De iteratiemethode is een wiskundige methode die wordt gebruikt om geschatte waarden van Pi te berekenen. Deze methode maakt gebruik van een formule die de waarde van Pi impliceert en wordt iteratief toegepast om de nauwkeurigheid van de berekening te verbeteren. Hier zijn de stappen om deze methode te gebruiken:
- Kies een beginwaarde voor Pi. U kunt bijvoorbeeld de waarde 3 kiezen.
- Gebruik een formule met de waarde van Pi om een nieuwe geschatte waarde te berekenen. U kunt bijvoorbeeld de volgende formule gebruiken: Pi = (Pi + (4 ÷ Pi)) ÷ 2
- Vergelijk de nieuwe geschatte waarde met de oude waarde. Als het verschil tussen de twee klein genoeg is, heb je een nauwkeurig resultaat bereikt. Als het verschil nog steeds significant is, wijst u de nieuwe waarde toe aan Pi en herhaalt u het proces vanaf stap 2.
Als de initiële waarde van Pi bijvoorbeeld 3 is, zou de nieuwe geschatte waarde (3 + (4 ÷ 3)) ÷ 2 = 2,66666666 zijn. Maar aangezien het verschil tussen de twee niet erg klein is , kunt u het proces altijd meerdere keren herhalen voordat u een nauwkeurige waarde vindt.
Wat zijn de toepassingen van het getal Pi?
Pi is een belangrijk getal in de wiskunde en kent vele toepassingen op diverse terreinen. Tot de belangrijkste toepassingen van Pi behoren de volgende:
Geometrie
Pi wordt in de meetkunde gebruikt om de oppervlakte en omtrek van cirkels en andere cirkelvormige figuren te berekenen:
- Cirkels : Bereken de oppervlakte en de omtrek van de cirkels.
- Bollen : bepaal de oppervlakte en het volume van de bollen.
- Cilinders : Berekening van de oppervlakte en het volume van cilinders.
- Kegels – Wordt gebruikt om de oppervlakte en het volume van kegels te berekenen.
Trigonometrie
Het is handig in trigonometrie voor het berekenen van hoeken en booglengtes. Enkele van de toepassingen zijn:
- Hoeken : berekening van hoeken en booglengtes.
- Trigonometrische functies – Wordt gebruikt om de waarde van goniometrische functies voor bepaalde hoeken te berekenen.
- Circulaire trigonometrie : om de waarden van trigonometrische functies te berekenen voor hoeken van 360 graden.
Engineering
In de techniek wordt Pi gebruikt bij het berekenen van grootheden zoals volume en capaciteit. Enkele van de toepassingen zijn:
- Elektronica : bereken grootheden zoals weerstand en capaciteit.
- Elektriciteit : het wordt gebruikt om grootheden zoals stroom en elektrische energie te berekenen.
- Civiele techniek : bereken grootheden zoals de oppervlakte en het volume van constructies en constructie-elementen.
Fysiek
Het getal Pi (π) is een wiskundige constante die vele toepassingen kent in de natuurkunde. Hier zijn enkele voorbeelden van het gebruik van Pi in de natuurkunde:
- Golven – Wordt gebruikt om de frequentie en golflengte van golven te berekenen.
- Mechanica : In de mechanica is het handig voor het berekenen van arbeid en energie in roterende systemen.
- Elektromagnetisme : Bij elektromagnetisme kan het worden gebruikt om de energie te berekenen die is opgeslagen in een condensator en de inductie in een wikkeling.
- Kosmologie In de kosmologie wordt Pi gebruikt om de kromming van de ruimte-tijd en de uitdijing van het heelal te berekenen.
Welke toepassingen heeft het getal Pi in het echte leven?
Hier zijn enkele voorbeelden van hoe Pi in het dagelijks leven wordt gebruikt:
- Geometrie : om de oppervlakte van een ronde mat te definiëren of om de lengte van het meetlint te meten die nodig is om de omtrek van een ronde tafel te bedekken.
- Koken – bepalen hoeveel water of vloeistof er nodig is om een pan te vullen of hoeveel ingrediënten er in een ronde container passen.
- Astronomie : ken de afstand tussen de planeten en de sterren, de baan van de planeten en de positie van hemellichamen aan de hemel.
- Tuinieren : Weet hoeveel aarde of aarde nodig is om een ronde pot te vullen of om de hoeveelheid water te berekenen die nodig is om een plant in een ronde tuin water te geven.