Heb je je ooit afgevraagd hoe rationale getallen verschillen van andere getallen? In dit artikel zullen we rationale getallen diepgaand onderzoeken, inclusief hun unieke kenmerken en classificatie. Maak je klaar om het concept beter te begrijpen!
Wat zijn rationale getallen?
Rationele getallen (ℚ) zijn een subklasse van reële getallen die alle getallen omvat die als breuk kunnen worden uitgedrukt. Dit betekent dat rationale getallen de getallen zijn die kunnen worden geschreven als een verhouding van twee gehele getallen, a/b, waarbij b ≠ 0.
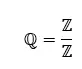
Rationele getallen kunnen ook worden uitgedrukt als herhaalde of eindige decimale getallen, omdat ze uit een reeks herhaalde cijfers bestaan. Enkele voorbeelden van rationale getallen zijn 1/2, 3/4, 10/3, 2/3 en π (pi).
Subsets van rationale waarden
Rationele getallen kunnen in twee subsets worden verdeeld:
- Gehele getallen , waaronder 0, alle natuurlijke getallen en alle negatieve getallen.
- Decimale getallen of breukgetallen , dit zijn allemaal waarden die waarden uitdrukken die worden gevormd door: een geheel getal en een decimaal deel, met dit laatste kunnen waarden kleiner dan één worden uitgedrukt.

Een andere subcategorie van de reeks reële getallen zijn irrationele getallen , die iets complexer zijn.
Voorbeelden van rationale getallen
Rationele getallen zijn getallen die kunnen worden uitgedrukt als een breuk, dat wil zeggen als een quotiënt van twee gehele getallen. Hier zijn enkele voorbeelden van rationale getallen:
-23
-4/5
-1/2
-7/9
Alle breuken die een geheel getal vertegenwoordigen, zijn even rationeel. Bijvoorbeeld:
-1/1
-2/2
-3/3
Eigenschappen van rationale getallen
Het belangrijkste kenmerk van rationale getallen is dat ze altijd een noemer hebben die niet nul is .
De tweede eigenschap van deze verzameling is dat elk rationeel getal kan worden weergegeven door een oneindig aantal equivalente breuken . Het rationale getal 3,5, dat gelijk is aan 7/2, kan bijvoorbeeld ook worden geschreven als 14/4, 28/8…, en een oneindig aantal andere breuken.
Rationele getallen voldoen ook aan de distributieve eigenschap . Dit betekent dat het vermenigvuldigen of delen van de ene breuk met de andere geen invloed heeft op het resultaat:
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (advertentie)/(bc)
Vertegenwoordiging van rationale getallen
Rationele getallen kunnen op verschillende manieren worden weergegeven, maar de meest voorkomende is als breuk . Een breuk bestaat uit twee getallen: de teller en de noemer.
De teller geeft aan hoeveel delen van het geheel in aanmerking worden genomen, terwijl de noemer aangeeft hoeveel gelijke delen het geheel bevat. Als een cake bijvoorbeeld in acht gelijke plakjes wordt verdeeld en drie van die plakjes worden gegeten, is de fractie die de hoeveelheid gegeten cake vertegenwoordigt 3/8.
Een andere manier om rationale getallen weer te geven is met decimalen . Decimalen zijn een verkorte manier om een breuk te schrijven waarbij de noemer een getal 10, 100, 1000, enz. is. Als u bijvoorbeeld 1/4 van een taart heeft, kan dit worden uitgedrukt als 0,25 (wat betekent “0 hele en 25/100”).
Hoewel we ze, als we ze grafisch willen weergeven, ook op de getallenlijn kunnen schrijven, waarin de volgorde van de getallen heel goed te zien is. Vervolgens laten we u een voorbeeld van deze regel zien:
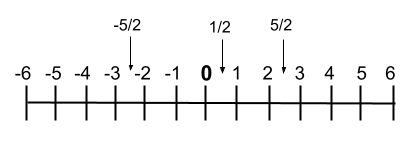
rationele operaties
De fundamentele bewerkingen van rationale getallen zijn dezelfde als die van gehele getallen: optellen, aftrekken, vermenigvuldigen en delen. Als je wilt leren hoe je dit soort bewerkingen kunt oplossen, raden we je aan ons artikel over bewerkingen met breuken te lezen.
Als u echter met rationale getallen met een decimale basis werkt, moet u de procedure voor het oplossen van bewerkingen volgen die u gebruikt bij het omgaan met decimale waarden .
Conclusie over de reeks rationale getallen
Na deze uitputtende uitleg kunnen we concluderen dat de reeks rationale getallen een van de belangrijkste is in de wiskunde. Het bevat alle getallen die als breuk kunnen worden weergegeven, waardoor we hoeveelheden heel nauwkeurig kunnen uitdrukken.