In dit artikel zullen we de concepten bekijken die nodig zijn om te begrijpen wat een volledige polynoom is. Daarnaast zullen we leren hoe het wordt gebruikt en waarom het zo’n belangrijk idee is voor het manipuleren en kwantificeren van polynomen. Hoewel het in de eerste plaats ten zeerste wordt aanbevolen om ons artikel over de polynoom te lezen.
Wat is een volledige polynoom?
Een volledige polynoom is een algebraïsche uitdrukking die bestaat uit een som van termen. Elke term wordt gevormd door een getal, een coëfficiënt genaamd, te vermenigvuldigen met een macht van x. De hoogste macht in de polynoom wordt de graad van de polynoom genoemd, en de laagste (x verhoogd tot nul) wordt de onafhankelijke term genoemd.
Vanaf hier definiëren we een volledige polynoom als een polynoom die termen van alle mogelijke graden omvat, tot aan de graad van de polynoom . Met andere woorden: als een polynoom graad 5 heeft, dan moet het termen van graad 5, 4, 3, 2, 1 en 0 bevatten. Met andere woorden: een volledige polynoom is een polynoom dat geen nultermen heeft (gelijk aan nul). ).
In de volgende afbeelding ziet u hiervan een voorbeeld. Zoals je kunt zien, heeft het een term voor elke exponent van x, van x tot de macht van vier (vier is de graad van de polynoom) tot x tot de macht nul, in de onafhankelijke term. Daarom voldoet dit polynoom aan de definitie van een volledig polynoom.
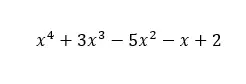
Aan de andere kant, als we een andere polynoom hebben zoals die in de volgende afbeelding, hebben we te maken met een onvolledige polynoom . Omdat er twee termen ontbreken, wordt die van x verhoogd naar twee en de onafhankelijke term. En uit de definitie van een volledige polynoom blijkt dat als er ook maar één term ontbreekt, de polynoom niet langer compleet is.
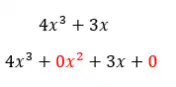
Voorbeelden van volledige polynomen
Nu u de definitie van de volledige polynoom kent, gaan we enkele voorbeelden uit de praktijk bekijken. We zullen beginnen met te kijken naar een volledige polynoom van graad 2, een andere van graad 4 en ten slotte één van graad 6. We zouden uiteraard voorbeelden kunnen geven van veel hogere graden, maar het idee is hetzelfde voor alle soorten polynomen.
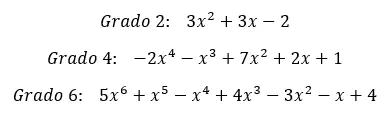
Met deze voorbeelden is de definitie van volledige polynomen heel duidelijk. Daarom kunnen we nu door naar het volgende niveau. In de volgende sectie zullen we de twee soorten volledige polynomen beschrijven die er bestaan, volgens de volgorde van de termen. Dit is iets wat veel studenten als vanzelfsprekend beschouwen, maar het is goed om het weer te zien.
Soorten complete polynomen
We kunnen volledige polynomen in twee typen indelen: geordende volledige polynomen en ongeordende of ongeordende volledige polynomen. De eerste worden gekenmerkt door een structuur waarvan de termen zijn geordend volgens de graden van x. Beginnend met de hoogste graad en eindigend met de term onafhankelijk.
Hoewel het een volledig ongeordend polynoom is, wordt het uitgedrukt met de termen in willekeurige volgorde . Daarom kun je de term met de grootste exponent naast de onafhankelijke term vinden. Maar deze manier om een polynoom uit te drukken is niet praktisch, dus raden wij u aan altijd geordende polynomen te gebruiken.
Vervolgens laten we u van elk type een voorbeeld zien, zodat u het verschil ten volle kunt waarderen.
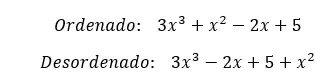
We hopen dat dit artikel je heeft geholpen het concept van volledige polynomen te begrijpen. Als u vragen heeft, kunt u deze achterlaten in de reacties.