Het getal nul is in veel culturen een belangrijk symbool en wordt op veel manieren gebruikt in de wiskunde en natuurwetenschappen. In dit artikel zullen we de eigenschappen van het getal 0, het gebruik ervan, de geschiedenis ervan en meer bekijken. Als u klaar bent met lezen, kent u de wiskundige toepassingen ervan, weet u hoe u het bij berekeningen moet gebruiken en kent u de oorsprong ervan.
Wat betekent het getal 0?
Het getal nul heeft niet altijd deel uitgemaakt van ons getallenstelsel. In feite is het concept ‘nul’ een relatief recente innovatie. Vroege getalsystemen konden het concept van ‘niets’ niet representeren.
De ontwikkeling van de rekenkunde en de noodzaak om hoeveelheden groter of kleiner uit te drukken dan met de beschikbare symbolen konden worden weergegeven, leidden echter tot de behoefte aan een symbool voor nul.
Het wordt eenvoudigweg gebruikt als symbool om de afwezigheid van kwantiteit weer te geven. Dit maakt het uiterst nuttig bij calculus, omdat het ons in staat stelt een getal aan te duiden dat geen waarde heeft.
De relatie met andere numerieke sets
Nul is op verschillende manieren gerelateerd aan andere getallen. Ten eerste kan nul als een ‘ neutraal ’ getal worden beschouwd, omdat het de waarde van enig ander getal niet beïnvloedt wanneer het wordt opgeteld of afgetrokken. 100 is bijvoorbeeld gelijk aan 98 + 2 + 0. Nul is ook het middelpunt van decimale nummering: 5 staat rechts van nul en -5 is links ervan.
Iets waar we op willen wijzen is dat het getal 0 niet is opgenomen in de verzameling natuurlijke getallen , hoewel het voor het gemak soms wel wordt opgenomen. Maar het is belangrijk om te weten dat het niet echt deel uitmaakt van deze set of de set negatieven, het is gewoon een geheel getal .
Eigenschappen van het getal nul
Nul kan worden gebruikt als wiskundige operator om de afwezigheid van een numerieke waarde aan te geven. Daarom wordt het over het algemeen een neutraal element genoemd. Bovendien wordt het weergegeven in het midden van de getallenlijn, dit komt omdat het de barrière vertegenwoordigt tussen negatieve en natuurlijke getallen.
In de wiskundige logica wordt het gebruikt om afwezigheid aan te duiden, dus als een logische uitspraak gelijk is aan nul, wordt er gezegd dat deze nul is. En in de informatica is het gebruik ervan essentieel, omdat het betekenis geeft aan binaire code , de taal die door alle wiskunde bij het programmeren wordt gebruikt.
Vertegenwoordiging van het getal nul
Zoals we eerder zeiden, wordt het getal 0 weergegeven in het midden van de getallenlijn . Deze waarde markeert inderdaad het verschil tussen negatieve getallen (kleiner dan nul) en positieve getallen (groter dan nul). In de onderstaande afbeelding ziet u een weergave van de getallenlijn met het getal nul precies in het midden:
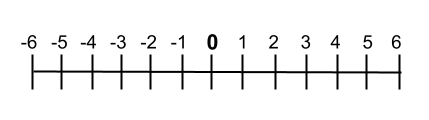
Het getal nul in wiskundige bewerkingen
Het getal nul 0 is een waarde die de afwezigheid van kwantiteit vertegenwoordigt. Als zodanig is het het symbool dat bij wiskundige bewerkingen wordt gebruikt om aan te geven dat er niets op te tellen of af te trekken valt. Hoewel het misschien een eenvoudig concept lijkt, is het omgaan met het getal nul een beetje ingewikkelder, bij vermenigvuldigen en delen.
Optellen en aftrekken is 0 een getal dat niets toevoegt, het verandert niets aan het resultaat. Terwijl het bij vermenigvuldigings- en delingsbewerkingen nogal wat doet. Als we bijvoorbeeld een getal met nul vermenigvuldigen, is het resultaat nul . Wat het getal ook is, het resultaat zal altijd 0 zijn.
Aan de andere kant, als je nul door een willekeurig getal deelt , krijg je 0 en als je de bewerking andersom uitvoert, is het resultaat oneindig . Tenzij je de bewerking 0 ÷ 0 uitvoert, wat dan onbepaaldheid genereert. Zoals u kunt zien, is delen door nul een iets complexere bewerking dan de vorige.
Het verhaal van nummer 0
Het getal nul is onafhankelijk in verschillende delen van de wereld uitgevonden. Sommige historici geloven dat het eerste gebruik van nul in India plaatsvond, terwijl anderen beweren dat dit in Babylon plaatsvond. Wat wel duidelijk is, is dat het getal nul een menselijke uitvinding is en geen inherente betekenis heeft.
De uitvinding van nul was een fundamentele stap in de ontwikkeling van de wiskunde en had een aanzienlijke impact op de manier waarop de wereld er vandaag de dag uitziet. Zonder nul zouden getallen en wiskundige bewerkingen heel anders zijn. Het is zelfs niet overdreven om te zeggen dat nul betekenis geeft aan de moderne calculus .
Het merkwaardige is dat Griekse wiskundigen het in de oudheid niet in hun berekeningen gebruikten. De Maya’s gebruikten het echter en het was de hindoeïstische wiskundige Brahmagupta die het in de 7e eeuw in Europa introduceerde.
Sindsdien is Zero heel belangrijk geweest voor de mensheid: het heeft de moderne technologie mogelijk gemaakt.
Momenteel heeft nul een brutaal belang in de wiskunde en de natuurwetenschappen. In de natuurkunde is het absolute nulpunt de laagst mogelijke temperatuur . In de scheikunde vertegenwoordigt nul op de pH-schaal een volledig zure oplossing. En bij computers is binaire nul de basis van alle getallen en numerieke berekeningen.
Bovendien is nul ook cruciaal in het dagelijks leven. Telefoonnummers en postadressen zouden niet hetzelfde zijn zonder de nul. En zonder nul zouden digitale klokken en rekenmachines natuurlijk niet kunnen bestaan. Nu je alles weet over het getal 0, wat denk je ervan?