Sinds de oudheid is de reeks natuurlijke getallen de basis geweest waarop veel takken van de wiskunde zijn gebouwd. Rekenkunde en meetkunde zijn bijvoorbeeld gebaseerd op deze getallen. Dat is de reden waarom we in dit korte artikel de definitie van natuurlijke getallen zullen zien en alle concepten die verband houden met deze verzameling.
Wat zijn de natuurlijke getallen?
Natuurlijke getallen zijn een reeks abstracte elementen die we gebruiken om objecten in de fysieke wereld te tellen en te ordenen . In de wiskunde wordt de reeks natuurlijke getallen doorgaans weergegeven door de letter ℕ. Deze bestaat uit alle positieve gehele getallen zonder decimalen en die niet fractioneel zijn: ℕ = {1, 2, 3, 4, 5, 6…}.
Met andere woorden, natuurlijke getallen zijn al die positieve gehele getallen die kunnen worden gebruikt om echte objecten te tellen. Op deze manier kunnen we zeggen dat het getal 1 een natuurlijk getal is, omdat we het kunnen gebruiken om echte objecten te tellen. We kunnen bijvoorbeeld een appel en twee peren hebben, wat in totaal drie vruchten zou opleveren.
In de volgende afbeelding laten we u een diagram zien dat alle getallensets samenvat, zodat u kunt zien waar de set ℕ zich bevindt. En welke relatie heeft het ten opzichte van de anderen, om het begrip natuurlijk getal beter te assimileren. Wij raden u aan, voordat u verder gaat met de uitleg, eerst de conceptmap goed te bekijken en te proberen deze te begrijpen.

Hoe weet je of een getal natuurlijk is of niet?
Zoals we al hebben gezegd, zijn de natuurlijke getallen de getallen die we gebruiken om te tellen en te ordenen. Om te weten of een waarde natuurlijk is of niet, moeten we het volgende in gedachten houden: een getal ℕ heeft geen negatief teken, het heeft geen decimalen, het heeft geen denkbeeldige eenheid en het is geen breuk. Vervolgens laten we u een lijst zien met de eerste 100 natuurlijke getallen:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 6 4, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75 , 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 en 100 .
Hoe worden natuurlijke getallen gelezen en geschreven?
De natuurlijke getallen volgen het decimale getalsysteem , dit betekent dat de waarden het getal tien als rekenkundige basis hebben. Alle getallen bestaan uit ten minste één van deze negen cijfers: 1, 2, 3, 4, 5, 6, 7, 8 en 9. En onthoud: een natuurlijk getal heeft in geen geval nooit een decimaalteken of een minteken. .
Voor zover het alle rekenkundige bewerkingen betreft, worden deze getallen geschreven volgens de wiskundige notatie . Als u twijfels heeft over een symbool of uitdrukking , raden wij u aan deze laatste link te openen en het artikel te lezen. Daar vindt u alle informatie met betrekking tot de wiskundige taal en alle notaties.
Kenmerken van natuurlijke getallen
Enkele van de belangrijkste kenmerken van natuurlijke getallen zijn:
- Het eerste natuurlijke getal is 1, aangezien 0 geen natuurlijk getal is.
- Ze worden gebruikt voor het meten, controleren en berekenen: ze kunnen worden gebruikt voor het meten van lengtes, gewichten, capaciteiten, enz.
- Ze kunnen met elkaar worden vergeleken: we kunnen zeggen welk getal groter of kleiner is dan een ander natuurlijk getal.
- Ze hebben een volgorde: natuurlijke getallen volgen een logische volgorde, beginnend bij 1 en eindigend bij oneindig.
- Twee natuurlijke personen kunnen niet dezelfde opvolger hebben, noch dezelfde voorganger.
- Alle natuurlijke getallen zijn gehele getallen, aangezien natuurlijke getallen positieve gehele getallen zijn en geen decimalen of breuken.
Ter afsluiting van dit gedeelte geven we u een reeks verduidelijkingen over deze verzameling die vaak twijfels oproepen bij studenten: het getal nul is geen natuurlijk getal, natuurlijke getallen zijn gehele getallen, natuurlijke getallen kunnen geen negatieve getallen zijn, natuurlijke getallen hebben geen decimalen. plaatsen, en natuurlijke getallen zijn oneindig.
Vertegenwoordiging van natuurlijke getallen
De verzameling natuurlijke getallen , ook wel ℕ genoemd, wordt gevormd door de positieve gehele getallen: 1, 2, 3, 4… enzovoort. Deze set wordt weergegeven door de volgende notatie: ℕ = {1, 2, 3, 4, 5…}. Ze kunnen echter ook grafischer worden weergegeven, door ze op de getallenlijn te plaatsen.
Deze tweede methode omvat het tekenen van een rechte horizontale lijn en het op een ordelijke manier schrijven van de waarden van de natuurlijke getallen langs de lijn. Je kunt dus gemakkelijk de volgorde van de set visualiseren. Dit systeem is erg goed voor degenen die deze numerieke set leren. In de volgende afbeelding kunt u zien hoe de rij-indeling eruit zou zien.
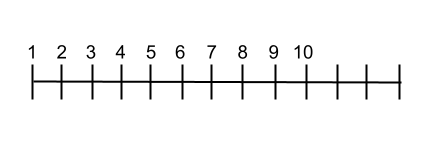
Bewerkingen met natuurlijke getallen
Nu je alle kenmerken en eigenschappen van de verzameling ℕ kent, is het tijd om ze toe te passen op rekenkundige bewerkingen , die de belangrijkste toepassing van deze getallen vormen. Vervolgens zullen we de vier basisbewerkingen (optellen, aftrekken, vermenigvuldigen en delen) in detail uitleggen.
Als we natuurlijke waarden optellen, krijgen we nog een getal ℕ: 3 + 6 = 9 . Maar als we natuurlijke getallen aftrekken, kan het resultaat een positief of negatief getal zijn. Deze laatste behoren niet tot de verzameling waar we het over hebben, dus alleen aftrekkingen die een positief resultaat hebben, maken deel uit van de verzameling ℕ: 4 – 2 = 2 .
Het geval van vermenigvuldiging tussen natuurlijke getallen is hetzelfde als dat van optellen, aangezien ze alleen tot een positief getal kunnen leiden. Als we bijvoorbeeld 3 en 8 willen vermenigvuldigen, levert dit ons 3 · 8 = 24 op. Maar als we de getallen in de verzameling ℕ verdelen, kunnen we in bepaalde gevallen een decimaal getal verkrijgen. In deze situatie maakt het resultaat geen deel uit van het natuurlijke geheel.
Daarom zijn in de verzameling natuurlijke getallen alleen optellen en vermenigvuldigen gedefinieerd. Deze twee bewerkingen controleren de commutatieve en associatieve eigenschappen. Als de begingetallen natuurlijk zijn, resulteren ze daarom altijd in een natuurlijk getal. Op deze manier zijn het bewerkingen die altijd de eigenschappen van de verzameling ℕ respecteren.
Toepassingen van natuurlijke getallen
Natuurlijke getallen worden vaak gebruikt in het dagelijks leven . Ze kunnen bijvoorbeeld worden gebruikt om de lengte van een tafel te meten of de tijd die iemand nodig heeft om naar een winkel te lopen. Ze kunnen ook worden gebruikt om wiskundige berekeningen uit te voeren, zoals optellen of aftrekken. Ook kunnen gehele getallen worden gebruikt om de positie van objecten in een ruimte te bepalen, zoals het plaatsen van boeken op een plank.