Wiskundige notatie is een manier om ideeën en berekeningen over te brengen door het gebruik van symbolen. Hoewel het op het eerste gezicht misschien verwarrend lijkt, zul je het met een beetje oefening gemakkelijk kunnen interpreteren. In dit artikel laten we u de betekenis zien van alle symbolen die in deze notatie worden gebruikt, en enkele voorbeelden van hoe u ze kunt toepassen.
Wat is wiskundige notatie?
Wiskundige notatie is een manier om waarden en uitdrukkingen te schrijven die in de wiskunde worden gebruikt. Met deze techniek kunnen wiskundigen ideeën beknopt en nauwkeurig formuleren. Wiskundige notatie zorgt er ook voor dat degenen die wiskunde beoefenen of studeren, concepten beter kunnen begrijpen.
De taal van de wiskunde mag niet worden verward met wetenschappelijke notatie, een manier om numerieke waarden te schrijven. Ondertussen is wiskundige notatie meer een reeks symbolen waarmee je complexe uitdrukkingen kunt schrijven, net als een taal. Op dit onderwerp komen we later uitgebreider terug.
Hoe wiskundige notatie lezen?
Het leren interpreteren van wiskundige notatie is gemakkelijker dan het lijkt. U hoeft alleen maar de betekenis van elk symbool te leren en als u dat eenmaal doet, kunt u alles lezen dat in wiskundige notatie is geschreven. Zo simpel is het, al vergt het uiteraard oefening en veel studietijd.
Wiskundige uitdrukkingen zijn erg logisch en volgen altijd patronen. Daarom hoeft u alleen maar de regels uit uw hoofd te leren, waarna u weet hoe u ze naar elke situatie kunt extrapoleren. We kunnen zelfs zeer complexe berekeningen beschrijven, dit is de magie van de wiskundige taal, waardoor zeer uitgebreide boodschappen op een methodische manier kunnen worden gecommuniceerd.
Componenten van wiskundige notatie
Wiskundige notatie bestaat uit een reeks symbolen die getallen, bewerkingen en de relaties daartussen vertegenwoordigen. Deze symbolen lijken in eerste instantie misschien ingewikkeld, maar met een beetje oefening en begrip zou het interpreteren van de wiskundige notatie kinderspel moeten worden.
Vervolgens zullen we in detail de vier soorten elementen uitleggen die in de wiskundige taal voorkomen. Beginnend met de meest basale en eindigend met de meest complexe en abstracte. En zodra de theoretische uitleg klaar is, zullen we het hebben over de soorten numerieke notaties die er bestaan.
Getallen en getallensets
Allereerst moeten we wiskundige getallen definiëren, het is een wiskundig concept dat een hoeveelheid aanduidt die verband houdt met een eenheid. We kunnen elke numerieke waarde beschrijven door het decimale nummeringssysteem te volgen en de volgende symbolen te combineren: 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9.
Als we getallen ordenen op basis van verschillende eigenschappen, krijgen we verschillende categorieën getallen, de zogenaamde getallensets. En deze groepen waarden hebben ook hun eigen symbolen die ze aanduiden. In de volgende lijst presenteren we ze allemaal met de naam van de overeenkomstige groep:
- ℙ: priemgetallen
- ℕ: natuurlijke getallen
- ℤ: Heel
- ℚ: rationale getallen
- ℝ: Reële cijfers
- 𝕀:denkbeeldige getallen
- ℂ: complexe getallen
- ℍ: quaternionen
Deze symbolen worden over het algemeen gebruikt in onze berekeningen om een breed scala aan getallen in één keer te bepalen. Als we bijvoorbeeld een expressie hebben die dienovereenkomstig veel waarden accepteert, in plaats van de getallen één voor één te schrijven, zal het voor ons gemakkelijker zijn om deze waarden op te geven via het symbool dat overeenkomt met hun numerieke groep .
Operatoren en kwantificatoren
Nu we getallen hebben besproken, die de essentie van de wiskunde vormen, moeten we het hebben over operatoren en kwantificatoren . De eerste zijn al die symbolen waarmee we een bewerking kunnen weergeven: optellen (+), aftrekken (-), vermenigvuldigen (x of ·), delen (÷), onder andere.
We hebben echter ook twee andere soorten operators, namelijk logische operators en relationele operators. De eerste drukt conjunctie, disjunctie en ontkenning uit. Ze helpen ons logische bewerkingen voor te stellen, die, in tegenstelling tot rekenkundige bewerkingen, niet met getallen werken, maar met wiskundige proposities.
Terwijl de tweede ons in staat stelt equivalenties en relaties tussen waarden of wiskundige uitdrukkingen vast te stellen . Deze symbolen kunnen worden gebruikt bij rekenkundige berekeningen (om getallen te ordenen), maar ze zijn belangrijker in de algebra, als we variabelen hebben (meer hierover in twee secties).
In de volgende lijst vindt u de definitie van alle operatoren die we tot nu toe hebben besproken:
| Symbool | Definitie | Vriendelijk |
| + | Toevoeging | rekenkundige operator |
| – | Aftrekken | rekenkundige operator |
| X, *, · | Vermenigvuldiging | rekenkundige operator |
| ÷ | Divisie | rekenkundige operator |
| x² | machtiging | rekenkundige operator |
| √ | borg | rekenkundige operator |
| EN | Voegwoord | logische exploitant |
| OF | Disjunctie | logische exploitant |
| NEE | Ontkenning | logische exploitant |
| = | Gelijk aan | relatie operator |
| > | Groter dan | relatie operator |
| < | Kleiner dan | relatie operator |
| >= | Beter dan of gelijk | relatie operator |
| <= | minder dan of gelijk aan | relatie operator |
| ≠ | is niet gelijk aan | relatie operator |
| ≡ | Precies dezelfde | relatie operator |
| ≈ | bijna gelijk | relatie operator |
| ≃ | Gelijk aan | relatie operator |
| ∝ | Proportioneel | relatie operator |
Hoewel er ook vijf andere logische operatoren zijn die worden gebruikt om wiskundige logica vanuit de verzamelingenleer te verklaren. Dat is een tak die vaste logica toepast, die wordt gebruikt in berekeningen, geometrie, statistieken… Vervolgens laten we u de symbolen zien die worden gebruikt en hun definitie.
| Symbool | Definitie |
| x ∈ EEN | x is van A |
| x ∉ EEN | x behoort niet tot A |
| ∪ | unie |
| ∩ | Kruispunt |
| ⊂ | Inclusie |
Wat kwantificatoren betreft, kunnen we deze definiëren als symbolen die het aantal elementen van een set aangeven dat aan een bepaalde voorwaarde voldoet (equivalentie, volgorde, lidmaatschap, enz.). Er is een grote verscheidenheid aan operators, maar een van de meest gebruikte kunnen we benadrukken:
| Symbool | Definitie | vriendelijk |
| ∀x | voor alle x | kwantificeren |
| ∃x | Er is minstens één x | kwantificeren |
| ∄x | er is geen x | kwantificeren |
| ∃!x | Er is maar één x | kwantificeren |
| | | Zoals | kwantificeren |
| ∴ | DUS | kwantificeren |
Wiskundige uitdrukkingen en hun relaties
Met de symbolen die we tot nu toe hebben behandeld, kun je veel wiskunde begrijpen, maar we hebben hun toepassingen of relaties in complexe uitdrukkingen, zoals gecombineerde bewerkingen of algebraïsche berekeningen, nog niet uitgelegd. Bovendien zijn er nog steeds relatiesymbolen om te bespreken. Dit zijn degenen die we in deze sectie zullen zien.
Te beginnen met de groeperingssymbolen: dit zijn haakjes, vierkante haakjes en accolades. Deze elementen zijn essentieel bij de aanduiding van complexe formules. De belangrijkste functie ervan is om prioriteit te geven aan bepaalde berekeningen, binnen een globale uitdrukking. En er zijn verschillende prioriteitsniveaus tussen de drie typen. In deze uitdrukking zie je de schrijfvolgorde 3 {[2 + (3 – 2) · 2] – 4}.
| symbolen | Definitie | Prioriteit |
| “(“En”)” | Haakje | Maximale prioriteit |
| “[“En”]” | Beugels | tweede prioriteit |
| “{” En “}” | Sleutels | derde prioriteit |
En om deze categorie af te ronden, zullen we het hebben over sommaties (Σ) en producten (∏) , dit zijn elementen waarmee we herhaalde optellingen en vermenigvuldigingen kunnen beschrijven. De optelling komt neer op het zeggen van: “som van Xi, waarbij i de waarden van 1 naar an neemt”. En het product is hetzelfde, maar in plaats van op te tellen, vermenigvuldigen we.
algebraïsche analyse
Het eerste dat we over algebraïsche symbolen moeten bespreken, zijn variabelen, die worden weergegeven door de letters van het alfabet. Hun functie is het imiteren van een getal , maar ze hebben geen vaste waarde zoalswiskundige constanten , dus ze kunnen nieuwe waarden aannemen. Dit geldt voor vergelijkingen, limieten, afgeleiden, integralen, matrices…
Ten slotte willen we het hebben over de representaties van al deze algebraïsche bewerkingen waar we het zojuist over hadden in de laatste paragraaf. Sindsdien vormen ze de basis van de algebra en moet je weten wat hun symboliek is. Vervolgens laten we u een tabel zien met de verschillende symbolen en een korte definitie:
| Symbool | Definitie |
| lim x → b | Limiet (wanneer x neigt naar b) |
| y ‘, ƒ’ (x), dy / dx | derivaat |
| ∫ | Compleet |
| Naar mxn | Matrix van MXN-afmetingen |
Conclusie over de symbolen van wiskundige taal
Tot nu toe heb je alle belangrijke symbolen gezien die in de wiskunde aan bod komen, er valt uiteraard nog meer te bespreken. Maar deze zijn specifieker voor elke subcategorie van de wiskunde: meetkunde, statistiek, algebra… We sluiten dit onderwerp daarom af en praten over numerieke notaties.
Soorten numerieke notaties
In deze sectie zullen we alle manieren zien om wiskundige getallen uit te drukken, omdat er verschillende notaties zijn om dit te doen. In het begin noemden we hierboven het decimale getalsysteem, dat het meest wordt gebruikt door wiskundigen. Vervolgens zullen we het in meer detail uitleggen en andere soorten wiskundige notaties laten zien:
decimale notatie
Het decimale getalsysteem is een positioneel getalsysteem (systeem waarin de positie van elk cijfer de waarde ervan bepaalt) en is gebaseerd op de veelvouden en subveelvouden van het getal 10. Aangezien tien het getal is dat als numerieke basis wordt gebruikt. Daarom zijn de tien cijfersymbolen die we zullen gebruiken: 1, 2, 3, 4, 5, 6, 7, 8, 9 en 0.
De waarde van deze getallen wordt bepaald op basis van de som van de cijfers vermenigvuldigd met de machten in het grondtal tien, vastgesteld op basis van de positie . En het is heel belangrijk dat u onthoudt dat u, als u een getal kleiner dan één wilt schrijven, de komma moet gebruiken. Hieronder ziet u een voorbeeld:
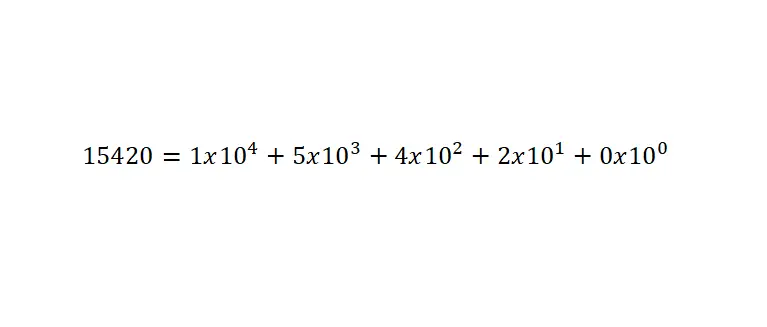
Wetenschappelijke notatie
Exponentiële vormnotatie of wetenschappelijke notatie is duidelijk een van de meest gebruikte schrijfwijzen in wetenschap en technologie. Hierdoor kunnen we op een eenvoudige manier zeer grote en zeer kleine getallen uitdrukken. Om de definitie van wetenschappelijke notatie te begrijpen, zullen we uitleggen hoe je een geheel getal aan deze notatie kunt doorgeven:
- Verplaats de komma: je moet de komma zo vaak als nodig verplaatsen totdat je het eerste cijfer bereikt (naar links als je een heel groot getal hebt en naar rechts als je een heel klein getal hebt).
- Bepaal de basis: schrijf dit laatste getal vermenigvuldigd met tien, dus naast de waarde die je hebt verkregen door de komma naar één kant te verplaatsen, moet je een vermenigvuldiging met tien schrijven: “x 10”.
- Voeg een exponent toe: met een waarde die gelijk is aan het aantal keren dat u de komma hebt verplaatst. Bij grote getallen laat u de exponent als positief staan, maar bij kleine getallen moet u deze met een negatief teken schrijven.
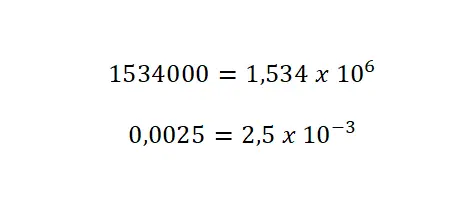
hexadecimale notatie
Het hexadecimale systeem is gebaseerd op 16, wat betekent dat het zestien verschillende symbolen gebruikt: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E en F. Zo goed als je kunt Zie je, dit nummeringssysteem bestaat uit de cijfers van het decimale systeem en zes letters. Deze notatie wordt over het algemeen vooral gebruikt in IT en alles wat met IT te maken heeft.
Het is belangrijk om te verduidelijken dat, aangezien het symbolen gemeen heeft met andere soorten notatie, we altijd moeten aangeven dat het in hexadecimaal is geschreven door middel van een haakje en de index 16 . In het volgende voorbeeld zie je aan de hand van een heel duidelijk voorbeeld de conversie van een hexadecimaal getal naar decimale notatie:
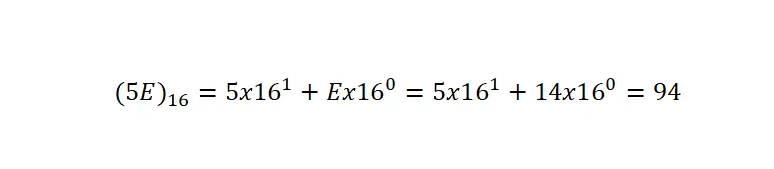
Om een hexadecimaal getal naar een decimale uitdrukking te converteren, moeten we het getal opsplitsen in basisvermenigvuldigingen, zoals we deden bij de decimale notatie, maar waarbij we de grondtal veranderden in 16 . Vervolgens vermenigvuldigen we elk cijfer met zestien, verhoogd tot de positie die dat specifieke cijfer inneemt min één.
octale notatie
Het laatste systeem waar we het over zullen hebben is de octale notatie , die een grondtal van 8 heeft. Dit betekent dat er slechts acht symbolen of cijfers worden gebruikt: 0, 1, 2, 3, 4, 5, 6 en 7. wordt het minst gebruikt nummeringssysteem van alle degenen die we hebben uitgelegd. Opgemerkt moet worden dat conversies van deze notatie worden uitgevoerd volgens dezelfde procedure als de vorige.
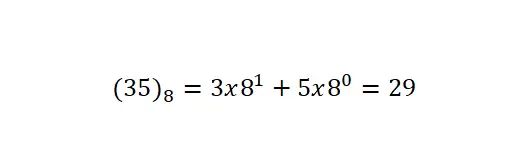
nieuwe notatie
Ten slotte kunnen we het hebben over het Romeinse cijfersysteem , dat tegenwoordig niet veel wordt gebruikt, maar in het verleden erg belangrijk was op het gebied van de wiskunde. Omdat het een van de notaties was die de wiskunde tot leven bracht.
Je schrijfwijze is beperkt tot 7 symbolen: I (1), V (5), X (10), L (50), C (100), D (500) en M (1000). En door deze letters te combineren, worden alle cijfers geschreven. Als je wilt weten hoe ze samen tot andere grotere aantallen leiden, raden we je aan ons artikel over hen te lezen, toegankelijk via de laatste link.
Hoe kan ik de leesprestaties in wiskundige notatie verbeteren?
Er zijn verschillende manieren om de prestaties bij het lezen van wiskundige notatie te verbeteren . Eén manier is om de symbolen en cijfers hardop voor te lezen. Een andere manier is om vertrouwd te raken met de symbolen en hun betekenis. Je kunt ook oefenen met het lezen van wiskundige notatie met behulp van oefeningen en problemen.
We hopen dat we u met deze gids hebben geholpen. Als u vragen heeft, aarzel dan niet om deze in de opmerkingen te stellen. Of als je graag een bijdrage wilt leveren over het onderwerp, dan hopen we dat ook in de reacties te zien. Dat gezegd hebbende, laten we een artikel achter over hoe je wiskunde kunt leren , voor het geval je verder wilt lezen.