Een onherleidbare breuk is een breuk die niet verder kan worden vereenvoudigd en heeft dus geen kleinere equivalente breuken . Met andere woorden: de ggf van de teller en de noemer van een onherleidbare breuk is gelijk aan 1, omdat ze geen andere gemeenschappelijke delers hebben. De uitdrukking “5/8” kan bijvoorbeeld niet langer worden gereduceerd, dus zeggen we dat deze in de eenvoudigste vorm is of dat deze onherleidbaar is.
Onherleidbare breukcalculator
Voordat we verder gaan met de theorie, willen we je een rekenmachine laten zien, waarmee je de onherleidbare fractie van elk gemengd getal kunt berekenen. Het enige wat u hoeft te doen is de waarden van de teller en de noemer in te voeren en op “Breuk vereenvoudigen” te klikken, u krijgt dan de gereduceerde vorm in het resultatenvak. We raden u aan deze tool te gebruiken om elke breuk onmiddellijk te vereenvoudigen of zelfs uw breukoefeningen te corrigeren.
Wat is een onherleidbare breuk en hoe wordt deze berekend?
Zoals we in het begin al hebben uitgelegd, is een onherleidbare breuk een breuk die niet verder kan worden vereenvoudigd, dus het is een onmiddellijke breuk . Als je dit soort breuken wilt vinden, zul je de vereenvoudiging van breuken moeten gebruiken, op deze manier zul je een gelijkwaardige breuk vinden die onherleidbaar is ten opzichte van de initiële breuk. In deze laatste link vindt u een gedetailleerde handleiding over het vereenvoudigen van breuken, hoewel we in de volgende lijst de stappen beknopt uitleggen:
- Gemeenschappelijke factoren vinden: Om te beginnen moet u de grootste gemene deler van de teller en de noemer vinden. Op deze manier krijgt u een getal waarmee u beide waarden kunt verlagen met behoud van de gelijkwaardigheid.
- Deel de reduceerbare breuk door de gcf: Zodra je de gcf hebt, moet je de teller en de noemer delen door deze gemeenschappelijke deler. Dit geeft je een eenvoudiger (of kleinere) equivalente teller en noemer.
Je kunt ook andere methoden gebruiken om onherleidbare breuken te vinden. Deze worden uitgelegd in ons artikel over het vereenvoudigen van breuken. Hoewel je met deze methodologie die we je hebben uitgelegd, elke gewenste fractie heel gemakkelijk en snel kunt verminderen .
Voorbeeld van reduceerbare breuken en onherleidbare breuken
In de volgende afbeelding vind je vier voorbeelden van reduceerbare breuken en nog vier van onherleidbare breuken. We raden u aan om elk van de breuken te vereenvoudigen, zodat u het verschil tussen de twee soorten breuken duidelijk zult begrijpen.
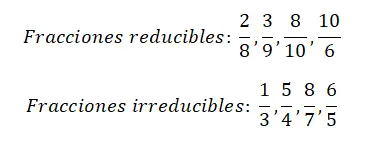
Voorbeeld van het berekenen van een irreducibele breuk
Hier laten we u stap voor stap zien hoe u een breuk op twee manieren kunt vereenvoudigen . De eerste toont de volledige procedure die we in de vorige sectie hebben uitgelegd. En de tweede toont een iets ander systeem, waarbij de teller en de noemer door dezelfde waarde worden gedeeld, beginnend met de kleinste delers (1 niet meegerekend) en vervolgens opwerkend. Als u echter denkt dat het tweede systeem te ingewikkeld is, kunt u het negeren.
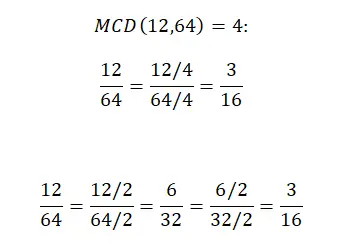
Onherleidbare fractie van een decimaal getal
De onherleidbare breuk die uit een decimaal getal wordt verkregen, wordt een genererende breuk genoemd. Het is belangrijk op te merken dat het op verschillende manieren wordt berekend, afhankelijk van het type decimaal waarmee we te maken hebben (exact, puur periodiek of gemengd periodiek). Het volgende voorbeeld laat dit wiskundige concept duidelijk zien: 5/7 = 0,7142857... Zoals je kunt zien, is vijf septiem de onherleidbare breuk die overeenkomt met het decimale getal 0,7142857...
Hoe weet je of een breuk onherleidbaar is?
Om erachter te komen of een breuk reduceerbaar of irreducibel is, kun je twee methoden volgen. De eerste is om de grootste gemene deler van de teller en de noemer te berekenen. Als deze waarde verschilt van één, betekent dit dat het een reduceerbare breuk is. En als je er één krijgt, weet je dat de breuk onherleidbaar zal zijn. Ten tweede kun je de rekenmachine voor onherleidbare breuken gebruiken die we je in het begin hebben laten zien om dit soort controles uit te voeren.
Opgeloste oefeningen over onherleidbare breuken
Nu je de theorie hebt gelezen, raden we je aan deze problemen op te lossen , zodat je kunt oefenen met het berekenen van onherleidbare breuken. Als u bovendien uw begrip van gemengde getallen wilt verbeteren, raden we u aan deze breukenoefeningen op te lossen. Hierdoor zul je het concept breuk zelf beter begrijpen.
Oefening 1
Bereken de irreducibele fractie van de volgende reduceerbare fracties. Vergeet niet dat je elke methode kunt gebruiken om breuken te vereenvoudigen. En als u klaar bent met de oefening, kunt u uw resultaten vergelijken met de resultaten die we u in de onderstaande afbeelding laten zien.
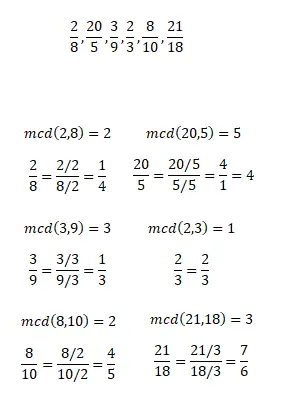
Oefening 2
Identificeer de breuken die gelijkwaardig zijn aan de onherleidbare breuken 2/3 en 4/5. Om deze taak te voltooien, raden we aan om naar de getallen in de teller en de noemer te kijken en na te denken over de deelbaarheidsrelatie die ze hebben. Misschien kun je de grootste gemene deler of het kleinste gemene veelvoud gebruiken om te vinden wat je zoekt...
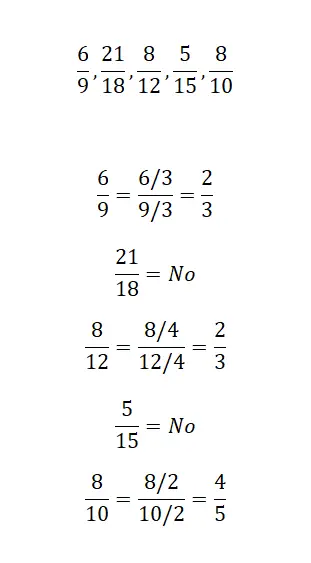
Oefening 3
Bij deze laatste opgave hoef je alleen maar aan te geven of de volgende drie breuken dezelfde onherleidbare breuk hebben. Het is daarom noodzakelijk om de drie fracties zoveel mogelijk te verkleinen en het resultaat te analyseren. Zodra u het heeft opgelost, kunt u uw oplossingen vergelijken met de onze.
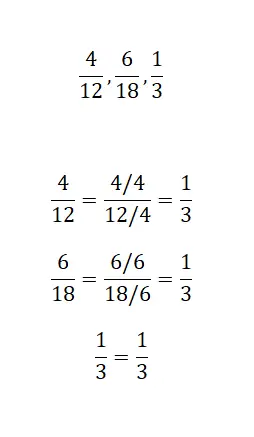
Meer informatie over breuken
We hopen dat dit artikel je heeft geholpen onherleidbare breuken te begrijpen. Als je vragen hebt, lees dan gerust onze uitleg over breuken . Daar vindt u alle informatie over breuken: definitie, categorieën, bewerkingen en oefeningen, allemaal uitgelegd aan de hand van theorie en voorbeelden. Wij verzekeren u dat als u dit artikel leest, u veel fundamentele twijfels met betrekking tot dit onderwerp zult wegnemen.