Breuken of gemengde getallen zijn een zeer belangrijk wiskundig concept op het gebied van calculus. Daarom is het essentieel om te weten hoe ze werken en hoe je breukenoefeningen oplost. Dit is het doel van dit artikel, of je nu leert hoe je bewerkingen met breuken oplost of welke andere vorm van oefening of probleem dan ook waarbij getallen van deze stijl voorkomen. Dat gezegd hebbende, laten we beginnen met de eerste oefeningen.
Oefening op bewerkingen met breuken
Om te beginnen bieden we enkele basisbewerkingen, waaronder breuken. Je hoeft ze alleen maar op te lossen en het vereenvoudigde resultaat uit te drukken. Dus als u klaar bent met het oplossen van de berekeningen , raden wij u aan de resultaten te vergelijken en te kijken naar de correctie die wij u aanbieden. Hoewel u uw resultaten ook kunt controleren met onze online breukencalculator .
Breuken met een gemeenschappelijke noemer optellen en aftrekken
Hieronder heb je twee optellingen en twee aftrekkingen van breuken opgelost, probeer ze zelf op te lossen en vergelijk het resultaat. Op deze manier bekijkt u de oplossingsmechanismen voor dit soort operaties:
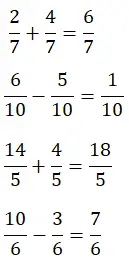
Breuken met verschillende noemers optellen en aftrekken
Nu verhogen we het niveau een beetje, want om het optellen en aftrekken van breuken met verschillende noemers op te lossen, moeten we eerst de lcm van de noemers vinden. De berekening wordt daardoor iets ingewikkelder.
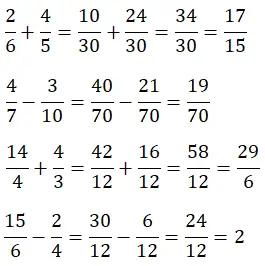
Breuken vermenigvuldigen en delen
In dit gedeelte moet je het vermenigvuldigen en delen van breuken oplossen. Deze bewerkingen zijn heel gemakkelijk uit te voeren, maar je moet ze nog steeds oefenen. Net als in de vorige twee secties heb je er twee van elk type.
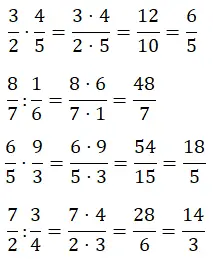
gecombineerde breuken
Ten slotte zul je gecombineerde breuken moeten oplossen, dit zijn bewerkingen gecombineerd met breuken. Het meest ingewikkelde onderdeel hiervan is de berekening, aangezien je al je kennis over bewerkingen met gemengde getallen moet verzamelen om een dergelijke berekening correct te kunnen oplossen.

Oefening in conversies tussen decimalen en breuken
Probeer nu de volgende decimale getallen om te zetten in een genererende breuk en omgekeerd. Om dit correct te doen, moet u echter rekening houden met het type decimaalteken (exact, puur periodiek of gemengd periodiek), aangezien de conversiemethoden variëren. Als je deze methoden niet meer weet, raden we je aan ons artikel over breuken te lezen, omdat we daar alle procedures uitleggen voor het converteren tussen decimalen en breuken en omgekeerd. Hieronder vindt u enkele opgeloste conversies, wij raden u aan deze zelf te proberen:

Oefening op gelijkwaardige breuken
Nadat je de basisrekenkunde en conversies hebt geoefend, is het tijd om met equivalente breuken te beginnen. In deze sectie laten we je verschillende breuken zien en moet je de paren gelijkwaardige breuken vinden. Op deze manier oefen je het concept van gelijkwaardigheid en bestudeer je ook vereenvoudigende breuken .

Fractievergelijkingsoefening
Vervolgens laten we u verschillende breuken zien en moet u ze vergelijken met de symbolen “<“, “=” en “>”. Om deze oefening op te lossen, moet je een gemeenschappelijke noemer vinden en beide breuken omzetten naar die noemer. Op deze manier kun je zien welke van de twee tellers groter is, en moet je dienovereenkomstig handelen:

Oefening met breuken op de getallenlijn
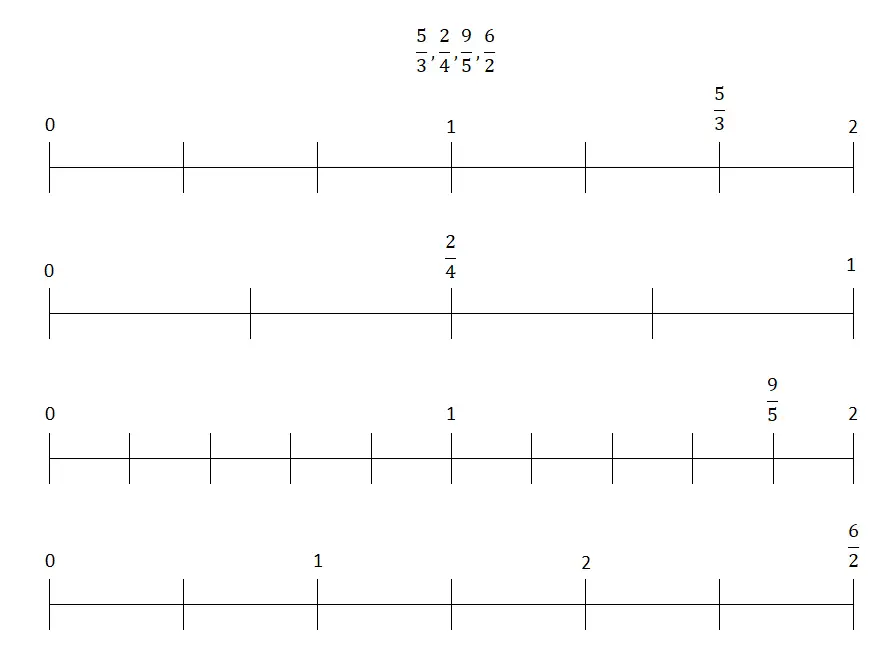
In deze oefening moet je de verschillende breuken die we je gaan geven op een getallenlijn ordenen, dus de oplossingsprocedure kan behoorlijk gevarieerd zijn. U kunt bijvoorbeeld de afstand tussen twee gehele getallen delen door zoveel delen als aangegeven door de waarde van de noemer, en vervolgens de breuk in het segment plaatsen dat wordt aangegeven door de teller .
Bovendien kunt u de teller delen door de noemer en zo een decimaal getal krijgen, dat u later op de lijn plaatst. Hoewel deze tweede procedure veel fundamenteler is, hebben we er daarom voor gekozen om de eerste methode te kiezen die we hebben uitgelegd. Dat gezegd hebbende, de breuken die je aan de rechterkant moet plaatsen, zijn als volgt:
breukproblemen
Ten slotte komen we bij het laatste deel van dit artikel, waarin we enkele breukproblemen zullen behandelen. Hoewel we eerst de juiste procedure willen beschrijven die u moet gebruiken bij het oplossen van wiskundige problemen :
- Begrijp het probleem: De eerste stap is het goed lezen, waardoor je het hele probleem begrijpt. Zo maakt u kennis met alle informatie die in de aangifte wordt uitgelegd. Als je dit onderdeel correct uitvoert, heb je veel bereikt, omdat je weet hoe je de oplossing en alle berekeningen moet routeren.
- Probleemstelling: Zodra u weet wat het probleem is, moet u het presenteren. U kunt dit doen met behulp van een diagram, tekening of kleine grafische weergave van de gegevens. In deze stap ga je nadenken over manieren om de gegevens met elkaar te verbinden en het probleem op te lossen.
- Los het probleem zelf op: Later kun je doorgaan met het numeriek oplossen van het probleem, in deze fase moet je de theorieën testen die je in de vorige sectie naar voren hebt gebracht. Dit is waar je daadwerkelijk een actieplan uitvoert en de resultaten behaalt, dus je moet heel gefocust zijn.
- Interpreteer de oplossingen: Als u ten slotte al over de oplossingen beschikt, moet u deze resultaten interpreteren en ze in de context van het probleem begrijpen. Deze laatste stap is erg belangrijk en veel mensen negeren deze, omdat ze denken dat een numeriek resultaat voldoende is, maar in werkelijkheid moet je de oplossing in één zin samenvatten.
probleem 1
Als we een zwembad met één kraan willen vullen duurt het 6 uur, maar als we het met een andere kraan doen duurt het 8 uur. Hoeveel van het zwembad wordt in 2 uur gevuld als we beide kranen tegelijkertijd gebruiken? Druk het resultaat uit als een breuk.
Om dit probleem op te lossen, moeten we breuken gebruiken. Wat we eigenlijk gaan doen, is afzonderlijk berekenen hoeveel elke kraan gedurende die twee uur zal vullen. De eerste kraan vult dus 1/6 van de tank in één uur en als we dit met twee uur vermenigvuldigen, wordt 2/6 gevuld. Terwijl de tweede kraan binnen een uur 1/8 zal vullen en we het ook met 2 zullen moeten vermenigvuldigen, waarmee we 2/8 zullen hebben.
Ten slotte zullen we de twee breuken bij elkaar optellen om het totale bedrag van de pool te verkrijgen dat gevuld zal zijn. We houden dus 2/6 + 2/8 = 7/12 van de pool over.
probleem 2
We hebben 64 snoepjes, maar we geven 1/4 daarvan aan onze vriend Marcos. Daarna eten we 3 snoepjes en geven 2/5 van het resterende bedrag aan onze vriendin María. Hoeveel snoep hebben we nog? Druk het uit als een geheel getal.
Eerst moeten we een kwart aftrekken van het totale aantal van 64, daarna trekken we 3 af van het verkregen resultaat en ten slotte trekken we twee vijfde van deze hoeveelheid snoep af. Hiermee kunnen we dit berekenen met gecombineerde breuken:
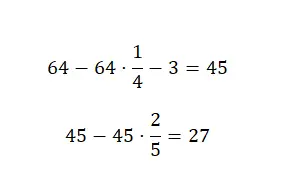
Daarom houden we aan het einde 27 snoepjes over.
probleem 3
We hebben een perceel grond van 10.000 m² verdeeld in drie ongelijke delen. Het eerste deel vertegenwoordigt 3/6 van de totale oppervlakte en het tweede deel is gelijk aan de helft van het vorige. Welke breuk beschrijft de oppervlakte van het derde gedeelte? Hoeveel vierkante meter heeft elke sector?
Het eerste wat we gaan doen is de breuk van het derde diagram berekenen, dit doen we door middel van een heel eenvoudige aftrekking van breuken. Vervolgens berekenen we de oppervlakte van elke sectie door de fractie van een getal te berekenen, in ons geval is deze numerieke waarde 10.000. Hieronder ziet u de hele procedure: