Eerstegraadsvergelijkingen of lineaire vergelijkingen vormen de basis van de algebra , want als je ze niet begrijpt, zal het heel moeilijk voor je zijn om complexere vergelijkingen te begrijpen. Het bijzondere van dit soort vergelijkingen is dus dat het letterlijke deel van de monomialen geen exponent kan hebben. Daarom vinden we in een lineaire vergelijking alleen monomialen zonder letterlijk deel en monomialen met een letterlijk deel zonder exponent, zoals: 3 + x = -5 – 3x .
Merk ook op dat deze vergelijkingen meestal een unieke oplossing hebben, ook al is dat mogelijk niet het geval. Om te weten welk geval we voor ons hebben, moeten we de vergelijking oplossen en uiteindelijk het resultaat analyseren . Dus als we een onmogelijke gelijkheid verkrijgen, zoals 2 = 0, dan heeft de vergelijking geen oplossing. Aan de andere kant, als we een gelijkheid verkrijgen die altijd waar is, dan is de oplossing gelijk aan alle reële getallen. En ten slotte, als we aan het einde de gelijkheid van X en een numerieke waarde verkrijgen, zullen we in dit geval een uniek resultaat hebben.
Procedure voor het oplossen van een lineaire vergelijking
Het oplossen van een vergelijking komt overeen met het berekenen van de waarde van een variabele, weergegeven door een letter (x, y, a, b…). Om deze waarde te vinden, moeten we dus de volgende stappen volgen:
- Haakjes en breuken oplossen: Om te beginnen verwijderen we alle haakjes en noemers, om een vergelijking te krijgen die gemakkelijker te begrijpen is. Omdat we direct kunnen waarderen welke termen gepaard gaan met het onbekende en welke niet, stelt deze lezing ons in staat de uitdrukking gemakkelijk verder op te lossen.
- Laten we de uitdrukking vereenvoudigen: we groeperen vergelijkbare termen (onafhankelijke termen aan de ene kant en termen met x aan de andere kant). Dus aan de ene kant laten we de nummers met het onbekende achter en geven we de andere nummers door aan de andere kant. Maar onthoud: om hun kant te veranderen, moeten we hun teken veranderen.
- Werk aan elke kant: We voeren alle bewerkingen in de volgende volgorde uit: machten/wortels, vermenigvuldigingen/delingen en optellingen/aftrekkingen. We doen dit totdat we aan elke kant een enkele term krijgen, en zo krijgen we een vergelijking met dezelfde structuur als deze: 4x = 8.
- Isoleer de variabele: geef ten slotte eenvoudigweg de waarde door die bij de letter hoort door deze aan de andere kant te delen en zo vinden we de uiteindelijke waarde ervan. Aan het einde van deze stap hebben we het onbekende opgelost en weten we welk type resultaat er overblijft: een unieke oplossing, een ongeldige oplossing of een oplossing die tevreden is met alle gehele getallen.
Voorbeelden van eerstegraadsvergelijkingen
Hieronder vindt u opgeloste eerstegraadsvergelijkingen , die in verschillende categorieën zijn georganiseerd op basis van de complexiteit van hun structuur. Dus als je de theoretische procedure kent om lineaire vergelijkingen op te lossen en de verschillende soorten die er bestaan, zul je al over de nodige kennis beschikken om ze gemakkelijk op te kunnen lossen en zullen we beginnen met oefenen. Dat gezegd hebbende, laten we beginnen met de theoretische verklaring:
Basisvergelijkingen van de eerste graad
Dit eerste type lineaire vergelijkingen bestaat alleen uit elementaire rekenkundige bewerkingen (optellen, aftrekken, vermenigvuldigen en delen). Hier zijn twee uitgewerkte voorbeelden, de eerste is iets eenvoudiger en de tweede is iets ingewikkelder qua berekening:
-6x + 4 – 1 = 6x -3
-6x + 3 = 6x – 3
-6x – 6x = -3 – 3
-12x = -6
x = 1 / 2
-24x – 3 + 4x = -4x – 27
-20x – 3 = -4x – 27
-20x + 4x = -27 + 3
-16x = -24
x = 3 / 2
Eerstegraadsvergelijkingen met haakjes
Ten tweede hebben we de lineaire vergelijkingen tussen haakjes. Deze zijn iets ingewikkelder om op te lossen dan de vorige, hoewel hun enige moeilijkheid in de berekening ligt, aangezien de eigenschappen van de haakjes moeten worden gerespecteerd. Om het duidelijker te maken, laten we u twee uitgewerkte voorbeelden zien:
2(x + 3) – 4x = -4
2x + 6 – 4x = -4
-2x = -10
x = 5
-2 + 3 (4x + 5) = -1 (x + 2) + 2 (-3x + 2)
-2 + 12x + 15 = -x – 2 – 6x + 4
13 + 12x = -7x + 2
12x + 7x = -13 + 2
19x = -11
x = -11 / 19
Eerstegraadsvergelijkingen met machten en wortels
Het derde niveau is vrij eenvoudig, omdat het alleen maar krachten en wortels toevoegt. De enige moeilijkheid die je tegen kunt komen met deze vergelijkingen is wanneer de exponent of wortel een haakje met gehele getallen beïnvloedt (zoals het tweede voorbeeld dat we je laten zien), maar al het andere blijft vrijwel hetzelfde. Hieronder staan twee voorbeelden.
3² + √25 – 2x = 2³x + 4
9 + 5 – 2x = 8x + 4
14 – 2x = 8x + 4
-2x – 8x = -14 + 4
-10x = -10
x = 1
4x + (2 – 1 +5)² = 3x – √16
4x + 6² = 3x – 4
4x – 3x = -4 -36
x = -40
Eerstegraadsvergelijkingen met breuken
De laatste categorie lineaire vergelijkingen die we kunnen vinden is deze, die is samengesteld uit alle elementen waar we eerder commentaar op hebben gegeven, en ook uit breuken. Dit niveau is het meest complex en er zijn verschillende methoden om ze op te lossen. De eerste en eenvoudigste is om de noemers te vermenigvuldigen met de tegenovergestelde kant van de gelijkheid, hoewel we dit alleen kunnen gebruiken als we twee breuken hebben. Aan de andere kant, als we meer dan twee breuken in de vergelijking hebben, moeten we een gemeenschappelijke noemer vinden en alle breuken vermenigvuldigen door die waarde te delen door de noemer van dezelfde breuk. Hieronder ziet u een voorbeeld van elk type:
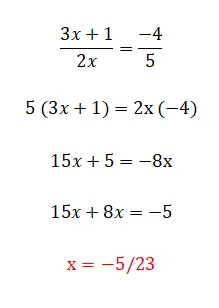
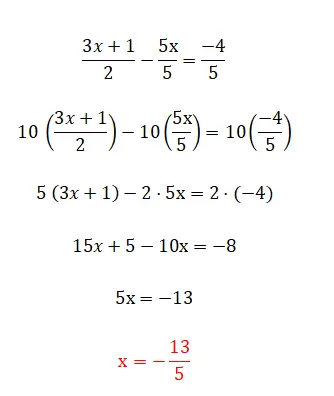
Oefeningen op eerstegraadsvergelijkingen
Nu bieden we enkele lineaire vergelijkingsoefeningen aan. Ze zijn georganiseerd volgens toenemende moeilijkheidsgraad, waarbij de eerste vergelijkingen eenvoudiger zijn dan de laatste. Daarom raden wij u aan om bij het begin te beginnen en te kijken hoe ver u kunt komen. Probeer dus de volgende vergelijkingen op te lossen en vergelijk vervolgens uw resultaat met de oplossingen die wij bieden.
Eerste oefening
De eerste oefening is een heel eenvoudige lineaire vergelijking, omdat deze alleen uit optellingen en aftrekkingen bestaat, en er ook maar vier termen zijn tussen de twee zijden van de gelijkheid:
2x – 3 = 4x + 5
2x – 4x = 5 + 3
-2x = 8
x = 8 / (-2)
x = -4
- We groeperen vergelijkbare termen bij elkaar.
- We vereenvoudigen beide kanten.
- We wissen het onbekende en berekenen de waarde ervan.
tweede oefening
In dit geval bevinden we ons met een vergelijking gevormd door haakjes, waarbij het onze topprioriteit is om ze te elimineren, zodat we vervolgens soortgelijke termen kunnen groeperen:
-4(x + 2) + 5x = 6 + 5x
-4x – 8 + 5x = 6 + 5x
-4x + 5x – 5x = 6 + 8
-4x = 14
x = 14 / (-4) = -7 / 2
- We lossen de haakjes op.
- We verplaatsen de x-en naar links en de onafhankelijke termen naar rechts.
- Wij verhelderen het onbekende.
We vereenvoudigen het resultaat.
derde oefening
Vervolgens moet je nog een kwadratische vergelijking tussen haakjes oplossen, hoewel deze iets moeilijker is. Dit komt omdat er geneste haakjes in staan (haakjes tussen andere haakjes). Daarom moet u de volgorde van oplossing correct volgen: eerst insiders, dan outsiders.
3x + 2 (x – (4x – 5)) = 1 – (3 (2x + 7) – 2)
3x + 2 (x – 4x + 5) = 1 – (6x + 21 – 2)
3x + 2x – 8x + 10 = 1 – 6x – 21 + 2
-3x + 10 = -6x – 18
3x = -28
x = -28 / 3
- We beginnen met het oplossen van de binnenste haakjes.
- Vervolgens lossen we de buitenste haakjes op.
- We vereenvoudigen beide kanten van de gelijkheid en verzamelen vergelijkbare termen.
- We isoleren x en berekenen de waarde ervan.
vierde oefening
In deze oefening beginnen we breuken te zien, die waarschijnlijk het meest gecompliceerde element van lineaire vergelijkingen zijn. Maar maak je geen zorgen, want als je de theorie hebt gelezen, weet je perfect hoe je het moet doen:
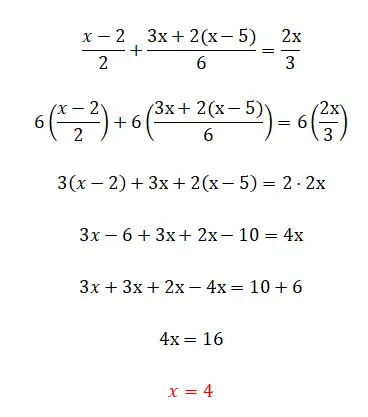
Vijfde oefening
In deze vijfde oefening zien we breuken tussen haakjes, wat betekent dat de oplossingshiërarchie een beetje ingewikkeld wordt. Het is de moeite waard te vermelden dat dit voorbeeld kan worden opgelost met behulp van twee methoden: met behulp van de methode van de kleinste gemene veelvouden of door rechtstreeks met breuken te werken. Hieronder ziet u de twee volledige procedures:
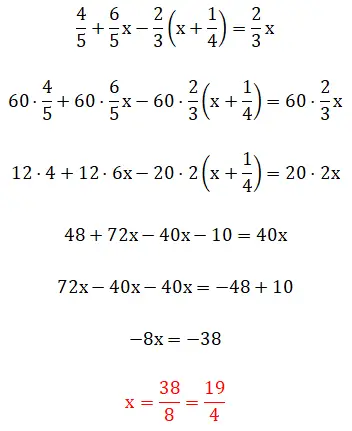
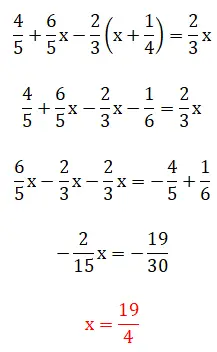
zesde oefening
Vervolgens gaan we iets verder met het onderwerp breuken en haakjes, aangezien we haakjes hebben genest. Deze oefening brengt niet veel meer complicaties met zich mee vergeleken met de vorige, het is gewoon iets moeilijker qua berekeningen en dat is alles.
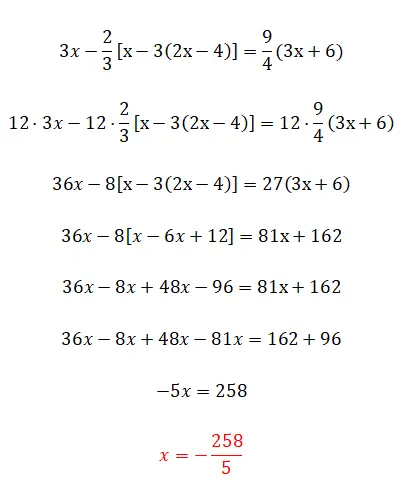
- We vermenigvuldigen alle termen met de lcmp van de noemers.
- We vereenvoudigen de uitdrukking door de haakjes te verwijderen: eerst de haakjes binnen en dan de buitenhaakjes.
- We groeperen soortgelijke termen aan elke kant.
- We lossen de operaties aan elke kant op.
- En we berekenen de waarde van het onbekende.
zevende oefening
De volgende oefening lijkt misschien heel eenvoudig, maar we raden u aan deze toch te proberen op te lossen, omdat dit zeker een enigszins ongebruikelijk resultaat zal opleveren. Nadat je het geprobeerd hebt, bekijk je de oplossing en uitleg onder de oefening.
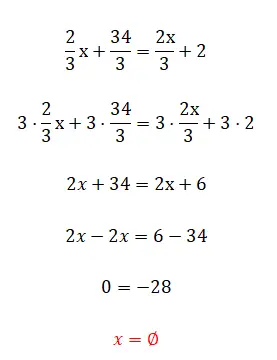
- We vermenigvuldigen alle breuken met de lcm van de noemers.
- We vereenvoudigen de verkregen uitdrukking.
- En uiteindelijk zien we dat het ons een valse gelijkheid geeft, omdat we het onbekende hebben geëlimineerd.
Zoals je misschien hebt gemerkt, is dit een valse gelijkheid of een gelijkheid zonder resultaat, omdat er geen waarde is die de vergelijking correct aanvult. Dit is een van de gevallen die we in de inleiding noemden.
achtste oefening
Ten slotte bieden we je deze oefening aan, die behoorlijk ingewikkeld is omdat deze alle complicaties bevat die we in dit artikel hebben gezien, maar er zit ook een klein trucje in. Zeg dat als je deze eerstegraadsvergelijking kunt oplossen, je de hele theorie perfect hebt begrepen. En zo niet, maak je geen zorgen, want deze oefening is behoorlijk ingewikkeld.
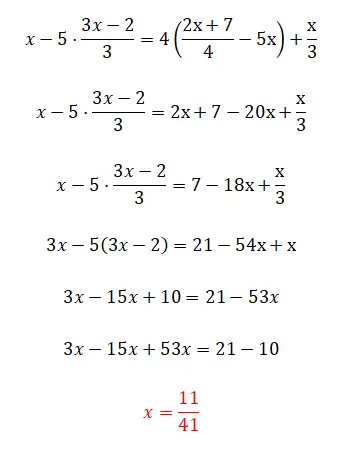
- We beginnen met het elimineren van de vier aan de rechterkant van de vergelijking.
- Dan voegen we de x’s aan de rechterkant samen.
- We vermenigvuldigen alle termen met drie, om de noemers te elimineren.
- We verwijderen de haakjes.
- We hebben soortgelijke termen bij elkaar gezet.
- We berekenen de waarde van het onbekende.
Meer lineaire vergelijkingsoefeningen
Nu je genoeg oefening hebt gehad, zou je complexe lineaire vergelijkingen moeten kunnen oplossen . Maar als je wilt blijven oefenen, raden we je aan dit werkblad op te lossen. Maar als u denkt dat u voldoende heeft besproken, kunnen we u ook een artikel aanbieden dat u kan helpen de hiërarchie van bewerkingen te begrijpen. Zo weet je altijd welke berekening je als eerste moet oplossen en maak je nooit een fout .